MATLAB回归分析的异常值处理：专家级别的检测与对策

# 1. 回归分析基础与异常值概述

## 引言
回归分析作为统计学中的一种重要工具，广泛应用于数据分析领域。它能够通过确定变量之间的关系，进行预测、建模和解释数据。然而，在实际应用中，数据集可能受到异常值的影响，导致回归分析的结果产生偏差。

## 回归分析简介
回归分析的目的是评估和量化变量之间的关系。常见的回归类型包括简单线性回归和多元线性回归。在进行回归分析时，选择合适的模型以及理解变量间的关系至关重要。

## 异常值的影响
异常值，或称为离群点，是指在数据集中显著偏离其他观测值的数据点。这些离群点可能是由于错误或极端事件引起的，它们对回归分析的准确性有着显著影响。在数据预处理阶段识别并处理异常值，对于获得准确的回归分析结果至关重要。

要进行有效的异常值检测和处理，我们将进一步探讨异常值的理论基础、检测方法以及如何在MATLAB中应用这些理论和方法。

# 2. 异常值的理论基础与检测方法

## 2.1 异常值的定义和影响

异常值，也称为离群点，是指在数据集中显著偏离其他观测值的点。它可能是由于测量误差、数据录入错误或真实的但罕见的现象造成的。识别和处理异常值对于数据分析和建模至关重要，因为它们可能会扭曲统计分析的结果，导致误导性的结论。

### 2.1.1 异常值在数据集中的表现形式

异常值可能以多种形式出现在数据集中，例如：

- 单一的孤立点，与其他数据点有明显的差异。
- 成簇的异常值，这些点在某些特征上与其他数据点保持一致，但整体上与主体数据集不同。
- 穿插在正常数据中的小规模异常点，它们可以是由噪声引起的微小偏差。

识别异常值通常涉及可视化技术，如散点图、箱形图以及统计技术，比如标准差和四分位距等。

### 2.1.2 异常值对回归分析的影响

异常值对回归分析的影响可以从以下几个方面来理解：

- **估计的偏差**：异常值可能会导致回归线显著偏离大部分数据点，从而使得斜率和截距等参数的估计产生偏差。
- **预测误差增大**：异常值会使得残差平方和增大，进而增加预测误差。
- **系数的不稳定性**：如果数据集中包含异常值，那么回归模型的系数可能会非常不稳定，尤其是在使用最小二乘法估计参数时。

理解异常值的影响有助于我们采取恰当的处理策略来减小其对模型的影响。

## 2.2 统计学中的异常值检测方法

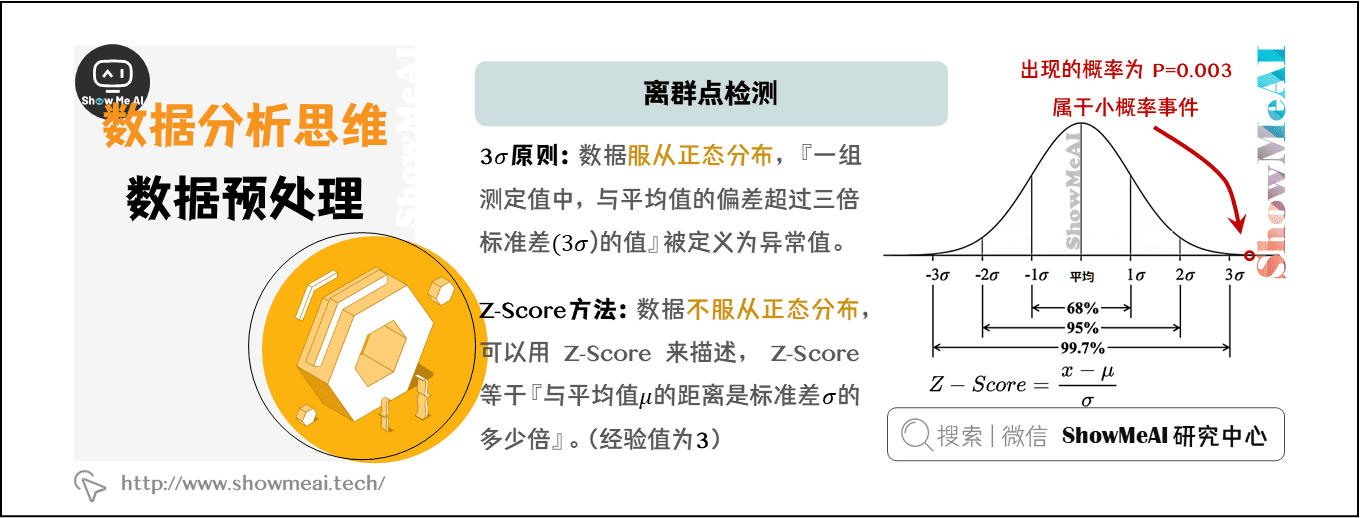
### 2.2.1 基于标准差的方法

利用标准差进行异常值检测是一种简单但有效的方法，它依据数据分布的统计特性来识别离群点。以下是一个基本步骤：

1. 计算数据集的均值（mean）和标准差（standard deviation, SD）。
2. 设定一个阈值，通常为3倍标准差。
3. 任何距离均值超过3倍标准差的点被认为是异常值。

这种方法假设数据是正态分布的，对于非正态分布的数据，需要使用更复杂的方法。

### 2.2.2 基于四分位距的方法

四分位距（Interquartile Range, IQR）是第三四分位数（Q3）和第一四分位数（Q1）之间的差值，用于衡量数据的离散程度。

1. 计算Q1、Q3和IQR。
2. 计算数据的上下界，分别为：Q1 - 1.5 * IQR 和 Q3 + 1.5 * IQR。
3. 落在上下界之外的数据点被认为是异常值。

这种方法的优点在于它不依赖于数据分布的形状，从而更适用于偏态分布。

### 2.2.3 基于局部异常因子（LOF）的方法

局部异常因子（Local Outlier Factor, LOF）是一种基于密度的异常值检测方法。与传统方法不同，LOF 不需要指定一个阈值。它通过比较给定数据点的局部密度与邻居点的局部密度来识别异常值。

LOF 值大于1通常意味着一个点比其周围环境更稀疏，因此可能是一个异常值。LOF 方法对于检测成簇的异常值特别有效。

## 2.3 可视化工具在异常值检测中的应用

### 2.3.1 散点图和箱形图的使用

- **散点图**：可视化数据点的分布，通过观察散点图可以直观地看出数据中的异常值。
- **箱形图**：展示数据的四分位数分布和异常值。箱体上下边界表示Q1和Q3，而异常值则显示为单独的点。

箱形图是识别异常值的直观工具，但有时需要结合散点图进行详细分析。

### 2.3.2 其他数据可视化技巧

其他一些有用的可视化方法包括：

- **小提琴图**：结合箱形图和密度图的特性，提供关于数据分布的信息。
- **热图**：在高维数据中识别异常值，可以通过颜色的深浅反映数据点的密度或异常程度。
- **马赛克图**：一种用于展示多项式回归的图示方法，可以用来识别回归中的异常值。

这些可视化技术有助于提供对数据更深入的理解，从而在检测和理解异常值时发挥作用。

# 3. MATLAB在回归分析中的应用

回归分析是统计学中用于预测和控制变量间关系的一种重要工具。在众多的统计软件中，MATLAB凭借其强大的数值计算能力和直观的图形用户界面（GUI），成为研究人员和工程师进行数据分析的首选平台之一。本章节将详细介绍MATLAB在回归分析中的应用，包括基础使用、数据分析函数的运用，以及如何通过GUI提升分析的互动性和效率。

## 3.1 MATLAB回归分析基础

### 3.1.1 MATLAB回归分析工具箱介绍

MATLAB为回归分析提供了内置的工具箱，即Statistics and Machine Learning Toolbox。该工具箱包含了一系列的函数和应用程序，用于拟合、验证和评价回归模型。除了线性回归，该工具箱还支持多种类型的回归，如逻辑回归、岭回归、LASSO回归等。工具箱中的函数通常只需要输入特征变量和响应变量即可进行回归分析，非常适合快速的建模和预测。

### 3.1.2 构建基本的回归模型

在MATLAB中构建回归模型的基本步骤包括数据准备、模型拟合、模型评估和预测。以下是一个使用MATLAB进行线性回归的简单示例：

% 加载数据
load carsmall

% 选择特征和响应变量
X = [Weight, Model_Year]; % 特征变量
y = MPG; % 响应变量

% 拟合线性回归模型
mdl = fitlm(X, y);

% 查看模型摘要
disp(mdl)

在上述代码中，`fitlm` 函数用于拟合线性回归模型。该函数返回一个`LinearModel`对象，包含模型的详细信息，如回归系数、统计显著性、R²值等。通过查看模型摘要，我们可以评估模型的质量和拟合度。

## 3.2 MATLAB中的数据分析函数

### 3.2.1 数据预处理与分析函数

在进行回归分析之前，数据预处理是一个不可忽视的步骤。MATLAB提供了众多函数用于数据清洗、标准化和转换。例如：

% 数据标准化
X = zscore(X);

% 数据插补
% 假设有一个缺失值，使用平均值进行插补
X(isnan(X)) = mean(X, 'omitnan');

在上述代码中，`zscore` 函数用于对数据进行标准化处理，即将数据转换为均值为0，标准差为1的形式，这有助于消除不同量纲和数量级的影响。`isnan` 函数用于检测数据中的缺失值，`mean` 函数则用于计算均值。

### 3.2.2 回归分析专用函数及用法

MATLAB的统计工具箱不仅提供了`fitlm`函数用于线性回归，还提供了其他针对不同需求的回归分析函数。例如，对于逻辑回归可以使用`fitglm`函数：

% 假设有一个二元分类目标变量
y_binary = logical(y > median(y));

% 拟合逻辑回归模型
mdl_glm = fitglm(X, y_binary, 'Distribution', 'binomial');

在这个示例中，`fitglm`函数用于拟合逻辑回归模型，其中`'Distribution'`参数设置为`'binomial'`，表示我们进行的是二项分布的逻辑回归。这种方法常用于分类问