常见Python算法的复杂度比较：排序、搜索和递归的效率对比

# 1. Python算法概述及复杂度基础

## 1.1 算法与Python的关系
Python，作为一种多范式编程语言，因其简洁清晰的语法和强大的标准库，常被用来实现各类算法。在数据处理、人工智能、网络爬虫等IT领域，Python算法的应用几乎无处不在，其背后的复杂度分析对于优化代码性能至关重要。

## 1.2 复杂度分析的重要性
算法效率的评估主要依赖于时间复杂度和空间复杂度的分析。时间复杂度反映了算法执行时间与输入数据量之间的关系，而空间复杂度则反映了算法在执行过程中占用的存储空间大小。深入理解复杂度，可以帮助程序员在面对不同规模数据时，作出更合理的算法选择。

## 1.3 时间复杂度与空间复杂度
时间复杂度通常用大O表示法来描述，如O(n)、O(n^2)等。空间复杂度同理，描述算法占用内存空间的量级。在Python中，高效的算法往往需要平衡二者，以达到最佳的性能表现。例如，对于大数据集，一个O(nlogn)的排序算法可能比O(n^2)的排序算法更适合，即使它们的空间复杂度相同。

# 示例：一个简单的冒泡排序算法，具有O(n^2)的时间复杂度
def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr

在本章中，我们将深入探讨算法在Python中的实现方式以及如何进行复杂度分析。通过理解这些基本概念，读者将为深入学习后续章节的排序、搜索、递归算法打下坚实的基础。

# 2. 排序算法的理论与效率分析

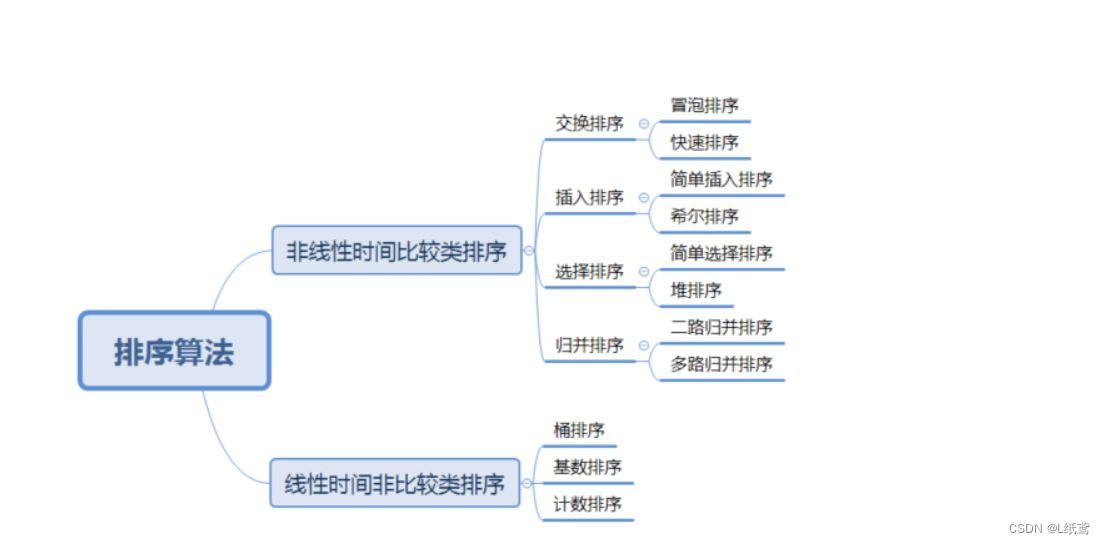
## 2.1 常见排序算法概述

排序算法是计算机科学中最基本的概念之一，它的目的是将一系列的数据按照一定的顺序排列。本小节将概述几种常见的排序算法，并分析它们的优缺点和使用场景。

### 2.1.1 冒泡排序与选择排序

冒泡排序（Bubble Sort）是一种简单的排序算法，它重复地遍历待排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复进行直到没有再需要交换，也就是说该数列已经排序完成。

选择排序（Selection Sort）的工作原理和冒泡排序类似。选择排序算法是一种原址比较排序算法。工作原理是首先在未排序序列中找到最小（或最大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（或最大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr

def selection_sort(arr):
    n = len(arr)
    for i in range(n):
        min_idx = i
        for j in range(i+1, n):
            if arr[j] < arr[min_idx]:
                min_idx = j
        arr[i], arr[min_idx] = arr[min_idx], arr[i]
    return arr

以上代码展示了冒泡排序和选择排序的实现。`bubble_sort`函数通过两层嵌套循环完成排序，而`selection_sort`函数则是通过寻找最小元素的方式来实现排序。

### 2.1.2 插入排序与快速排序

插入排序（Insertion Sort）的工作方式类似于我们在玩扑克牌时整理牌的方式。从第一个元素开始，该算法将这个元素视为一个已经排好序的序列。随后，从第二个元素开始，逐个向已排序序列中插入新的元素，同时保持已排序序列的有序性。

快速排序（Quick Sort）则是一种分而治之的排序方法。它采用递归的方式进行排序。首先，从数列中选取一个数作为"基准"（pivot）。然后，将所有比这个数小的数都放到它的左边，比它大的数都放到右边，然后递归地对左右两边的子序列进行快速排序。

def insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i-1
        while j >=0 and key < arr[j]:
            arr[j+1] = arr[j]
            j -= 1
        arr[j+1] = key
    return arr

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

在以上代码中，`insertion_sort`函数通过插入的方式进行排序，而`quick_sort`函数则是通过递归调用，将数组分成更小的部分来进行排序。

## 2.2 排序算法的时间复杂度比较

在比较排序算法的效率时，我们通常会考虑时间复杂度。时间复杂度是对算法运行时间的度量，它与输入数据的大小有关。复杂度分析通常分为最佳、平均和最坏情况三种。

### 2.2.1 最佳、平均和最坏情况分析

最佳情况发生在输入数组已经是排序好的情况下，而最坏情况则是输入数组是反向排序的。平均情况通常指的是算法在随机输入数据上的表现。复杂度的表示方式通常有大O表示法、大Ω（Omega）表示法和大Θ（Theta）表示法。

以下是几种排序算法在不同情况下的时间复杂度：

| 排序算法 | 最佳情况 | 平均情况 | 最坏情况 |
|-----------|----------|----------|----------|
| 冒泡排序 | O(n) | O(n^2) | O(n^2) |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) |
| 插入排序 | O(n) | O(n^2) | O(n^2) |
| 快速排序 | O(n log n)| O(n log n)| O(n^2) |

### 2.2.2 稳定性对排序算法的影响

稳定性是排序算法的另一个重要特性，指的是相等的元素在排序前后是否保持相对顺序不变。例如，对于等值元素A和B，如果在排序后的结果中，A仍然在B之前，则该排序算法是稳定的。冒泡排序和插入排序是稳定的排序算法，而快速排序则是不稳定的。

## 2.3 排序算法的空间复杂度分析

空间复杂度是指在执行算法过程中所需的存储空间大小。空间复杂度与时间复杂度一起，是衡量算法优劣的重要标准。

### 2.3.1 原地排序与非原地排序的比较