二分搜索的复杂度深入分析：极致优化与应用场景

# 1. 二分搜索算法概述

二分搜索算法，也称为折半搜索算法，是一种在有序数组中查找特定元素的高效算法。该算法将有序数组分成两半，首先与中间元素进行比较，根据比较结果，确定目标值是在中间元素的左半部分还是右半部分，然后对选定的一半再次进行二分搜索，直到找到目标值或搜索范围为空。

这个算法的基本思想很简单，但是在实际应用中却非常强大。二分搜索不仅可以减少搜索范围，还能极大地提高搜索效率，其核心在于利用数组的有序性，通过排除法逐步缩小目标值可能出现的区间。

接下来，我们将深入探讨二分搜索算法的理论基础，包括其原理和变体，以及如何在不同场景下进行优化和应用。通过了解和掌握二分搜索算法，你将能够更高效地处理数据搜索问题，并在算法竞赛和实际编程中展现出色的性能。

# 2. 二分搜索算法的理论基础

## 2.1 二分搜索原理

### 2.1.1 搜索过程的数学模型

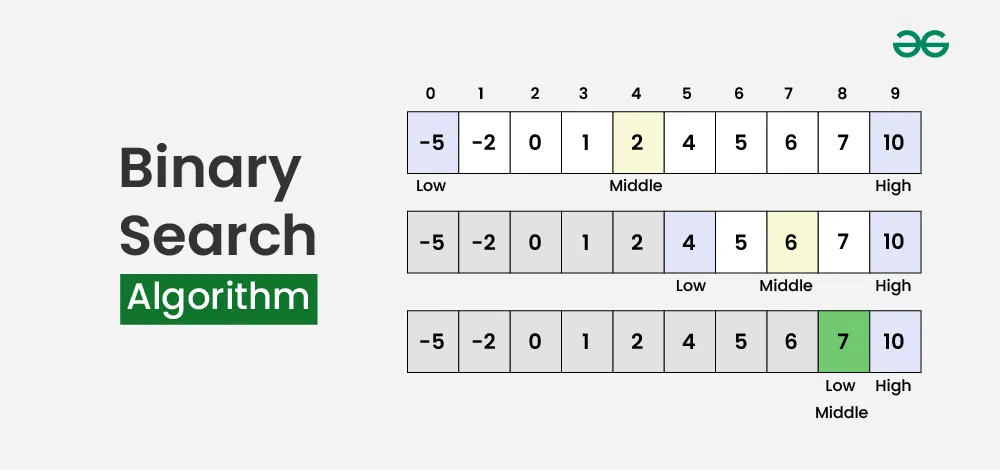
二分搜索，也称为折半查找，是一种在有序数组中查找特定元素的搜索算法。其基本思想是将数组分为两半，比较中间元素与目标值的大小，以决定继续在左半部分还是右半部分查找，从而逐步缩小搜索范围。数学模型可以抽象为以下递归公式：

Search(A, left, right, x):
    if left > right:
        return "Not Found"
    mid = left + (right - left) // 2
    if A[mid] == x:
        return mid
    elif A[mid] < x:
        return Search(A, mid + 1, right, x)
    else:
        return Search(A, left, mid - 1, x)

这里`A`代表有序数组，`left`和`right`分别是数组中的搜索边界，`x`是要搜索的目标值。`mid`是当前搜索区间的中点。

### 2.1.2 时间复杂度分析

二分搜索的时间复杂度为`O(log n)`，其中`n`是数组的元素数量。这个时间复杂度是通过递归树的深度来决定的。每次比较都将搜索区间减半，因此树的深度为`log₂n`。每一次比较可以看作是树的一层，所以二分搜索可以在`O(log n)`的时间内完成。

## 2.2 算法的变体与优化

### 2.2.1 非递归实现

递归实现虽然简洁，但是在某些情况下可能会因为调用栈过大而造成效率低下。非递归实现是另一种常见的实现方式。通过循环来模拟递归过程，这样就可以避免递归调用的开销，代码如下：

def binary_search_non_recursive(arr, x):
    left, right = 0, len(arr) - 1
    while left <= right:
        mid = left + (right - left) // 2
        if arr[mid] == x:
            return mid
        elif arr[mid] < x:
            left = mid + 1
        else:
            right = mid - 1
    return "Not Found"

通过非递归实现，我们将一个递归算法转换为了迭代算法，有效地控制了空间复杂度。

### 2.2.2 搜索边界的处理技巧

二分搜索的一个关键点是处理搜索边界。在某些变体中，比如查找第一个和最后一个出现的元素，处理边界条件是实现的关键。基本的二分搜索在找到目标值后通常会停止，但在查找元素的首次和最终出现时，则需要根据实际问题调整搜索边界。例如，当我们找到一个目标值后，可能需要继续向左查找以找到第一个出现的元素。

### 2.2.3 无限序列中的二分搜索实现

在面对无限序列时，二分搜索依旧适用，但实现会有所不同。在这种情况下，无法一次性获得整个序列的大小，因此无法直接计算出中间点。解决这个问题的一个方法是通过估算数组的大小，或者逐步增大搜索范围，直到找到目标值。具体实现时需要根据实际情况设计循环条件和边界更新的逻辑。

# 3. 二分搜索的实践应用

## 3.1 基本二分搜索的应用实现

### 3.1.1 标准数组中的搜索实现

二分搜索是解决有序集合中查找问题的经典算法。在标准数组中的实现，是将一个有序数组视为搜索的目标空间。二分搜索算法逐步缩小搜索范围，直到找到目标值或者确定目标值不存在为止。

下面是标准数组二分搜索的伪代码实现：

def binary_search(array, target):
    left, right = 0, len(array) - 1
    while left <= right:
        mid = left + (right - left) // 2
        if array[mid] == target:
            return mid
        elif array[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return -1

在此代码块中，我们首先定义了搜索的边界`left`和`right`，这对应于数组的开始和结束索引。然后，通过循环，我们不断计算中间索引`mid`，并根据中间元素和目标值的比较结果来调整搜索范围的边界。

目标值`target`与中间元素`array[mid]`进行比较，有三种情况：

1. 如果`array[mid]`等于`target`，返回`mid`。
2. 如果`array[mid]`