算法实现中的Delaunay三角剖分：从原理到实践

# 1. Delaunay三角剖分的理论基础

Delaunay三角剖分是一种空间划分技术，它将一个点集划分为一系列不相交的三角形，使得每个三角形的外接圆不包含任何其他点。Delaunay三角剖分在计算机图形学、地理信息系统和计算物理学等领域有着广泛的应用。

Delaunay三角剖分的一个重要性质是，它可以最大化点集的最小外接圆半径。这意味着，对于给定的点集，Delaunay三角剖分产生的三角形的外接圆半径是最小的。这个性质对于许多应用非常有用，例如在计算机图形学中用于生成平滑的三维模型。

# 2. Delaunay三角剖分的算法实现

Delaunay三角剖分算法是将一组点集划分为一系列不重叠的三角形，使得每个三角形的外接圆不包含其他点。该算法在计算机图形学、地理信息系统和计算物理学等领域有着广泛的应用。

### 2.1 增量式Delaunay三角剖分算法

#### 2.1.1 算法原理

增量式Delaunay三角剖分算法是一种逐点插入的算法。它从一个空的三角剖分开始，然后逐个插入点，并更新三角剖分以保持Delaunay性质。

#### 2.1.2 算法步骤

1. 初始化一个空的三角剖分。
2. 对于每个点 `p`：
- 找到包含 `p` 的三角形 `T`。
- 将 `p` 插入到 `T` 中，形成三个新的三角形 `T1`、`T2` 和 `T3`。
- 检查 `T1`、`T2` 和 `T3` 是否满足Delaunay性质。如果满足，则继续。否则，执行以下步骤：
- 找到 `T1`、`T2` 和 `T3` 的外接圆。
- 找到外接圆内包含其他点的三角形 `T4`。
- 删除 `T1`、`T2`、`T3` 和 `T4`。
- 重新三角剖分外接圆内的点。

### 2.2 分治法Delaunay三角剖分算法

#### 2.2.1 算法原理

分治法Delaunay三角剖分算法将点集递归地划分为更小的子集，然后对每个子集进行Delaunay三角剖分。最后，将子集的三角剖分合并起来形成整个点集的三角剖分。

#### 2.2.2 算法步骤

1. 如果点集包含少于一定数量的点，则直接使用增量式算法进行三角剖分。
2. 否则，将点集沿最长边进行划分，形成两个子集。
3. 递归地对每个子集进行三角剖分。
4. 合并两个子集的三角剖分，形成整个点集的三角剖分。

### 2.3 随机Delaunay三角剖分算法

#### 2.3.1 算法原理

随机Delaunay三角剖分算法是一种基于随机采样的算法。它首先随机选择一个点作为种子点，然后逐个选择其他点，并更新三角剖分以保持Delaunay性质。

#### 2.3.2 算法步骤

1. 随机选择一个点 `p` 作为种子点。
2. 初始化一个空的三角剖分，并插入 `p`。
3. 对于每个点 `q`：
- 找到包含 `q` 的三角形 `T`。
- 将 `q` 插入到 `T` 中，形成三个新的三角形 `T1`、`T2` 和 `T3`。
- 检查 `T1`、`T2` 和 `T3` 是否满足Delaunay性质。如果满足，则继续。否则，执行以下步骤：
- 找到 `T1`、`T2` 和 `T3` 的外接圆。
- 随机选择一个外接圆内的点 `r`。
- 删除 `T1`、`T2`、`T3`。
- 重新三角剖分外接圆内的点，并插入 `r`。

# 3.1 地理信息系统中的应用

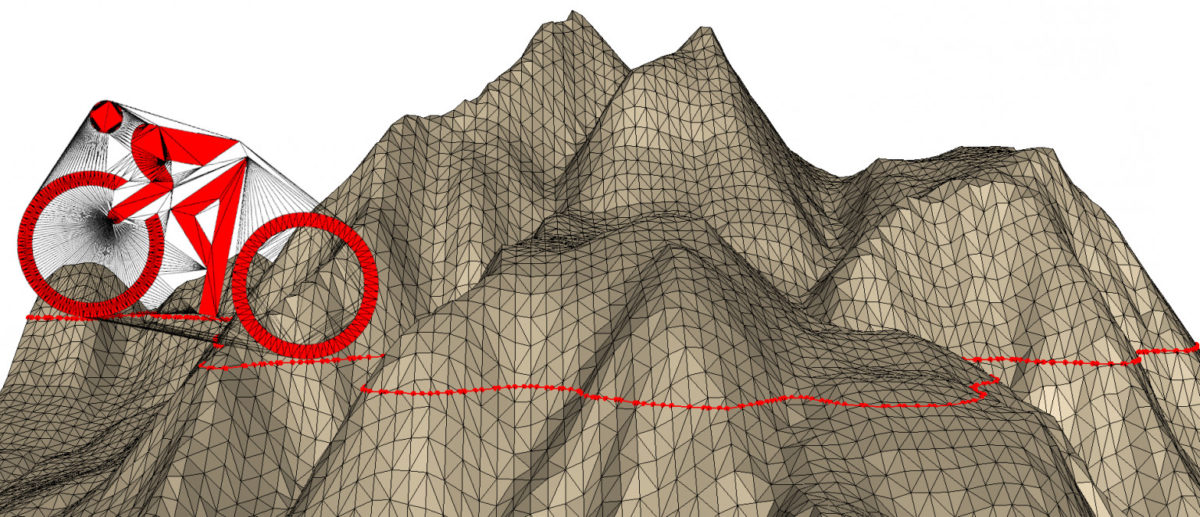
#### 3.1.1 地形建模

Delaunay三角剖分在GIS中广泛用于地形建模，通过将高程数据点连接成三角形网格，可以逼近地形的真实形状。

**算法原理：**

1. 将高程数据点作为Delaunay三角剖分的输入。
2. Delaunay三角剖分算法将数据点连接成三角形网格。
3. 三角形网格的顶点对应于高程数据点，边长表示高程差。

**代码示例：**