Python时间序列聚类分析：从基础到高级应用

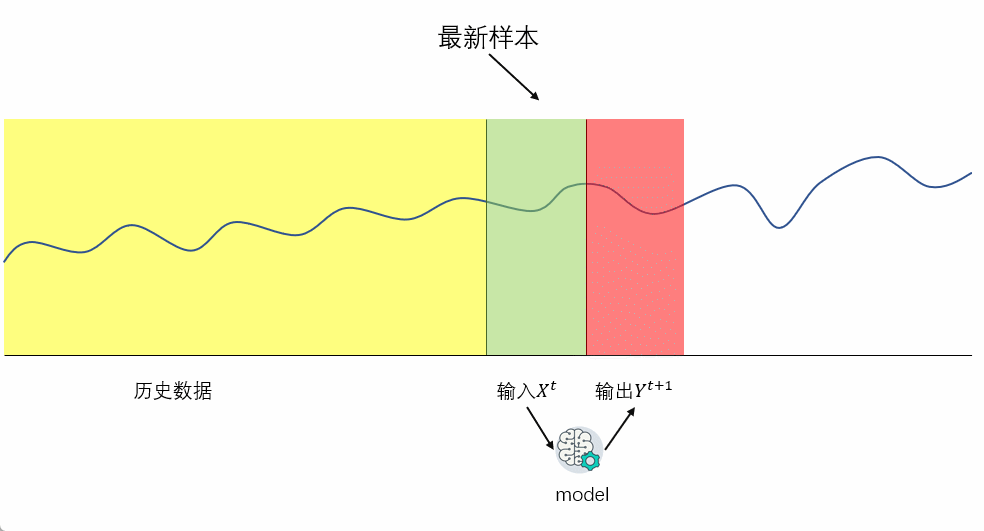
# 1. 时间序列数据与Python基础

在探索时间序列聚类的世界之前，我们必须了解时间序列数据的本质以及Python编程的基础知识。时间序列数据是一种按照时间顺序排列的观测值序列，广泛应用于金融市场分析、天气预报、经济指标监测等领域。掌握时间序列数据的特征和处理方法是进行有效聚类分析的先决条件。

## 1.1 时间序列数据的基本概念

时间序列数据可以看作是一系列按照时间顺序排列的数值点。例如，股票价格、日销售额或者每天的温度记录等，都属于时间序列数据。这些数据点通常是等间隔采集的，但也有不规则间隔的情况。

## 1.2 数据的平稳性与非平稳性

平稳性是时间序列分析中的一个重要概念，指的是时间序列的统计特性不随时间变化。非平稳时间序列的统计特性，如均值、方差等，会随着时间变化。在进行聚类分析之前，确定数据的平稳性状态至关重要，因为非平稳性可能需要通过特定的方法来处理，以确保聚类的有效性。

在Python中，我们可以利用诸如`statsmodels`这样的库来检测时间序列的平稳性，使用`Dickey-Fuller`测试是一种常见的方法。以下是一个简单的代码示例：

import statsmodels.api as sm

# 假设data是一个Pandas Series对象，包含时间序列数据
result = sm.tsa.stattools.adfuller(data)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])

如果p值小于显著性水平（通常为0.05），则可以认为数据是平稳的。反之，如果p值大于显著性水平，则数据非平稳，需要进一步的处理。在后续的章节中，我们将深入探讨如何处理非平稳数据，并进行聚类分析。

# 2. 时间序列聚类分析理论

## 2.1 时间序列数据的特性

### 2.1.1 时序数据的基本概念

时间序列数据是按时间顺序排列的观测数据点集合。在金融、经济、自然科学、社会科学、技术科学等诸多领域中，时间序列分析被广泛应用。它的基本形式是一系列随时间变化的观测值，例如股票价格、销售量、环境温度等。这类数据最显著的特征是它的时间标签，意味着观测值之间存在固有的顺序关系，且通常具有某种依赖性或季节性模式。

在进行时间序列聚类时，识别这些基本特性至关重要，因为它们影响数据的处理方式和最终的聚类效果。例如，季节性或趋势的存在可能会扭曲聚类结果，因此需要事先对其进行调整或建模。

### 2.1.2 数据的平稳性与非平稳性

平稳性是时间序列分析中的一个核心概念。简单来说，平稳的时间序列是指其统计特性（如均值、方差）不随时间变化的序列。对于非平稳时间序列，这些统计特性会随着时间的变化而变化。

- **平稳时间序列**：这类序列的统计特性是恒定的。使用平稳时间序列进行分析时，可以应用许多强大的统计模型，例如自回归移动平均（ARMA）模型。
- **非平稳时间序列**：非平稳性可能表现为趋势、季节性或周期性变化。如果直接对这些序列使用平稳性模型，可能会导致错误的结论。因此，对于非平稳序列，通常需要先进行转换，比如差分、去趋势或季节性调整，以实现平稳化。

## 2.2 聚类分析基础

### 2.2.1 聚类分析的定义与用途

聚类分析是一种无监督学习方法，旨在将数据集中的样本根据某种相似度度量规则划分为多个簇，使得同一个簇内的样本相似度高，而不同簇之间的样本相似度低。它的用途广泛，包括市场细分、社交网络分析、组织大型数据集、图像分割等领域。

聚类不同于分类，因为聚类并不依赖于预先标记的类别信息，而是完全基于数据本身的特征。在时间序列聚类的背景下，这允许我们从无标签的时间序列数据中发现模式和结构。

### 2.2.2 常见聚类算法概述

在时间序列聚类中，有几种算法非常流行：

- **K-均值（K-means）**：这是一种最基础的聚类算法，其核心思想是将数据划分为K个簇，每个簇由一个中心点（质心）代表。K-均值试图最小化簇内的方差。
- **谱聚类（Spectral Clustering）**：该算法使用数据的图表示，并利用拉普拉斯矩阵进行聚类。它在处理非球形簇和发现复杂结构方面表现出色。
- **层次聚类（Hierarchical Clustering）**：这种算法不依赖于预先设定簇的数量。它通过创建一个簇的层次结构（树状图或树）来工作，这种结构可以是凝聚型（自下而上）或分裂型（自上而下）。

## 2.3 时间序列聚类算法的选择与评估

### 2.3.1 算法选择标准

选择适合时间序列聚类的算法时，需考虑以下因素：

- **数据特性**：考虑数据的长度、维度、有无缺失值等因素。例如，对于大型高维时间序列数据集，谱聚类可能更适用。
- **簇的形状与大小**：不同的算法对簇的形状有不同的敏感度。例如，K-均值倾向于找到凸形簇，而谱聚类可以处理更复杂的形状。
- **计算复杂度**：算法的运行时间与空间复杂度需要根据数据规模和处理速度的要求进行考量。

### 2.3.2 评价聚类性能的方法

评价聚类算法性能通常涉及内部指标和外部指标：

- **内部指标**：基于数据集本身的属性，例如轮廓系数（Silhouette Coefficient）和Davies-Bouldin Index，它们无需外部标准即可评估聚类质量。
- **外部指标**：使用已知的标签数据来评价聚类结果，例如调整兰德指数（Adjusted Rand Index）和归一化互信息（Normalized Mutual Information）。

接下来，我们将深入探讨如何通过Python实践时间序列聚类，并对结果进行可视化和分析。

# 3. Python时间序列聚类实践

## 3.1 数据预处理与特征工程

在时间序列分析中，数据预处理和特征工程是至关重要的步骤，