几何布朗运动在计量经济学中的应用：时间序列建模，掌握数据规律

# 1. 几何布朗运动简介

几何布朗运动（GBM）是一种随机过程，用于描述资产价格或其他变量随时间的随机波动。它以其在金融建模中的广泛应用而闻名，特别是股票价格建模。

GBM的数学表达式为：

dS = μSdt + σSdW

其中：

* S 为资产价格
* μ 为漂移率，表示资产价格的长期趋势
* σ 为波动率，表示资产价格的波动程度
* dW 为维纳过程，表示随机噪声

GBM假设资产价格的收益率服从正态分布，并且收益率的方差与时间成正比。这些假设使得GBM在建模资产价格的随机波动方面非常有用。

# 2. 几何布朗运动在时间序列建模中的应用

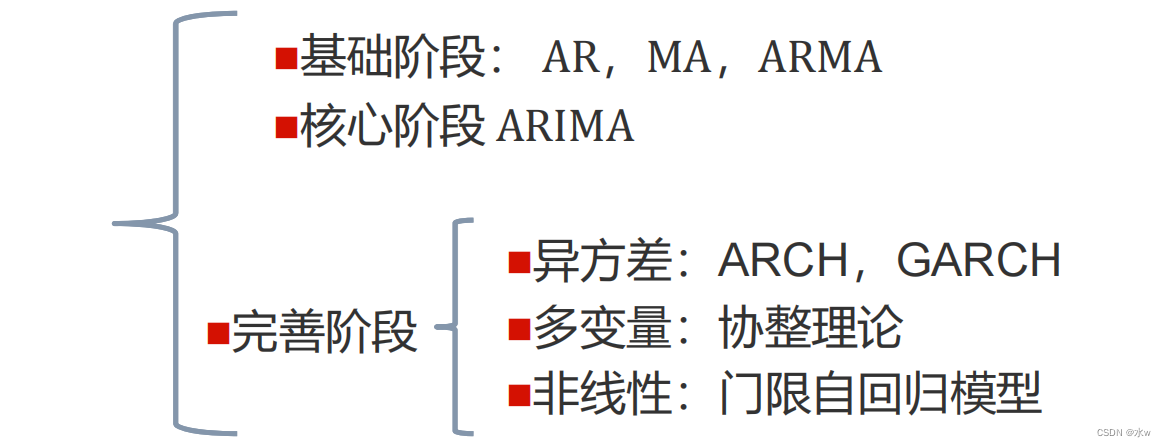
### 2.1 时间序列模型的类型和特点

时间序列模型是一种统计模型，用于对时序数据进行建模和预测。时序数据是指按时间顺序排列的数据，例如股票价格、经济指标或天气数据。时间序列模型可以分为以下几种类型：

- **自回归模型 (AR)**：AR 模型假设时序数据的值仅取决于其过去的值。
- **滑动平均模型 (MA)**：MA 模型假设时序数据的值仅取决于其过去误差项的加权平均值。
- **自回归滑动平均模型 (ARMA)**：ARMA 模型结合了 AR 和 MA 模型，假设时序数据的值取决于其过去的值和误差项。
- **自回归综合滑动平均模型 (ARIMA)**：ARIMA 模型是 ARMA 模型的扩展，增加了差分操作，以处理非平稳时间序列。

### 2.2 几何布朗运动模型的假设和参数估计

几何布朗运动 (GBM) 是一种连续时间随机过程，用于对对数正态分布的时间序列进行建模。GBM 模型的假设如下：

- **对数正态分布**：GBM 模型假设时序数据的对数值服从正态分布。
- **连续时间**：GBM 模型假设时序数据在连续时间内变化。
- **无漂移**：GBM 模型假设时序数据的平均值在时间上保持恒定。
- **常数波动率**：GBM 模型假设时序数据的波动率在时间上保持恒定。

GBM 模型的参数包括：

- **均值回归率 (μ)**：对数正态分布的均值。
- **波动率 (σ)**：对数正态分布的标准差。

这些参数可以通过极大似然估计法进行估计。

### 2.3 几何布朗运动模型的预测和检验

GBM 模型可以用于预测未来时序数据的值。预测过程涉及以下步骤：

1. **估计参数**：使用极大似然估计法估计 GBM 模型的参数。
2. **模拟数据**：使用模拟技术生成 GBM 模型下的未来数据路径。
3. **计算预测**：使用模拟数据计算未来时序数据值的预测值。

GBM 模型的检验可以通过以下方法进行：

- **残差分析**：检查模型残差是否服从正态分布，并且与过去的值不相关。
- **正态性检验**：检验时序数据的对数值是否服从正态分布。
- **波动率检验**：检验时序数据的波动率是否在时间上保持恒定。

**代码块：**

import numpy as np
import pandas as pd
from statsmodels.tsa.statespace.sarimax import SARIMAX

# 加载数据
data = pd.read_csv('time_series_data.csv')

# 拟合 GBM 模型
model = SARIMAX(data, order=(1, 0, 0))
model.fit()

# 预测未来值
forecast = model.forecast(steps=10)

# 绘制预测值
plt.plot(data, label='实际值')
plt.plot(forecast, label='预测值')
plt.legend()
plt.show()

**逻辑分析：**

这段代码使用 Statsmodels 库拟合 GBM 模型并预测未来值。它首先加载数据，然后使用 SARIMAX 类拟合 GBM 模型。接下来，它使用 forecast() 方法预测未来 10 个值。最后，它绘制实际值和预测值。

**参数说明：**

- `data`：要建模的时间序列数据。
- `order`：GBM 模型的阶数，其中 (1, 0, 0) 表示 AR(1) 模型。
- `steps`：要预测的未来步数。

# 3. 几何布朗运动在金融领域的实践

### 3.1 几何布朗运动在股票价格建模中的应用