几何布朗运动与资产配置：优化投资组合，管理风险

# 1. 几何布朗运动的理论基础

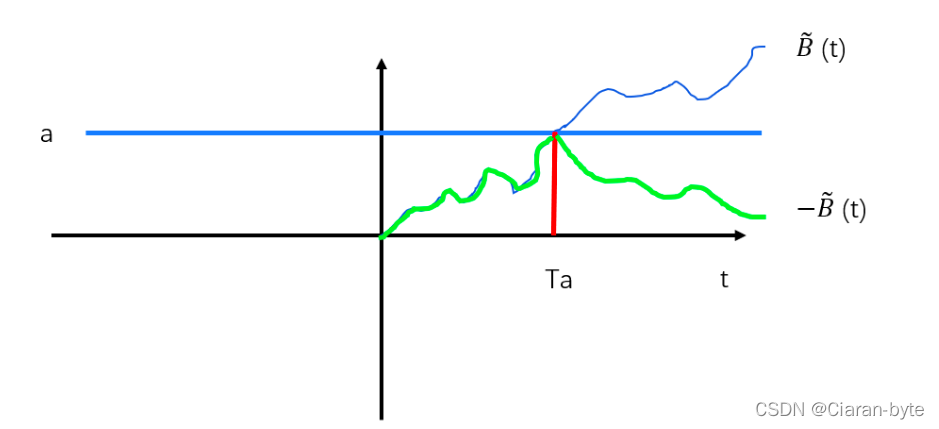
几何布朗运动（GBM）是金融建模中广泛使用的随机过程，它描述了资产价格在给定时间间隔内的随机变化。GBM 的数学公式如下：

dS = μSdt + σSdz

其中：

* `S` 是资产价格
* `μ` 是漂移率，表示资产价格的预期增长率
* `σ` 是波动率，表示资产价格变化的幅度
* `dz` 是标准正态分布的增量

GBM 的主要特点是：

* **连续性：**资产价格的路径是连续的，没有跳跃或间断。
* **正态分布：**资产价格的对数收益服从正态分布。
* **路径依赖性：**资产价格的未来路径取决于其当前值。

# 2 几何布朗运动的实践应用

### 2.1 资产定价模型

几何布朗运动在资产定价模型中发挥着至关重要的作用，为金融资产的定价和风险评估提供了理论基础。

#### 2.1.1 Black-Scholes 模型

Black-Scholes 模型是期权定价最著名的模型之一，它基于几何布朗运动假设，认为标的资产的价格遵循对数正态分布。该模型考虑了期权的执行价格、到期时间、无风险利率和标的资产的波动率等因素，用于计算期权的理论价值。

import numpy as np
from scipy.stats import norm

def black_scholes(S, K, r, sigma, t):
    """
    计算欧式期权的 Black-Scholes 价格。

    参数：
        S: 标的资产的现价
        K: 期权的执行价格
        r: 无风险利率
        sigma: 标的资产的波动率
        t: 期权到期时间（以年为单位）

    返回：
        欧式期权的理论价值
    """

    d1 = (np.log(S / K) + (r + 0.5 * sigma ** 2) * t) / (sigma * np.sqrt(t))
    d2 = d1 - sigma * np.sqrt(t)

    return S * norm.cdf(d1) - K * np.exp(-r * t) * norm.cdf(d2)

逻辑分析：

* `d1`和`d2`是 Black-Scholes 公式中使用的两个中间变量，它们表示期权价值与标的资产价格和执行价格之间的关系。
* `norm.cdf()`函数计算标准正态分布的累积分布函数，它表示在给定`d1`或`d2`值的情况下，正态分布下小于该值的概率。
* `S * norm.cdf(d1)`表示期权的内在价值，即如果期权现在行权，其价值。
* `K * np.exp(-r * t) * norm.cdf(d2)`表示期权的时间价值，即期权到期前可能获得的额外价值。

#### 2.1.2 Merton 模型

Merton 模型是信用风险定价的经典模型，它将几何布朗运动与违约风险相结合。该模型假设公司的资产价值遵循几何布朗运动，违约概率与资产价值成正相关。Merton 模型用于计算信用违约掉期（CDS）和债券的信用利差。

import numpy as np
from scipy.stats import norm

def merton(V, K, r, sigma, rho, PD, R):
    """
    计算 Merton 模型中的信用违约掉期 (CDS) 价格。

    参数：
        V: 公司的资产价值
        K: CDS 的执行价格
        r: 无风险利率
        sigma: 公司资产价值的波动率
        rho: 资产价值和违约概率之间的相关系数
        PD: 公司的违约概率
        R: CDS 的恢复率

    返回：
        CDS 的理论价值
    """

    d1 = (np.log(V / K) + (r - 0.5 * sigma ** 2) * t) / (sigma * np.sqrt(t))
    d2 = d1 - sigma * np.sqrt(t)

    return (V * norm.cdf(d1) - K * np.exp(-r * t) * norm.cdf(d2)) * (1 - PD) + K * PD * R

逻辑分析：

* `d1`和`d2`是 Merton 模型中使用的中间变量，它们与 Black-Scholes 模型中的类似。
* `1 - PD`表示公司不违约的概率。
* `K * PD * R`表示违约时 CDS 支付的金额，其中`R`是恢复率，表示违约后债权人收回的资产价值的百分比。

# 3.1 风险承受能力评估

在制定资产配置策略之前，至关重要的是评估投资者的风险承受能力。这涉及确定投资者愿意承担多少风险以及他们对投资损失的承受能力。风险承受能力评估通常涉及两个关键步骤：

#### 3.1.1 问卷调查

问卷调查是一种广泛使用的方法，用于评估投资者的风险承受能力。问卷通常包括一系列问题，旨在了解投资者的投资目标、时间范围和对风险的看法。这些问题可能包括：

- 您的投资目标是什么？
- 您打算在投资中保持资金多长时间？
- 您对投资损失的承受能力如何？
- 您过去投资的经验是什么？

#### 3.1.2 历史数据分析

除了问卷调查之外，历史数据分析也可以用来评估投资者的风险承受能力。这种方法涉及检查投资者的投资组合历史，以确定他们过去对市场波动和损失的反应。通过分析投资者的投资组合表现，可以得出有关其风险承受能力的宝贵见解。

例如，如果投资者的投资组合在市场下跌期间大幅下跌，则这可能表明他们对风险的承受能力较低。另一方面，如果投资者的投资组合在市场波动期间保持相对稳定，则这可能表明他们对风险的承受能力较高。

**表格：风险承受能力评估问卷示例**

| 问题 | 选项 |
|---|---|
| 您的投资目标是什么？ | 保值、增长、收益 |
| 您打算在投资中保持资金多长时间？ | 短期（<5 年）、中期（5-10 年）、长期（>10 年） |
| 您对投资损失的承受能力如何？ | 非常低、低、中等、高、非常高 |
| 您过去投资的经验是什么？ | 没有经验、有限经验、丰富经验 |

**流程图：风险承受能力评估流程**

graph LR
subgraph 问卷调查
    A[问卷调查] --