【GBM梯度提升机原理大揭秘】：掌握核心机制，提升模型效能

# 1. GBM梯度提升机概述

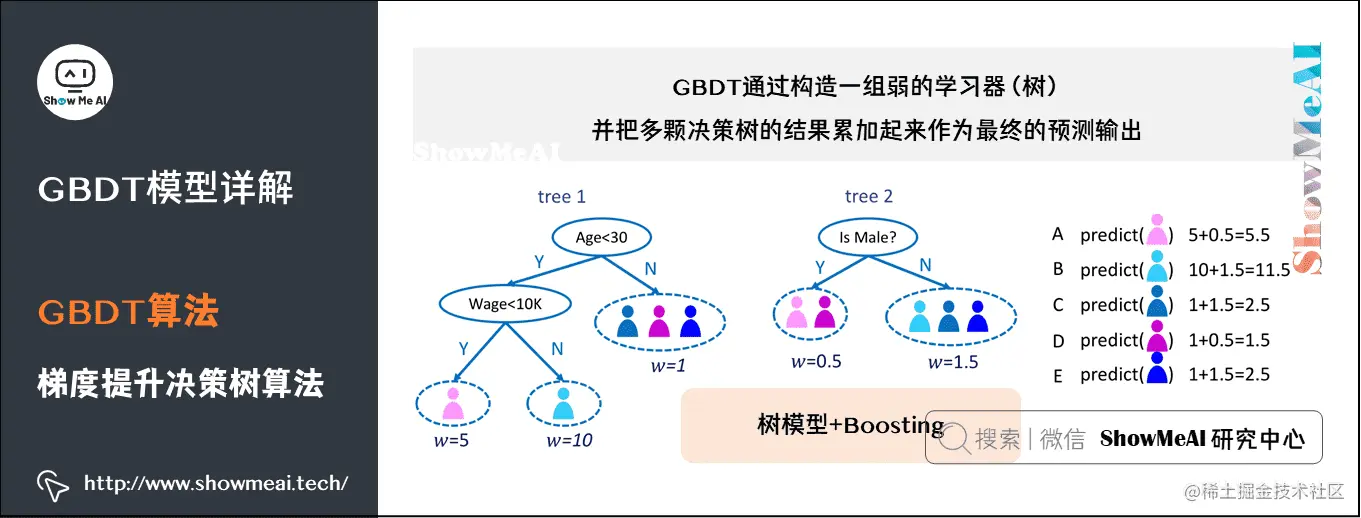
GBM（Gradient Boosting Machine）梯度提升机是一种强大的机器学习算法，广泛应用于分类、回归和排序等任务中。它通过组合多个弱学习器（如决策树）来构建一个强大的模型，从而实现卓越的预测性能。

梯度提升机的核心思想是通过迭代地训练弱学习器来逐步逼近目标函数。在每一轮迭代中，算法计算当前模型的负梯度，并基于此梯度构建一个新的弱学习器。新弱学习器用于更新模型，使模型朝着负梯度方向移动，从而逐步减少损失。

# 2. GBM梯度提升机原理

### 2.1 梯度提升算法的原理

梯度提升算法（Gradient Boosting Algorithm）是一种迭代式机器学习算法，它通过逐次添加决策树模型来提升模型的性能。其核心思想是：在每次迭代中，根据当前模型的预测误差，构造一个新的决策树模型，并将其添加到模型中，以减少整体预测误差。

### 2.2 损失函数与梯度计算

损失函数衡量了模型预测值与真实值之间的差异。梯度提升算法使用损失函数的负梯度作为决策树模型的学习目标。负梯度指示了模型预测误差的方向，从而指导决策树模型的构建。

### 2.3 决策树模型的构建

在每次迭代中，构建一个决策树模型来拟合当前模型的负梯度。决策树通过递归地将数据样本划分为更小的子集，并为每个子集选择一个最优的决策规则，来构建决策边界。

#### 代码块：决策树模型构建

def build_decision_tree(data, target, max_depth=5, min_samples_split=2):
    """
    构建决策树模型

    参数：
        data：训练数据
        target：目标变量
        max_depth：决策树的最大深度
        min_samples_split：划分节点所需的最小样本数

    返回：
        决策树模型
    """

    # 初始化决策树模型
    tree = DecisionTreeClassifier(max_depth=max_depth, min_samples_split=min_samples_split)

    # 训练决策树模型
    tree.fit(data, target)

    return tree

#### 逻辑分析：

该代码块实现了决策树模型的构建。它首先初始化一个决策树模型，指定了最大深度和最小样本数等参数。然后，使用训练数据和目标变量训练决策树模型。训练后，返回训练好的决策树模型。

# 3. GBM梯度提升机算法流程

### 3.1 初始化模型

GBM算法的初始化过程主要包括：

- **设置初始模型：**通常将初始模型设置为一个常数，该常数等于训练数据集的标签值的平均值。
- **计算初始残差：**对于每个训练样本，计算其标签值与初始模型预测值之间的差值，作为初始残差。

### 3.2 迭代训练过程

GBM算法采用迭代训练的方式，在每次迭代中执行以下步骤：

#### 3.2.1 计算负梯度

在第`m`次迭代中，对于每个训练样本，计算其负梯度：

r_mi = -[y_i - f_m(x_i)] * g(y_i, f_m(x_i))

其中：

- `y_i` 是样本`i`的真实标签值
- `f_m(x_i)` 是第`m`次迭代后模型对样本`i`的预测值
- `g(y_i, f_m(x_i))` 是损失函数对预测值`f_m(x_i)`的负梯度

#### 3.2.2 构建决策树

使用负梯度作为训练目标，构建一个新的决策树。该决策树的叶节点数和深度等参数由算法超参数控制。

#### 3.2.3 更新模型

将新构建的决策树添加到模型中，更新模型的预测函数：

f_{m+1}(x) = f_m(x) + h_m(x)

其中：

- `f_m(x)` 是第`m`次迭代后的模型预测函数
- `h_m(x)` 是第`m`次迭代中构建的决策树的预测函数

### 3.2.4 迭代终止条件

GBM算法的迭代过程直到满足以下终止条件之一为止：

- 达到最大迭代次数
- 模型在验证集上的性能不再提升
- 模型收敛，即模型预测值的变化幅度小于某个阈值

# 4. GBM梯度提升机参数调优

### 4.1 决策树参数调优

决策树作为GBM梯度提升机中的基学习器，其参数设置对模型的性能有显著影响。

#### 4.1.1 最大深度

最大深度决定了决策树的复杂度。较大的深度可以拟合更复杂的非线性关系，但容易导致过拟合。较小的深度可以防止过拟合，但可能无法充分捕捉数据的复杂性。

**参数说明：**

max_depth: 整数，表示决策树的最大深度

**代码块：**

# 设置决策树最大深度为 5
max_depth = 5

**逻辑分析：**

设置决策树的最大深度为 5，意味着决策树最多可以有 5 层分支。这有助于防止过拟合，同时仍然允许模型捕捉数据中的非线性关系。

#### 4.1.2 最小样本数

最小样本数决定了决策树在停止分裂之前所需的最小样本数。较小的最小样本数可以生成更复杂的决策树，但容易导致过拟合。较大的最小样本数可以防止过拟合，但可能导致欠拟合。

**参数说明：**

min_samples_split: 整数，表示决策树在分裂节点时所需的最小样本数

**代码块：**

# 设置决策树最小样本数为 10
min_samples_split = 10

**逻辑分析：**

设置决策树最小样本数为 10，意味着决策树在分裂节点时需要至少有 10 个样本。这有助于防止过拟合，同时仍然允许模型捕捉数据中的局部模式。

### 4.2 算法参数调优

除了决策树参数外，GBM梯度提升机算法本身也有一些参数可以调优。

#### 4.2.1 学习率

学习率控制了模型在每次迭代中更新预测值的步长。较大的学习率可以加快模型的收敛速度，但容易导致过拟合。较小的学习率可以防止过拟合，但可能导致模型收敛速度较慢。

**参数说明：**

learning_rate: 浮点数，表示学习率

**代码块：**

# 设置学习率为 0.1
learning_rate = 0.1

**逻辑分析：**

设置学习率为 0.1，意味着模型在每次迭代中更新预测值的步长为 0.1。这有助于平衡模型的收敛速度和过拟合风险。

#### 4.2.2 树的个数

树的个数决定了GBM梯度提升机中使用的决策树的数量。较多的树可以提高模型的准确性，但会增加计算成本。较少的树可以降低计算成本，但可能导致模型欠拟合。

**参数说明：**

n_estimators: 整数，表示决策树的数量

**代码块：**

# 设置决策树数量为 100
n_estimators = 100

**逻辑分析：**

设置决策树数量为 100，意味着模型将使用 100 棵决策树来进行梯度提升。这有助于提高模型的准确性，同时保持合理的计算成本。

# 5. GBM梯度提升机实战应用

### 5.1 数据预处理

GBM梯度提升机对数据质量要求较高，因此在使用前需要对数据进行预处理，主要包括以下步骤：

- **缺失值处理：**缺失值会影响模型的训练和预测，需要对其进行处理。常用的方法有：删除缺失值、填充缺失值（如均值、中位数、众数）或使用插值方法。
- **异常值处理：**异常值会影响模型的稳定性和准确性，需要对其进行处理。常用的方法有：删除异常值、截断异常值（将异常值替换为最大值或最小值）或使用异常值检测算法。
- **数据标准化：**不同的特征可能具有不同的量纲和分布，需要对数据进行标准化，使其具有相似的分布。常用的方法有：均值归一化（将数据减去均值并除以标准差）或最大最小归一化（将数据映射到[0, 1]区间）。
- **特征选择：**GBM梯度提升机可以处理大量特征，但过多的特征会增加训练时间和降低模型的泛化能力。因此，需要对特征进行选择，选择与目标变量相关性较强的特征。常用的特征选择方法有：过滤法（基于特征的统计信息）、包装法（基于模型的性能）和嵌入法（基于模型的训练过程）。

### 5.2 模型训练与评估

数据预处理完成后，即可进行模型训练。GBM梯度提升机训练过程如下：

1. 初始化模型：设置模型参数，如学习率、树的个数和决策树参数。
2. 迭代训练：
- 计算负梯度：计算当前模型对训练数据的负梯度。
- 构建决策树：根据负梯度构建决策树，并确定决策树的分裂点和分裂规则。
- 更新模型：将新构建的决策树添加到模型中，并更新模型的预测值。
3. 停止训练：当满足停止条件（如达到最大迭代次数或训练误差不再下降）时，停止训练。

模型训练完成后，需要对模型进行评估，常用的评估指标有：

- **回归问题：**均方误差（MSE）、平均绝对误差（MAE）、R平方（R2）
- **分类问题：**准确率、召回率、F1值、ROC曲线、AUC

### 5.3 模型调优与部署

GBM梯度提升机的性能受模型参数的影响，因此需要对模型参数进行调优。常用的调优方法有：

- **网格搜索：**在参数的指定范围内，系统地搜索最佳参数组合。
- **随机搜索：**在参数的指定范围内，随机搜索最佳参数组合。
- **贝叶斯优化：**基于贝叶斯定理，迭代更新参数分布，并搜索最佳参数组合。

模型调优完成后，即可将模型部署到生产环境中使用。部署过程包括：

- **模型序列化：**将训练好的模型保存为文件或数据库。
- **模型加载：**在生产环境中加载已保存的模型。
- **模型预测：**使用加载的模型对新数据进行预测。

# 6.1 GBM梯度提升机与其他算法的集成

GBM梯度提升机可以与其他算法集成，以提升模型的性能。常见的集成方法包括：

- **Bagging集成：**将多个GBM模型训练在不同的训练集子集上，然后对它们的预测结果进行平均或投票。Bagging集成可以减少模型的方差，提高泛化能力。
- **Boosting集成：**将多个GBM模型顺序训练，每个模型都使用前一个模型的预测残差作为训练目标。Boosting集成可以减少模型的偏差，提高准确性。
- **Stacking集成：**将多个GBM模型的预测结果作为输入，训练一个新的模型（称为元模型）进行最终预测。Stacking集成可以利用不同模型的优势，提高模型的整体性能。

代码示例：

# Bagging集成
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier

# 创建多个GBM模型
models = [DecisionTreeClassifier() for _ in range(10)]

# 创建Bagging集成模型
bagging_model = BaggingClassifier(models, n_estimators=10)

# 训练Bagging集成模型
bagging_model.fit(X_train, y_train)

# 预测
y_pred = bagging_model.predict(X_test)

## 6.2 GBM梯度提升机在特征工程中的应用

GBM梯度提升机可以用于特征工程，通过以下步骤：

- **特征重要性分析：**GBM模型可以计算每个特征对模型预测结果的影响，从而确定特征的重要性。
- **特征选择：**根据特征重要性，选择具有高重要性的特征，剔除不重要的特征。
- **特征变换：**使用GBM模型的决策树结构，对原始特征进行变换，生成新的特征。

代码示例：

# 特征重要性分析
importances = model.feature_importances_

# 特征选择
selected_features = [i for i, importance in enumerate(importances) if importance > 0.05]

# 特征变换
new_features = model.apply(X_train)[['feature1', 'feature2']]

## 6.3 GBM梯度提升机在深度学习中的应用

GBM梯度提升机可以与深度学习模型集成，以提升模型的性能。常见的集成方法包括：

- **GBM预训练：**使用GBM模型对原始数据进行预训练，然后将预训练的特征作为深度学习模型的输入。
- **GBM特征选择：**使用GBM模型选择重要的特征，然后将这些特征作为深度学习模型的输入。
- **GBM集成：**将GBM模型与深度学习模型集成，形成一个混合模型。

代码示例：

# GBM预训练
gbm_model = GradientBoostingClassifier()
gbm_model.fit(X_train, y_train)

# 预训练特征
pre_features = gbm_model.apply(X_train)[['feature1', 'feature2']]

# 深度学习模型
dnn_model = tf.keras.models.Sequential()
dnn_model.add(tf.keras.layers.Dense(128, activation='relu', input_dim=2))
dnn_model.add(tf.keras.layers.Dense(1, activation='sigmoid'))

# 训练深度学习模型
dnn_model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
dnn_model.fit(pre_features, y_train, epochs=10)