【进阶】主成分分析(PCA)在图像数据降维中的应用

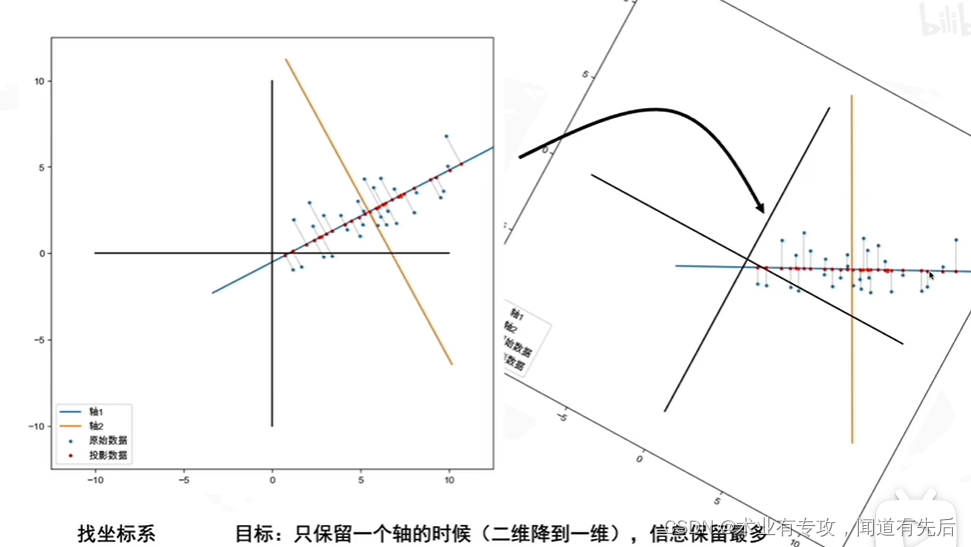
# 1. 主成分分析（PCA）理论基础**

主成分分析（PCA）是一种广泛用于数据降维的统计技术。它通过将原始数据投影到一个新的正交基上，来识别数据中的主要特征。PCA 的核心思想是最大化投影数据的方差，从而保留原始数据中最重要的信息。

在数学上，PCA 可以表示为：

X = UΣV^T

其中：

* X 是原始数据矩阵
* U 是特征向量矩阵
* Σ 是特征值矩阵
* V^T 是特征向量矩阵的转置

# 2. PCA在图像数据降维中的应用实践

### 2.1 图像数据的预处理

#### 2.1.1 图像归一化和标准化

图像归一化和标准化是图像数据预处理中常用的技术，它们可以将图像像素值映射到一个特定的范围，从而提高PCA降维的效率和效果。

**归一化**将图像像素值缩放到[0, 1]或[-1, 1]的范围内，公式如下：

normalized_image = (image - image.min()) / (image.max() - image.min())

**标准化**将图像像素值减去均值并除以标准差，公式如下：

standardized_image = (image - image.mean()) / image.std()

#### 2.1.2 图像降噪和去噪

图像降噪和去噪可以去除图像中的噪声，提高PCA降维的准确性。常用的降噪方法包括：

**均值滤波**：用图像中相邻像素的平均值替换当前像素值。

**中值滤波**：用图像中相邻像素的中值替换当前像素值。

**高斯滤波**：用一个高斯核与图像卷积，实现平滑效果。

### 2.2 PCA降维算法的实现

#### 2.2.1 PCA算法原理和数学推导

PCA算法通过寻找数据协方差矩阵的特征向量和特征值，将数据投影到一个新的正交坐标系中，从而实现降维。

设原始数据矩阵为X，协方差矩阵为C，则特征值分解公式为：

C = VΛV^T

其中，V为特征向量矩阵，Λ为特征值对角矩阵。

#### 2.2.2 PCA算法的Python实现

import numpy as np
from sklearn.decomposition import PCA

# 加载图像数据
image_data = ...

# 归一化图像数据
image_data = (image_data - image_data.min()) / (image_data.max() - image_data.min())

# 创建PCA对象
pca = PCA(n_components=0.95)

# 拟合PCA模型
pca.fit(image_data)

# 获取降维后的数据
reduced_image_data = pca.transform(image_data)

### 2.3 降维效果的评估

#### 2.3.1 降维前后图像质量的对比

降维前后图像质量的对比可以通过以下指标评估：

**峰值信噪比（PSNR）**：衡量降维后图像与原始图像之间的失真程度。

**结构相似性指数（SSIM）**：衡量降维后图像与原始图像之间的结构相似性。

#### 2.3.2 降维后图像特征的分析

降维后图像特征的分析可以评估PCA降维是否保留了图像的重要特征。常用的分析方法包括：

**主成分分析**：分析PCA提取的主成分的分布和权重。

**可视化**：将降维后的图像与原始图像进行可视化对比，观察降维对图像特征的影响。

# 3. PCA降维在图像处理中的应用案例

### 3.1 图像压缩

#### 3.1.1 PCA降维压缩原理

PCA降维压缩是一种通过降维技术减少图像数据量的方法。其基本原理是将图像数