【进阶】透视变换与应用实例

# 2.1 齐次坐标系与透视变换矩阵

### 2.1.1 齐次坐标系的定义和性质

齐次坐标系是一种将点、线和面的几何关系表示为向量的方法。它通过在笛卡尔坐标系中增加一个额外的维度来实现，称为齐次坐标。齐次坐标系中的点由一个四元组表示：

[x, y, z, w]

其中：

* `x`、`y` 和 `z` 是笛卡尔坐标系中的坐标
* `w` 是齐次坐标

齐次坐标系的性质包括：

* **齐次性：**对于任何非零标量 `k`，`[x, y, z, w]` 和 `[kx, ky, kz, kw]` 表示相同的点。
* **仿射不变性：**齐次坐标系下的仿射变换（平移、旋转、缩放）保持齐次坐标不变。
* **透视投影：**当 `w` 为 0 时，齐次坐标系中的点表示无穷远点。

# 2. 透视变换的实现方法

### 2.1 齐次坐标系与透视变换矩阵

#### 2.1.1 齐次坐标系的定义和性质

齐次坐标系是一种扩展的坐标系，它在笛卡尔坐标系的基础上增加了额外的维度，通常称为齐次维度。齐次坐标系中的点由一个四元组表示，其中前三个分量表示笛卡尔坐标，第四个分量称为齐次坐标。

齐次坐标系具有以下性质：

- 齐次坐标系的点可以表示为一个向量或矩阵。
- 齐次坐标系的点可以通过一个非奇异矩阵进行变换。
- 齐次坐标系的点可以通过齐次变换进行变换，齐次变换保持点之间的相对位置关系。

#### 2.1.2 透视变换矩阵的推导

透视变换是一种将三维点投影到二维平面的变换。透视变换矩阵是一个 3x4 矩阵，它可以将三维点投影到齐次二维坐标系中。

透视变换矩阵的推导如下：

import numpy as np

# 定义三维点
p = np.array([x, y, z, 1])

# 定义投影矩阵
P = np.array([[f, 0, cx, 0],
              [0, f, cy, 0],
              [0, 0, 1, 0]])

# 进行透视变换
p_prime = np.dot(P, p)

其中：

- `f` 是焦距。
- `cx` 和 `cy` 是主点坐标。
- `p` 是三维点。
- `p_prime` 是投影后的齐次二维坐标。

### 2.2 透视变换的算法和优化

#### 2.2.1 透视变换的算法原理

透视变换的算法原理如下：

1. 将三维点投影到齐次二维坐标系中。
2. 对齐次二维坐标进行仿射变换。
3. 将齐次二维坐标投影回三维坐标系。

#### 2.2.2 透视变换的优化方法

透视变换的优化方法主要有：

- **最小二乘法：**通过最小化投影误差来优化透视变换矩阵。
- **RANSAC：**通过随机采样和一致性检验来优化透视变换矩阵。
- **Levenberg-Marquardt 算法：**通过迭代的方式优化透视变换矩阵。

# 3.1 图像矫正和校正

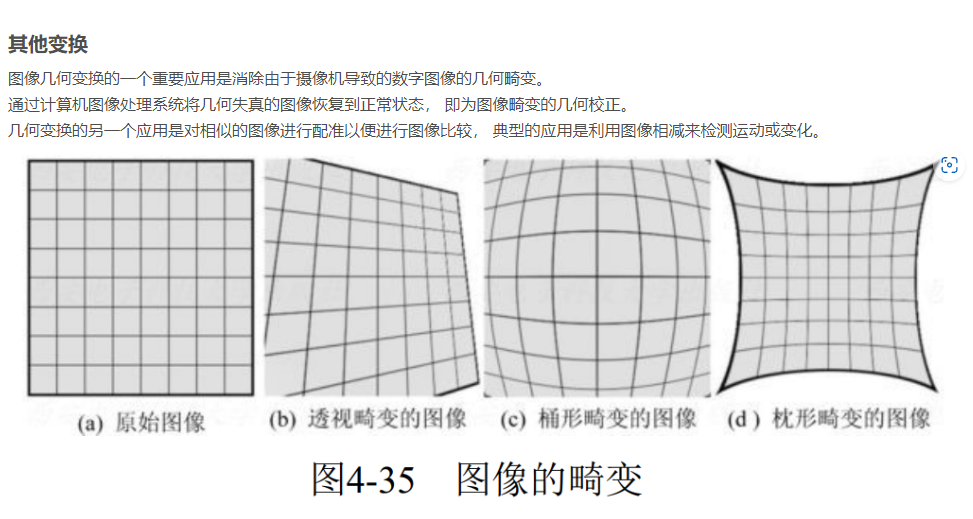
#### 3.1.1 图像畸变的类型和成因

图像畸变是指图像中物体形状或尺寸与实际情况不符的现象。图像畸变通常是由镜头畸变、透视畸变或其他因素造成的。

* **镜头畸变**是由镜头的设计和制造缺陷造成的，它会使图像中的直线出现弯曲或变形。
* **透视畸变**是由相机与拍摄对象之间的相对位置造成的，它会使图像中的物体看起来比实际情况更大或更小。

#### 3.1.2 透视变换在图像矫正中的应用

透视变换可以用来矫正图像中的透