【特征选择与模型性能】：数据集优化的8个实战策略

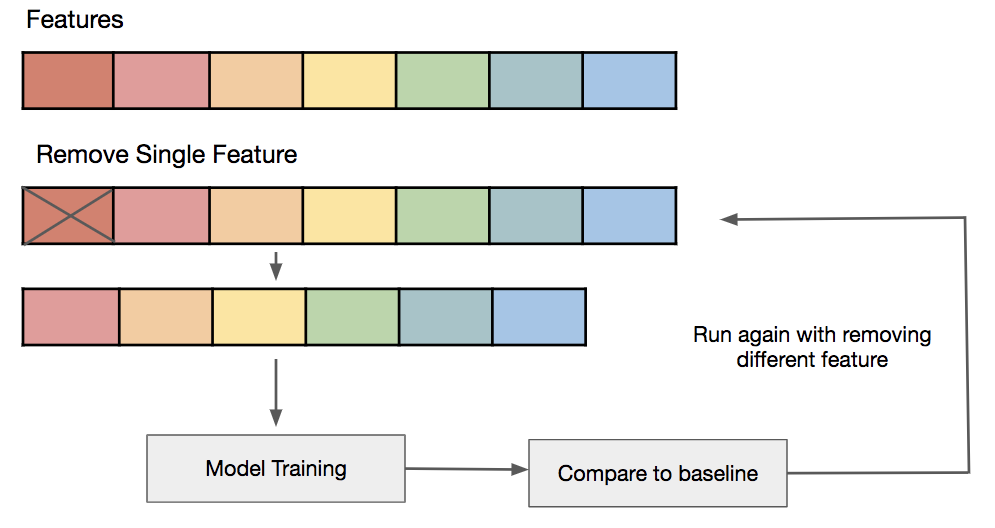
# 1. 特征选择与模型性能概述

## 章节概述

在构建和训练机器学习模型时，特征选择扮演着至关重要的角色。它不仅影响模型的准确性，还涉及到模型训练的时间和效率。通过选择合适的特征子集，我们可以减少模型复杂性，避免过拟合，并可能提高模型的泛化能力。本章将简要介绍特征选择的基本概念以及它与模型性能之间的关系，为后续章节的深入探讨打下基础。

## 特征选择的目的和意义

特征选择的首要目的是提升模型的性能。通过识别并保留与模型输出密切相关的特征，我们可以减少不必要的噪声，简化模型结构，从而加速训练过程并提高预测准确率。此外，特征选择还有助于提高模型的可解释性，使模型更易于理解与维护。

## 特征选择对模型性能的影响

特征选择对模型性能的影响体现在多个方面。首先，它能够减少模型训练的数据维度，从而减少计算成本。其次，合适的特征选择有助于去除无关特征，降低过拟合风险。最后，减少特征数量还可以改善模型的泛化能力，使其在新的、未见过的数据上表现更优。

# 2. 理论基础与特征重要性评估

## 2.1 特征选择的理论基础

### 2.1.1 特征选择的目的和意义

特征选择是机器学习领域的一个基本步骤，其核心目的在于从原始数据集中挑选出最有代表性的特征子集，从而提高模型的训练效率和预测性能。在处理实际问题时，数据往往包含大量冗余或无关的信息，这不仅会降低学习算法的效率，还可能对模型的泛化能力产生负面影响。特征选择作为一种降维技术，可以有效地减少模型训练所需的计算资源，增强模型对新数据的泛化能力，以及提高模型的可解释性。

### 2.1.2 特征选择的分类与方法概述

特征选择方法大致可以分为三大类：过滤法（Filter），封装法（Wrapper），和嵌入法（Embedded）。过滤法通过统计测试独立于学习算法，通常速度快、计算复杂度低，但可能不会考虑特征之间的依赖性。封装法将特征选择作为一个搜索问题，利用学习算法的性能来指导特征的选择，它能够较好地评估特征子集的性能，但通常计算代价较高。嵌入法在模型训练的过程中结合特征选择，它通过引入正则化项或构建基于决策树的复杂模型来实现特征选择，这种方法既考虑了特征的重要性，也考虑了特征之间的相互作用，是一种有效而直接的方法。

## 2.2 特征重要性评估

### 2.2.1 相关性分析方法

相关性分析是一种常用的过滤法特征选择方法，主要包括相关系数、卡方检验和互信息等。这些方法依据统计量对特征与目标变量之间的相关性进行评价。例如，皮尔逊相关系数能够衡量连续变量间的线性关系；卡方检验可以用来判断分类变量与目标类别之间的独立性；互信息能够衡量任意类型变量间的统计依赖性。通过设置阈值，相关性分析方法可以识别出与目标变量强相关的特征，剔除那些不相关的特征。

import numpy as np
import pandas as pd
from scipy.stats import pearsonr

# 示例：使用皮尔逊相关系数进行特征选择
def pearson_correlation(df, target_column):
    corr_matrix = df.corr()
    target_corr = corr_matrix[target_column].abs().sort_values(ascending=False)
    return target_corr

# 假定df是我们的数据集，且包含目标列
dataframe = pd.DataFrame(np.random.rand(100, 10), columns=list('ABCDEFGHIJ'))
target_corr = pearson_correlation(dataframe, 'J')

print(target_corr)

上代码中，我们首先导入必要的库，并定义了一个函数来计算目标列与数据集中其他特征列的皮尔逊相关系数。函数返回一个降序排列的相关系数序列，方便我们识别出与目标列最相关的特征。

### 2.2.2 基于模型的特征重要性评估

基于模型的特征重要性评估方法通常涉及使用特定的算法来训练模型，并评估各特征对模型性能的影响。一些树模型，如随机森林和梯度提升决策树，提供了一种内置的特征重要性评估机制。这些模型能够为每个特征提供一个评分，这个评分代表了该特征对模型预测能力的贡献度。通常，这些评分可用于过滤掉重要性较低的特征。

from sklearn.ensemble import RandomForestClassifier

# 使用随机森林分类器进行特征重要性评估
def feature_importances_with_random_forest(df, target_column):
    X = df.drop(target_column, axis=1)
    y = df[target_column]
    forest = RandomForestClassifier()
    forest.fit(X, y)
    importances = forest.feature_importances_
    indices = np.argsort(importances)[::-1]
    print("Feature ranking:")
    for f in range(X.shape[1]):
        print("%d. feature %d (%f)" % (f + 1, indices[f], importances[indices[f]]))

feature_importances_with_random_forest(dataframe, 'J')

在上述代码段中，我们使用了scikit-learn库中的`RandomForestClassifier`来训练一个随机森林模型。模型训练完成后，通过访问`feature_importances_`属性，我们可以获取一个特征重要性评分列表，并打印出排名前几的特征。

### 2.2.3 信息论方法在特征选择中的应用

信息论提供了一种量化描述变量之间相互关系的手段。互信息（Mutual Information, MI）是衡量两个变量之间共享信息量的指标。在特征选择中，可以使用互信息来评估特征和目标变量之间的相互依赖性。互信息的最大化有助于选取那些能够提供最多目标变量信息的特征。使用互信息方法时，通常会选择与目标变量互信息值最高的特征作为重要特征。

from sklearn.feature_selection import mutual_info_classif

# 使用互信息方法进行特征选择
def mutual_information_feature_selection(df, target_column):
    X = df.drop(target_column, axis=1)
    y = df[target_column]
    mi_scores = mutual_info_classif(X, y)
    mi_df = pd.DataFrame(mi_scores, index=X.columns, columns=['MI Scores'])
    mi_df = mi_df.sort_values('MI Scores', ascending=False)
    print(mi_df)

mutual_information_feature_selection(dataframe, 'J')

在上述代码段中，我们利用`mutual_info_classif`函数计算了数据集中每个特征与目标列之间的互信息值。这个函数返回了一个评分数组，我们将其转换为DataFrame格式，并按照互信息值降序排列，以识别出最重要的特征。

通过对特征选择理论基础的探讨和特征重要性评估的实践方法的分析，下一章我们将深入探讨特征选择的算法实践，包括过滤法、封装法和嵌入法的具体应用。

# 3. 特征选择的算法实践

在机器学习领域，特征选择是模型建立过程中的一个关键步骤。正确选择特征不仅能减少模型的复杂度，还能提高模型的预测性能。本章深入探讨特征选择中常用的三种算法：过滤法、封装法和嵌入法。我们将分析它们的原理、适用场景和优缺点。

## 3.1 过滤法特征选择

过滤法是一种简单的特征选择方法，它通过统计测试对每个特征进行评分，选择分数最高的特征。这种方法计算效率高，通常用于初步筛选特征。

### 3.1.1 单变量统计测试

单变量统计测试是过滤法中的一种常见技术。它使用诸如卡方检验、ANOVA、互信息等方法独立地评估每个特征与目标变量之间的关系。

**代码块 3.1.1 - 卡方检验示例**

from scipy.stats import chi2_contingency

# 假设 contingency_table 是一个观察频数表
chi2, p, dof, expected = chi2_contingency(contingency_table)

# p值小于阈值（例如 0.05）表示特征与目标变量有关联
print("卡方值:", chi2)
print("p值:", p)

在上面的代码中，`chi2_contingency` 函数计算卡方统计量，用于判断两个分类变量是否独立。p值小于某个阈值（如0.05）时，表示两个变量之间存在关联，该特征可能是有用的。

### 3.1.2 相关系数和卡方检验

相关系数用于度量特征与目标变量之间的线性关系强度，例如皮尔逊相关系数。卡方检验则适用于分类变量，评估特征和目标变量的独立性。

**表格 3.1.1 - 相关系数和卡方检验对比**

| 检验类型 | 适用数据类型 | 特点 |
|----------|--------------|------|
| 相关系数 | 连续变量 | 能捕捉线性关系，但忽略非线性关系 |
| 卡方检验 | 分类变量 | 评估独立性，但不度量关系强度 |

相关系数和卡方检验的对比，展示了两种方法不同的适用范围和局限性。在实际应用中，选择合适的方法对于提升特征选择的有效性至关重要。

## 3.2 封装法特征选择

封装法特征选择涉及使用机器学习模型作为特征选择的黑箱。通过训练模型并评估特征的性能，此方法可以找到最佳特征组合。

### 3.2.1 嵌入式方法的实践应用

嵌入式方法，如基于模型的特征选择，通常会在模型训练过程中集成特征选择步骤。

**代码块 3.2.1 - 使用Ridge回归进行特征选择**

from sklearn.linear_model import Ridge

# 假设 X 是特征矩阵，y 是目标变量
ridge = Ridge(alpha=1.0)
ridge.fit(X, y)

# 使用系数来评估特征重要性
feature_importance = np.abs(ridge.coef_)

上述代码展示了如何使用Ridge回归进行特征选择。Ridge回归模型会通过正则化项来惩罚大系数，从而实现特征选择的效果。特征重要性是通过模型系数的绝对值来确定的。

### 3.2.2 基于模型的封装方法实例

基于模型的封装方法的一个典型例子是使用决策树模型来进行特征选择。

**mermaid流程图 3.2.2 - 决策树模型特征选择流程**

graph TD
    A[开始] --> B[加载数据集]
    B --> C[建立决策树模型]
    C --> D[评估特征重要性]
    D --> E[选择重要特征]
    E --> F[结束]

流程图描绘了使用决策树进行特征选择的过程。通过评估每个特征在决策树中的重要性，我们可以选出有助于预测目标变量的特征。

## 3.3 嵌入法特征选择

嵌入法特征选择结合了过滤法和封装法的特点，通过在算法中直接进行特征选择来提升效率和效果。

### 3.3.1 基于LASSO和Ridge回归的特征选择

LASSO和Ridge回归是常见的线性模型，能够通过正则化来进行特征选择。

**代码块 3.3.1 - 使用LASSO进行特征选择**

from sklearn.linear_model import LassoCV

# 假设 X 是特征矩阵，y 是目标变量
lasso = LassoCV()
lasso.fit(X, y)

# 打印LASSO回归选择的特征
print("选择的特征索引:", lasso.support_)

LASSO回归通过引入L1范数作为正则项，能够在训练过程中将一些特征的系数压缩到零，从而实现特征选择。上述代码段展示了如何使用LASSO回归选择特征。

### 3.3.2 基于决策树和森林的特征选择

随机森林可以用来估计特征的重要性，它通过考虑多个决策树对特征的分割频率来实现。

**表格 3.3.1 - 嵌入法特征选择方法对比**

| 方法 | 原理 | 优势 | 劣势 |
|------|------|------|------|
| LASSO | L1正则化导致稀疏解 | 自动特征选择 | 对于高度共线性的特征效果不佳 |
| 随机森林 | 基于树的集成学习 | 可以处理非线性关系 | 可能会高估某些特征的重要性 |

嵌入法中LASSO和随机森林对比，显示了各自的优势和可能的劣势。在实际应用中，应根据数据集的具体特点和模型需求来选择合适的方法。

通过本章节对过滤法、封装法和嵌入法的详细介绍和实例演示，我们可以看到每种方法都有其适用场景和限制。理解这些方法对于机器学习实践者来说是至关重要的，能够帮助他们选择最适合其问题的特征选择策略。在下一章节中，我们将探讨特征选择在模型训练中的应用，进一步深入理解特征选择的实践价值。

# 4. 特征选择在模型训练中的应用

特征选择是机器学习模型训练过程中一个关键步骤，它通过剔除不相关或者冗余的特征来提高模型的性能和可解释性。在本章中，我们将探讨特征选择如何在分类、回归以及聚类问题中得到应用，并展示具体的实践案例和代码演示。

## 4.1 特征选择在分类问题中的应用

分类问题是机器学习中常见的任务之一，如判断邮件是否为垃圾邮件，或者识别图像中的物体等。特征选择能够帮助分类模型降低维度，简化模型结构，并提升分类性能。

### 4.1.1 特征选择在支持向量机中的应用

支持向量机（SVM）是一种有效的分类器，但它对于高维数据的表现很敏感。通过特征选择减少维度，可以有效防止过拟合并提高模型的泛化能力。

#### 实践案例

假设我们使用SVM对鸢尾花数据集进行分类。数据集包含150个样本，每个样本有4个特征。为了减少维度，我们使用递归特征消除（RFE）方法来选择最重要的特征。

from sklearn.svm import SVC
from sklearn.feature_selection import RFECV
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# 加载数据集
iris = load_iris()
X, y = iris.data, iris.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 使用RFE方法选择特征
svc = SVC(kernel="linear")
selector = RFECV(estimator=svc, step=1, cv=5)
selector = selector.fit(X_train, y_train)

# 输出特征选择的结果
print("Optimal number of features: %d" % selector.n_features_)
print("Selected features: %s" % str(selector.support_))

# 使用选定的特征训练SVM模型
svc.fit(X_train[:, selector.support_], y_train)

通过上述代码，我们可以看到RFE方法帮助我们从原始的4个特征中选择了最合适的数量，并使用这些特征训练了一个更简洁的SVM模型。

### 4.1.2 特征选择在神经网络中的应用

神经网络通常需要大量的数据和计算资源来训练，同时过度的特征也可能导致模型复杂和过拟合。在某些情况下，减少特征的数量不仅能够节省资源，还可能提高模型的泛化能力。

#### 实践案例

下面是一个使用特征选择优化神经网络模型的例子。我们将使用同样的鸢尾花数据集，通过主成分分析（PCA）来选择特征，并将结果与未进行特征选择的网络进行比较。

from sklearn.decomposition import PCA
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import Adam

# 数据预处理
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
pca = PCA(n_components=2)
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)

# 构建神经网络模型
model = Sequential()
model.add(Dense(12, input_dim=2, activation='relu'))
model.add(Dense(8, activation='relu'))
model.add(Dense(3, activation='softmax'))

# 编译模型
***pile(loss='categorical_crossentropy', optimizer=Adam(), metrics=['accuracy'])

# 训练模型
model.fit(X_train, keras.utils.to_categorical(y_train), epochs=150, batch_size=10, verbose=0)

# 评估模型
scores = model.evaluate(X_test, keras.utils.to_categorical(y_test), verbose=0)
print("\n%s: %.2f%%" % (model.metrics_names[1], scores[1]*100))

在这个案例中，我们使用PCA将数据集降至两个主成分，这样可以减少神经网络的输入特征数量。通过实验，我们可以分析特征数量减少对模型性能的影响。

## 4.2 特征选择在回归问题中的应用

回归任务旨在预测连续值输出。特征选择在回归模型中的应用同样重要，它有助于避免复杂模型在测试集上表现不佳的情况。

### 4.2.1 特征选择在线性回归中的应用

线性回归模型对特征的数量较为敏感，特别是当特征之间存在多重共线性时。特征选择可以帮助我们找到一组最佳特征，以提高线性回归模型的预测精度。

#### 实践案例

我们将使用波士顿房价数据集来展示特征选择在线性回归中的应用。首先，我们将利用逐步回归法（Stepwise Regression）来选择特征，并对比选择前后的模型性能。

import numpy as np
import pandas as pd
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, StepwiseRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 加载数据集
boston = load_boston()
X, y = boston.data, boston.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 使用逐步回归选择特征
model = StepwiseRegression()
model.fit(X_train, y_train)

# 输出选择的特征
selected_features = boston.feature_names[model.get_support()]
print("Selected features:", selected_features)

# 训练线性回归模型
reg = LinearRegression()
reg.fit(X_train[:, model.get_support()], y_train)

# 预测并计算均方误差
y_pred = reg.predict(X_test[:, model.get_support()])
mse = mean_squared_error(y_test, y_pred)
print("Mean Squared Error: %.2f" % mse)

### 4.2.2 特征选择在多元回归模型中的应用

多元回归模型可能包含大量的输入特征，其中一些特征可能对预测目标变量的实际影响不大。通过使用特征选择技术，我们可以剔除不相关的特征，提升模型的可解释性和预测效果。

#### 实践案例

下面展示一个使用信息增益（Information Gain）方法在多元回归模型中进行特征选择的案例。我们还是使用波士顿房价数据集，并将信息增益作为选择标准。

from sklearn.feature_selection import SelectKBest, f_regression

# 使用信息增益选择特征
selector = SelectKBest(f_regression, k='all')
X_train_selected = selector.fit_transform(X_train, y_train)

# 获取每个特征的信息增益分数
scores = selector.scores_
feature_names = boston.feature_names
info_gain_dict = dict(zip(feature_names, scores))

# 输出信息增益分数并选择最佳特征
print("Feature scores based on Information Gain:")
for feature, score in sorted(info_gain_dict.items(), key=lambda item: item[1], reverse=True):
    print("%s: %f" % (feature, score))

# 使用选定特征训练线性回归模型并评估性能
reg = LinearRegression()
reg.fit(X_train_selected[:, :5], y_train)  # 假设我们选择前5个最佳特征
y_pred = reg.predict(X_test[:, :5])
mse = mean_squared_error(y_test, y_pred)
print("Mean Squared Error with selected features: %.2f" % mse)

在这个案例中，我们使用了`SelectKBest`方法和`f_regression`评分函数来选择与目标变量相关的特征，并仅使用这些特征训练回归模型。

## 4.3 特征选择在聚类问题中的应用

聚类是一种无监督学习方法，用于将数据集中的样本划分为不同的类别。特征选择在聚类中的作用是减少特征的数量，从而简化计算过程和提高聚类的可解释性。

### 4.3.1 特征选择在K-means聚类中的应用

K-means是一种常见的聚类算法，它对特征的数量和特征间的关系比较敏感。使用特征选择可以提高聚类的效率和质量。

#### 实践案例

我们将使用K-means聚类算法在鸢尾花数据集上进行聚类。为了选择有助于聚类的特征，我们先使用主成分分析（PCA）来降低维度。

from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

# 数据预处理
iris = load_iris()
X = iris.data
y = iris.target
pca = PCA(n_components=2)
X_reduced = pca.fit_transform(X)

# 使用K-means聚类
kmeans = KMeans(n_clusters=3, random_state=42)
clusters = kmeans.fit_predict(X_reduced)

# 绘制聚类结果
plt.scatter(X_reduced[clusters == 0, 0], X_reduced[clusters == 0, 1], label="Cluster 1")
plt.scatter(X_reduced[clusters == 1, 0], X_reduced[clusters == 1, 1], label="Cluster 2")
plt.scatter(X_reduced[clusters == 2, 0], X_reduced[clusters == 2, 1], label="Cluster 3")
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=300, c='red', label="Centroids")
plt.title("K-means clustering on Iris dataset")
plt.legend()
plt.show()

### 4.3.2 特征选择在层次聚类中的应用

层次聚类是一种基于距离的聚类方法，它构建了一个特征之间的关系层次。在处理高维数据时，特征选择可以减少计算量，并提高聚类的质量。

#### 实践案例

下面我们将使用鸢尾花数据集，通过特征选择后进行层次聚类。我们将使用相关矩阵和特征重要性评分来选择特征，并展示聚类结果。

from sklearn.cluster.hierarchical import AgglomerativeClustering
import scipy.cluster.hierarchy as shc

# 数据预处理
X = iris.data
y = iris.target

# 使用相关矩阵作为距离矩阵
corr_matrix = np.corrcoef(X.T)
plt.figure(figsize=(10, 8))
dendrogram = shc.dendrogram(shc.linkage(corr_matrix, method='complete'), labels=iris.target_names)
plt.title('Hierarchical Clustering Dendrogram')
plt.xlabel('Features')
plt.ylabel('Distance')
plt.show()

# 使用特征选择后的数据进行层次聚类
selected_features = ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)']  # 假设我们选择了这三个特征
X_selected = X[:, [iris.feature_names.index(feature) for feature in selected_features]]
hierarchical_cluster = AgglomerativeClustering(n_clusters=3)
clusters = hierarchical_cluster.fit_predict(X_selected)

# 绘制聚类结果
plt.figure(figsize=(10, 8))
plt.scatter(X_selected[:, 0], X_selected[:, 1], c=clusters, cmap='viridis')
plt.title('Hierarchical Clustering')
plt.xlabel(selected_features[0])
plt.ylabel(selected_features[1])
plt.show()

在这个案例中，我们使用了相关矩阵作为距离矩阵来构建层次聚类的树状图，并选择了重要的特征进行层次聚类。通过图形可以清晰地看到不同层次的聚类结构。

在本章中，我们详细探讨了特征选择在模型训练中的应用，并通过实践案例演示了如何在分类、回归和聚类问题中应用特征选择技术。特征选择不仅简化了模型，还能够提升模型性能和可解释性。在后续的章节中，我们将进一步讨论特征选择的优化策略与挑战，以及如何在实际机器学习项目中整合特征选择。

# 5. 特征选择的优化策略与挑战

特征选择是一个重要的数据预处理步骤，在提高模型性能的同时，减少了模型训练的时间和资源消耗。随着机器学习领域的深入发展，特征选择面临一些优化策略和挑战，本章将探讨高维数据下的特征选择、优化方法以及特征选择中的挑战和未来方向。

## 5.1 高维数据的特征选择

在机器学习和数据分析中，高维数据是指拥有大量特征的数据集。高维数据会带来计算复杂度高、内存消耗大、过拟合风险增加等问题。在本小节中，我们将探讨这些问题，并提供相应的特征选择策略。

### 5.1.1 高维数据的挑战

高维数据的一个主要挑战是所谓的“维度的诅咒”（Curse of Dimensionality），这表示当特征数量增加时，数据的稀疏性也会增加。这意味着需要更多的数据来保持统计估计的准确性，否则模型会更容易过拟合。此外，高维空间的计算复杂度也更高，可能需要指数级的时间来执行一些算法。

### 5.1.2 高维数据的特征选择策略

为了应对高维数据的挑战，我们可以采用一些高效的特征选择策略。首先，可以通过降低特征空间的维度来解决维度的诅咒问题。具体方法包括：

- **主成分分析（PCA）**：这是一种降维技术，它可以提取数据中的关键信息并转换成新的特征集合，这些新特征称为主成分。
- **线性判别分析（LDA）**：LDA是一种监督学习的降维技术，旨在寻找一个变换，使得数据投影到新的特征空间后能够得到更好的类别区分。

除了这些基于变换的方法外，我们还可以使用基于模型的特征选择方法，如LASSO或Ridge回归，它们通过引入L1或L2正则化项来自然地进行特征选择。

## 5.2 特征选择优化方法

优化特征选择不仅能提升模型的预测能力，还能加快模型训练的速度。在本小节中，我们将探讨一些常用的特征选择优化方法。

### 5.2.1 正则化方法的优化应用

正则化方法如L1和L2正则化在特征选择中有着广泛的应用，尤其是在线性模型中。L1正则化（LASSO）能够产生稀疏的权重向量，从而实现特征选择，因为其能够在优化过程中将某些特征的权重降至零。

import numpy as np
from sklearn.linear_model import LassoCV

# 示例数据集
X = np.random.rand(100, 10)  # 100个样本，10个特征
y = np.random.rand(100)  # 目标值

# 使用LASSO回归进行特征选择
lasso = LassoCV(cv=5).fit(X, y)

print("Selected features (non-zero coefficients):")
print(np.nonzero(lasso.coef_)[0])

上面的代码展示了如何使用LASSO回归进行特征选择。`LassoCV`类会在交叉验证的过程中自动选择合适的正则化强度，并且通过`coef_`属性显示每个特征的系数，其中系数为零的特征即为被选择掉的特征。

### 5.2.2 组合优化和遗传算法的应用

组合优化方法如遗传算法（Genetic Algorithms, GA）在特征选择中也有着优异的表现。遗传算法是一种模拟自然选择过程的优化算法，它通过交叉、变异和选择操作来迭代地改进候选解。

在特征选择问题中，我们可以将每种特征组合视为一个潜在的解决方案，然后通过遗传算法来迭代地寻找最佳特征组合。这种方法可以处理大量的特征，并且避免了穷举搜索的计算负担。

## 5.3 特征选择面临的挑战和未来方向

尽管特征选择是一个已研究多年的问题，但它仍存在许多挑战和值得探索的新方向。

### 5.3.1 特征选择中的过拟合问题

特征选择的一个主要挑战是过拟合。当数据集有限时，保留过多的特征可能会导致模型学习到数据中的噪声，而不是潜在的信号。为了减少过拟合的风险，我们需要采用能够平衡模型复杂度与数据拟合度的特征选择方法。

### 5.3.2 特征选择研究的新趋势

随着深度学习的发展，特征学习（representation learning）已经成为特征选择研究的新趋势。特征学习是通过学习数据的表示来自动化特征选择的过程，它通常依赖于深度神经网络来提取复杂数据的有效特征。

此外，新的特征选择算法不断被提出，例如基于互信息的特征选择、基于模型集成的特征选择等。这些新方法旨在解决特定问题或提高特征选择的效率和准确性。

通过本章节的介绍，我们详细探讨了特征选择的优化策略与挑战，包括高维数据的特征选择策略、优化方法以及未来的研究趋势。在下一章中，我们将通过案例研究和实战演练，进一步巩固和深化对特征选择的理解。

# 6. 案例研究与实战演练

在机器学习项目的实施过程中，特征选择不是一个孤立的环节，而是与数据预处理、模型构建、参数优化和性能评估等多个环节紧密相连。本章将通过一个真实的案例研究，展示特征选择在机器学习项目中的整合过程，并对实战演练中的关键步骤进行详细说明。

## 6.1 真实数据集的特征选择实战

### 6.1.1 数据预处理和探索性数据分析

在开始特征选择之前，首先需要进行数据预处理和探索性数据分析（EDA），这是确保后续模型效果的基础。数据预处理包括缺失值处理、异常值检测、数据标准化或归一化以及数据类型转换等。例如，在Python中，可以使用Pandas和Scikit-learn库进行数据预处理：

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# 假设 df 是一个已经加载的Pandas DataFrame
# 处理缺失值
df.fillna(df.mean(), inplace=True)

# 检测并处理异常值（这里是一个简化的示例）
for col in df.select_dtypes(include=[np.number]).columns:
    df = df[(np.abs(stats.zscore(df[col])) < 3)]

# 数据标准化
scaler = StandardScaler()
df_scaled = scaler.fit_transform(df.select_dtypes(include=[np.number]))

# 将处理后的数据转换回DataFrame
df_scaled = pd.DataFrame(df_scaled, columns=df.select_dtypes(include=[np.number]).columns)

# 探索性数据分析
df_scaled.describe()

### 6.1.2 不同方法的特征选择比较分析

在数据预处理完成后，接下来进行特征选择。这一阶段可以尝试不同的特征选择方法，比较它们的效果。以下是一些常用方法的Python代码示例：

from sklearn.feature_selection import SelectKBest, f_classif

# 假设 X 是特征集，y 是目标变量
# 使用单变量统计测试选择K个最佳特征
select_k_best = SelectKBest(f_classif, k=5)
X_k_best = select_k_best.fit_transform(X, y)

# 查看被选中的特征
selected_features = select_k_best.get_support(indices=True)
df.iloc[:, selected_features].head()

此外，还可以使用基于模型的方法，如使用随机森林的特征重要性进行特征选择，或利用递归特征消除（RFE）等。

## 6.2 特征选择在机器学习项目中的整合

### 6.2.1 特征选择与模型调优的集成

特征选择完成后，下一步是将选定的特征与机器学习模型集成。在这一阶段，可以使用交叉验证和网格搜索等技术来调优模型参数。在Python中，使用Scikit-learn的`GridSearchCV`可以很容易地完成这一任务：

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV

# 使用随机森林分类器
rf_clf = RandomForestClassifier()

# 设定要调优的参数网格
param_grid = {
    'n_estimators': [100, 200],
    'max_depth': [10, 20, 30],
    'min_samples_split': [2, 5]
}

# 使用GridSearchCV进行模型调优
grid_search = GridSearchCV(rf_clf, param_grid, cv=5)
grid_search.fit(X_k_best, y)

# 查看最佳参数和得分
best_params = grid_search.best_params_
best_score = grid_search.best_score_

### 6.2.2 模型性能评估与特征选择效果验证

最后，通过一系列的性能指标来评估模型的预测效果，如准确率、精确率、召回率、F1分数等。同时，可以使用特征选择前后模型性能的对比来验证特征选择的效果。在Python中，使用Scikit-learn的分类报告和混淆矩阵可以进行这些性能评估：

from sklearn.metrics import classification_report, confusion_matrix

# 使用最佳模型参数和选定的特征训练模型
best_clf = grid_search.best_estimator_
y_pred = best_clf.predict(X_k_best)

# 输出性能报告
report = classification_report(y, y_pred)
print(report)

# 绘制混淆矩阵
conf_matrix = confusion_matrix(y, y_pred)
import seaborn as sns
sns.heatmap(conf_matrix, annot=True, fmt="d")

通过上述步骤，特征选择不再是一个单独的环节，而是与模型构建和评估紧密集成，共同推动机器学习项目的成功实施。在实战演练中，数据科学家将能够更深入地理解特征选择的重要性和实际应用。