【机器学习数据预处理全解】：12个案例揭示提升模型性能的秘密

# 1. 数据预处理基础概念

## 数据预处理的重要性

在数据分析和机器学习的项目中，原始数据往往需要经过一系列的预处理步骤才能被用于模型训练。数据预处理是确保数据质量的关键环节，它涉及对数据进行清理、转换、规范化等操作，以消除噪声和不一致性，提高数据质量，最终促进模型的表现和准确性。基础概念部分将介绍数据预处理的目标和意义，为后续更深入的技术讨论打下基础。

## 数据预处理的目标

数据预处理的主要目标包括但不限于：

1. 提高数据质量：通过清洗数据，移除无关特征和异常值，确保数据的准确性和可靠性。
2. 优化模型性能：通过适当的预处理方法，如数据标准化和归一化，减少模型训练的计算复杂性，并提升模型的收敛速度。
3. 提升特征表达能力：通过特征构造、特征选择等技术，增强模型对数据内在结构的理解，从而提高模型的预测能力。

## 数据预处理的类型

数据预处理通常可以分为以下几类：

- 数据清洗：移除或处理异常值和缺失值，识别并修正数据中的错误或不一致。
- 数据转换：将数据转换为适合分析的形式，如特征编码、提取、构造新特征等。
- 数据降维：通过技术和算法减少数据集的维度，去除冗余和相关性高的特征，降低模型复杂性。
- 数据集划分：合理划分数据集，为模型的训练和测试提供独立的数据子集。
- 数据标准化和归一化：调整数据分布，使不同特征具有可比性，提高算法性能。

以上为第一章内容，接下来的章节将深入探讨每一种预处理技术的细节和应用场景。

# 2. 数据清洗技巧

在数据科学和机器学习项目中，数据清洗是一个至关重要的步骤，它直接影响到模型的训练效果和最终的预测性能。数据清洗的过程涉及识别和处理缺失值、异常值以及标准化和归一化数据，以便为后续的分析和建模做好准备。

## 2.1 缺失值处理

### 2.1.1 缺失值识别方法

缺失值是数据集中常见的问题，可能由多种原因造成，如数据收集不完整、传输错误等。识别缺失值是处理它们的第一步。最常用的方法包括：

- **统计方法**：通过统计函数如`pandas`库中的`isnull()`和`notnull()`来检查缺失值。
- **可视化方法**：利用箱形图、热图等可视化技术来直观展示数据中的缺失情况。

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# 加载数据集
df = pd.read_csv('dataset.csv')

# 识别缺失值
missing_values = df.isnull().sum()
print(missing_values)

# 可视化缺失值
sns.heatmap(df.isnull(), cbar=False)
plt.show()

在上述代码中，我们首先使用`pandas`库加载了一个数据集，并使用`isnull()`方法检查了每个特征的缺失情况。然后，我们使用`seaborn`和`matplotlib`库来生成一个热图，可视化地展示了数据集中的缺失值情况。

### 2.1.2 缺失值填补策略

一旦识别出缺失值，接下来需要决定如何处理这些缺失值。常见的填补策略包括：

- **删除**：如果缺失值不多，可以考虑直接删除含缺失值的行或列。
- **填充**：可以用均值、中位数、众数或预设值等来填充缺失值。

# 删除含有缺失值的行
df_clean = df.dropna()

# 填充缺失值
df_filled = df.fillna(df.mean())

上述代码展示了两种处理缺失值的策略：`dropna()`方法用于删除含有缺失值的行，而`fillna()`方法则用各特征的均值填充缺失值。

## 2.2 异常值处理

### 2.2.1 异常值的识别技术

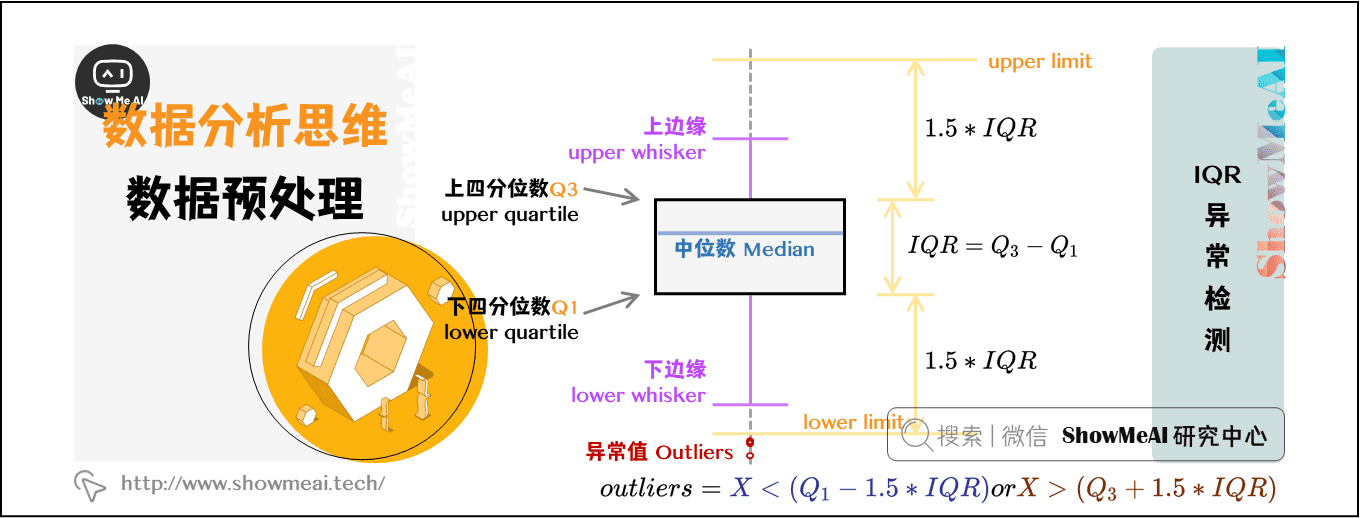
异常值是数据集中明显偏离其他观测值的点。识别异常值的技术包括：

- **统计测试**：例如Z-score、IQR（四分位距）。
- **可视化方法**：如箱形图、散点图等。

# 使用IQR识别异常值
Q1 = df.quantile(0.25)
Q3 = df.quantile(0.75)
IQR = Q3 - Q1

lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR

# 标记异常值
outliers = df[~((df >= lower_bound) & (df <= upper_bound)).all(axis=1)]
print(outliers)

在这段代码中，我们首先计算了数据集的四分位数，然后根据IQR识别了异常值，并将其打印出来。

### 2.2.2 异常值的处理方法

处理异常值的常用方法包括：

- **删除**：对于确信是错误的异常值，可以直接删除。
- **变换**：对数据进行变换，如对数变换，以减少异常值的影响。

# 删除异常值
df_no_outliers = df[~((df >= lower_bound) & (df <= upper_bound)).all(axis=1)]

# 对数变换减少异常值影响
df_transformed = np.log(df + 1)

在这段代码中，我们首先删除了异常值，然后使用了对数变换来处理剩余的数据。

## 2.3 数据标准化和归一化

### 2.3.1 标准化与归一化的意义

标准化和归一化是数据预处理中重要的步骤，它们能够确保数据在相同的尺度下，从而提高算法的收敛速度和性能。

- **标准化**：通过减去均值并除以标准差，使数据的均值为0，标准差为1。
- **归一化**：通常指的是将数据缩放到[0,1]区间内。

### 2.3.2 实现标准化和归一化的技术

Python中`scikit-learn`库提供了方便的标准化和归一化工具：

from sklearn.preprocessing import StandardScaler, MinMaxScaler

# 标准化
scaler = StandardScaler()
df_scaled = scaler.fit_transform(df)

# 归一化
min_max_scaler = MinMaxScaler()
df_normalized = min_max_scaler.fit_transform(df)

在这段代码中，我们使用`StandardScaler`类对数据集进行了标准化处理，而`MinMaxScaler`类则用于归一化数据。

以上章节展示了处理缺失值、异常值以及数据标准化和归一化的技术和策略，是数据预处理过程中的基础步骤。通过合理的数据清洗，可以显著提升数据质量，为后续的数据分析和模型训练打下坚实的基础。

# 3. 数据转换技术

## 3.1 特征编码

### 3.1.1 类别特征编码方法

类别特征是数据集中常见的非数值类型数据，这类数据通常无法直接用于大多数机器学习模型中，因此需要转换为数值形式。类别特征编码方法是将类别变量转换为适合机器学习算法处理的数值型变量的过程。

#### 一对一编码(One-hot Encoding)

一对一编码是将每一个类别值都转换为一个新的二进制（0/1）列。这种方法适用于类别间没有顺序关系的情况，如颜色、性别等。

import pandas as pd
from sklearn.preprocessing import OneHotEncoder

# 示例数据
data = {'Color': ['Red', 'Blue', 'Green']}
df = pd.DataFrame(data)

# 进行One-hot编码
encoder = OneHotEncoder(sparse=False)
encoded_array = encoder.fit_transform(df[['Color']])
encoded_df = pd.DataFrame(encoded_array, columns=encoder.get_feature_names_out(['Color']))

print(encoded_df)

#### 标签编码(Label Encoding)

标签编码是将每一个类别值都转换为一个整数，适用于类别间具有自然顺序的情况。

from sklearn.preprocessing import LabelEncoder

# 示例数据
data = {'Size': ['Small', 'Medium', 'Large']}
df = pd.DataFrame(data)

# 进行标签编码
label_encoder = LabelEncoder()
df['Size'] = label_encoder.fit_transform(df['Size'])

print(df)

### 3.1.2 非数值特征编码方法

非数值特征，例如日期时间、文本等，通常需要更复杂的转换方法以保留其数据结构和语义信息。

#### 时间戳编码

时间戳编码将日期时间转换为可计算的数值，常见的是提取时间戳中的年、月、日、小时等信息。

from datetime import datetime
import pandas as pd

# 示例数据
data = {'Timestamp': [datetime(2023, 1, 1), datetime(2023, 1, 2)]}
df = pd.DataFrame(data)

# 提取时间特征
df['Year'] = df['Timestamp'].dt.year
df['Month'] = df['Timestamp'].dt.month
df['Day'] = df['Timestamp'].dt.day
df['Hour'] = df['Timestamp'].dt.hour

print(df)

#### 文本特征编码

文本数据经常通过词袋模型（Bag of Words）或TF-IDF（Term Frequency-Inverse Document Frequency）模型进行数值转换。

from sklearn.feature_extraction.text import TfidfVectorizer

# 示例文本数据
text_data = ['This is a sample document', 'This document is very useful']
corpus = text_data

# 创建TF-IDF转换器
tfidf_vectorizer = TfidfVectorizer()
tfidf_matrix = tfidf_vectorizer.fit_transform(corpus)

print(tfidf_matrix.toarray())

## 3.2 特征提取与构造

### 3.2.1 主成分分析(PCA)

主成分分析（PCA）是一种常用的降维技术，其目的是通过线性变换将原始数据转换为一组各维度线性无关的表示，同时保留最重要的数据特性。

#### PCA的数学原理

PCA的核心是通过正交变换将可能相关的变量转换为一组线性不相关的变量，这些变量称为主成分。第一主成分具有最大的方差，第二主成分与第一主成分正交，并具有次大的方差，依此类推。

import numpy as np
from sklearn.decomposition import PCA

# 假设X是我们的数据矩阵
X = np.array([[1, 2], [3, 4], [5, 6]])

# 创建PCA实例，指定要保留的主成分数量为1
pca = PCA(n_components=1)

# 应用PCA
X_pca = pca.fit_transform(X)

print(X_pca)

### 3.2.2 特征选择方法

特征选择是从原始特征集中选择出有助于提高预测模型性能的一组特征的过程。

#### 过滤方法(Filter Methods)

过滤方法通过统计测试来评价和选择特征，不依赖于任何机器学习算法，如卡方检验、相关系数等。

from sklearn.feature_selection import SelectKBest, f_classif

# 假设X是我们的特征数据，y是目标变量
X = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
y = np.array([0, 1, 0])

# 使用ANOVA F-value选择最好的2个特征
selector = SelectKBest(f_classif, k=2)
X_new = selector.fit_transform(X, y)

print(X_new)

## 3.3 多项式特征与交互项

### 3.3.1 多项式特征的生成

多项式特征扩展是指创建原始特征的高阶组合，如平方、交叉项等。这样可以增加模型的非线性表达能力。

#### 多项式特征的生成

from sklearn.preprocessing import PolynomialFeatures

# 示例数据
X = np.arange(4).reshape(2, 2)
poly = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly.fit_transform(X)

print(X_poly)

### 3.3.2 交互项的利用与意义

交互项是指两个或多个变量的组合，它可以捕捉变量间的交互效应。

#### 利用交互项

import pandas as pd

# 假设有一个数据集
data = {'Feature1': [1, 2, 3], 'Feature2': [4, 5, 6]}
df = pd.DataFrame(data)

# 交互项的生成
df['Interaction'] = df['Feature1'] * df['Feature2']

print(df)

交互项的意义在于，它们可以提供额外的信息，帮助模型更好地理解不同特征如何共同作用影响目标变量。在机器学习中，添加交互项通常可以提升模型的预测性能。

# 4. 数据降维方法

## 4.1 主成分分析(PCA)
### 4.1.1 PCA的理论基础
主成分分析（Principal Component Analysis，PCA）是一种常用的数据降维技术，其目标是通过正交变换将一组可能相关的变量转换为一组线性不相关的变量，这些新的变量称为主成分。PCA 的核心思想是将高维数据投影到低维空间，同时尽可能保留数据中的关键信息。

PCA 的数学原理基于数据的协方差矩阵，通过特征值分解来找到数据的主要变化方向。在数学上，PCA 寻找数据方差最大的方向，并将数据投影到这些方向上，这些方向就是数据的主要成分。第一主成分对应于最大的特征值，第二主成分对应于次大的特征值，以此类推。通常情况下，前几个主成分就足以代表原始数据集中的大部分信息。

### 4.1.2 PCA的实现和案例应用
在 Python 中，PCA 可以通过 `sklearn.decomposition` 模块中的 PCA 类来实现。以下是一个简单的例子，展示如何使用 PCA 对数据集进行降维处理。

import numpy as np
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler

# 假设 X 是一个形状为 (n_samples, n_features) 的数据集
# 为了使结果稳定，通常先对数据进行标准化处理
scaler = StandardScaler()
X_std = scaler.fit_transform(X)

# 初始化 PCA 对象，设定要保留的主成分数量，例如保留95%的数据方差
pca = PCA(n_components=0.95)
X_pca = pca.fit_transform(X_std)

# X_pca 现在包含了降维后的数据

在这个例子中，我们首先导入了必要的模块，并假设有一个数据集 `X`。我们首先使用 `StandardScaler` 对数据进行了标准化处理，这是因为 PCA 是基于协方差矩阵的，而协方差矩阵对于数据的缩放很敏感。接着，我们初始化了一个 PCA 对象，并指定了希望保留的主成分的方差比例（这里为95%）。最后，使用 `fit_transform` 方法对数据进行了降维。

## 4.2 线性判别分析(LDA)
### 4.2.1 LDA的数学原理
线性判别分析（Linear Discriminant Analysis，LDA）是一种用于分类问题的降维技术。LDA 的目标是找到一个线性组合的特征空间，使得在这个空间中，不同类别的数据尽可能地分开。

LDA 假设不同类别的数据服从高斯分布，并且各个类别的协方差相同。LDA 的算法可以分为两步：首先，根据类内散度矩阵和类间散度矩阵计算最佳投影方向；然后，将数据投影到这个方向上。类间散度矩阵描述了不同类别数据之间的差异，而类内散度矩阵描述了同一个类别内数据的分布情况。LDA 旨在最大化类间散度矩阵与类内散度矩阵的比值，从而达到分类的目的。

### 4.2.2 LDA在分类问题中的应用
LDA 在解决分类问题时非常有用，尤其是当数据集的维度很高且每个类别的样本数量相对较少时。与 PCA 相比，LDA 不仅降维，还考虑了类别的信息，因此在很多情况下能够提供更好的分类效果。

在 Python 中使用 LDA 可以通过 `sklearn.discriminant_analysis` 模块中的 LinearDiscriminantAnalysis 类来实现。以下是一个简单的例子：

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA

# 假设 X 是特征数据，y 是标签数据
# 初始化 LDA 对象，设定降维后的维度数量
lda = LDA(n_components=2)
X_lda = lda.fit_transform(X, y)

# X_lda 现在包含了降维后的数据，可以用于后续的分类任务

在这个例子中，我们使用 LDA 对原始数据集 `X` 进行降维处理，并且指定了降维后的维度数量为2。这是因为二维数据很容易进行可视化，帮助我们理解数据在降维后的分布情况。

## 4.3 t分布随机邻域嵌入(t-SNE)
### 4.3.1 t-SNE的算法思想
t分布随机邻域嵌入（t-distributed Stochastic Neighbor Embedding，t-SNE）是一种非线性降维方法，特别适用于高维数据的可视化。t-SNE 将高维数据点映射到二维或三维空间中，使得相似的数据点在低维空间中也彼此接近，而不相似的数据点则远离。

t-SNE 的算法基于概率分布，首先在高维空间定义了一个条件概率分布，表示为高维空间中任意两个点作为邻域的概率。接着，在低维空间定义了一个类似的条件概率分布。t-SNE 通过最小化高维和低维空间的概率分布之间的 Kullback-Leibler 散度来寻找低维空间中的点，这样就实现了将数据集中的相似点在低维空间中聚集在一起。

### 4.3.2 t-SNE的案例展示和注意事项
由于 t-SNE 是一种非线性降维方法，并且具有参数可调、随机初始化等特点，它特别适合于数据的可视化分析。在使用 t-SNE 时，有几个参数需要特别注意：

- `perplexity`：这个参数类似于邻域的大小，影响着 t-SNE 的局部和全局特性。一般而言，数据量较大时选择较高的 perplexity 值。
- `learning_rate`：控制着迭代过程中的步长，若数据点过于分散或过于聚集时，可能需要调整该参数。
- `n_iter`：表示迭代次数，t-SNE 是通过迭代优化过程，因此合理的迭代次数可以达到更好的可视化效果。

下面是一个使用 t-SNE 的 Python 代码示例：

from sklearn.manifold import TSNE

# 假设 X 是已经预处理好的高维数据集
# 初始化 t-SNE 对象，这里设定降维后的维度为2，用于可视化
tsne = TSNE(n_components=2, perplexity=30, n_iter=1000)
X_tsne = tsne.fit_transform(X)

# X_tsne 现在包含了降维后的数据，可以用于绘图和后续分析

在这个例子中，我们使用 t-SNE 对原始数据集 `X` 进行降维处理，设置降维后的维度为2，并指定了 perplexity 参数值为30。这样处理后的数据 `X_tsne` 可以直接用于绘图，观察数据在二维空间中的分布情况。由于 t-SNE 的随机性，建议多次运行代码以获得稳定的结果。

# 5. 数据集划分与交叉验证

数据科学和机器学习中，模型的构建只是第一步，更重要的是如何评价模型的泛化能力，即在未知数据上的表现。在这一章节中，我们将深入探讨如何合理划分训练集、验证集和测试集以及使用交叉验证技术来提高模型评估的准确性。

## 5.1 训练集、验证集和测试集的划分

### 5.1.1 合理划分数据集的重要性

在机器学习任务中，为了评估模型对未知数据的泛化能力，需要将数据分为训练集、验证集和测试集。训练集用于模型学习，验证集用于模型选择和参数调整，测试集用于最终评估模型性能。合理划分数据集可以避免过拟合和欠拟合，提高模型的泛化能力。划分的不恰当可能会导致模型在未见过的数据上表现不佳。

### 5.1.2 数据集划分的方法与技巧

#### 比例划分法

最常见的是比例划分法，即将数据集按照一定比例划分为训练集、验证集和测试集。例如，可以使用80%的数据作为训练集，10%作为验证集，10%作为测试集。这可以通过简单的随机抽样实现。

#### 分层抽样法

在数据类别分布不均衡的情况下，应使用分层抽样法以保证各类别在各个数据集中的比例与整体数据集一致。这种方法有助于避免在某些类别上训练不足或过度拟合。

from sklearn.model_selection import train_test_split

# 假设X是特征数据，y是目标变量
X_train, X_temp, y_train, y_temp = train_test_split(X, y, test_size=0.2, stratify=y, random_state=42)
X_val, X_test, y_val, y_test = train_test_split(X_temp, y_temp, test_size=0.5, stratify=y_temp, random_state=42)

#### 时间序列数据划分

对于时间序列数据，不能简单地使用随机抽样，而应该按照时间顺序划分数据集，以避免数据泄露和未来信息的不当使用。

def time_series_split(data, n_test):
    X, y = data[:, :-1], data[:, -1]
    X_train, X_test, y_train, y_test = [], [], [], []
    for i in range(n_test, len(X)):
        X_train.append(X[i-n_test:i])
        y_train.append(y[i-n_test:i])
        X_test.append(X[i])
        y_test.append(y[i])
    return np.array(X_train), np.array(X_test), np.array(y_train), np.array(y_test)

## 5.2 交叉验证技术

### 5.2.1 K折交叉验证的原理

K折交叉验证是将数据集划分为K个大小相同的子集，轮流将每个子集作为验证集，其余的K-1个子集作为训练集。通过K次训练和验证，得到一个更为稳定和全面的模型性能评估。K折交叉验证能够有效利用有限的数据，提高评估的可靠性。

### 5.2.2 不同交叉验证方法的应用场景

#### 常规K折交叉验证

适用于大多数机器学习任务，尤其是数据集大小适中时。

from sklearn.model_selection import cross_val_score

# 假设X和y已经准备好，estimator是模型实例
k = 5
scores = cross_val_score(estimator, X, y, cv=k)
print(f'K折交叉验证得分: {scores.mean()}')

#### 留一交叉验证

特别适用于小规模数据集。留一交叉验证是K折交叉验证的一个特例，其中K等于样本数，每次只留一个样本作为验证集。

from sklearn.model_selection import LeaveOneOut

loo = LeaveOneOut()
scores = cross_val_score(estimator, X, y, cv=loo)
print(f'留一交叉验证得分: {scores.mean()}')

#### 分层K折交叉验证

与常规K折交叉验证类似，但适用于类别不平衡的数据集。它确保每个折中每个类别都有代表，以获得更公平和准确的模型性能估计。

from sklearn.model_selection import StratifiedKFold

skf = StratifiedKFold(n_splits=k)
scores = cross_val_score(estimator, X, y, cv=skf)
print(f'分层K折交叉验证得分: {scores.mean()}')

总结来说，数据集划分与交叉验证是机器学习模型构建中至关重要的步骤。通过合理的划分和交叉验证策略，可以确保模型能够准确地在未知数据上进行泛化。这不仅提升了模型的可信度，也为模型的优化提供了方向。

# 6. 数据预处理综合案例分析

## 6.1 案例一：信用卡欺诈检测

### 6.1.1 数据集简介与预处理需求

信用卡欺诈检测是金融安全领域的一个重要问题。在处理此类数据集时，预处理步骤显得尤为重要，因为它们直接关系到模型的检测效果。此数据集可能包含诸如交易金额、交易时间、用户历史交易行为等敏感信息。预处理需求包括数据清洗、异常值处理、数据标准化和归一化，以及特征编码等步骤。

### 6.1.2 预处理步骤与模型性能提升

在信用卡欺诈检测中，我们可以按照以下步骤进行数据预处理：

1. **数据清洗**：检查并处理缺失值和异常值。例如，如果交易金额出现负值，这可能表示数据录入错误或欺诈行为，需要进一步调查。

2. **特征选择**：选取与欺诈检测高度相关的特征，如用户历史交易的平均金额、交易频率等。

3. **数据转换**：将类别特征转换为数值形式，例如使用独热编码（One-Hot Encoding）来处理布尔值特征。

4. **数据标准化和归一化**：使用标准化方法如Z-score或归一化方法如MinMaxScaler将特征缩放到统一的范围内。

5. **特征工程**：构造新的特征，如交易金额与交易时间的关系，或者用户的消费习惯特征。

6. **模型训练与评估**：在预处理后，使用适当的机器学习模型进行训练，并使用交叉验证等方法进行模型评估。

通过预处理步骤，不仅提高了数据质量，还增强了模型的预测能力，有效识别出可能的欺诈行为。

## 6.2 案例二：文本分类

### 6.2.1 文本预处理流程

文本数据通常包含大量的噪声，例如标点符号、停用词、大小写不一致等，因此需要进行严格的预处理。文本分类的预处理流程包括以下步骤：

1. **分词**：将文本拆分成有意义的单元（单词、短语或符号）。

2. **去除停用词**：删除文本中的常见词汇，如“的”、“和”、“是”等。

3. **文本清洗**：去除标点符号、特殊字符，统一大小写。

4. **词干提取**或**词形还原**：将词汇转换为其基本形式。

5. **词向量表示**：将清洗后的文本转换成数值向量，常用方法有TF-IDF和Word2Vec。

### 6.2.2 预处理后的模型性能分析

在完成文本预处理后，可以使用不同的算法进行文本分类任务。例如，朴素贝叶斯、支持向量机（SVM）、随机森林或深度学习模型。对于向量化的文本数据，深度学习模型如卷积神经网络（CNN）和循环神经网络（RNN）尤其有效。预处理后的文本数据对模型性能有显著影响：

- **准确率提升**：通过去除噪声和标准化文本格式，模型能够更准确地学习文本数据的特征。
- **训练时间缩短**：有效的预处理能减少模型处理的数据量，从而缩短训练时间。

## 6.3 案例三：图像识别问题

### 6.3.1 图像数据预处理技术

图像识别任务需要处理大量的图像数据，而图像数据预处理是提高模型性能的关键步骤。常见的图像预处理技术包括：

1. **缩放**：将所有图像调整到统一大小。

2. **归一化**：对像素值进行归一化处理，使其落在一个小的区间内，如[0, 1]。

3. **数据增强**：通过旋转、翻转、裁剪等技术增加训练数据的多样性。

4. **标准化**：对图像进行标准化处理，消除光照等外部条件带来的影响。

### 6.3.2 预处理对模型性能的影响

图像数据的预处理对模型性能有着直接影响。通过预处理：

- **改善泛化能力**：数据增强技术可显著提升模型的泛化能力，避免过拟合。

- **提高准确率**：标准化和归一化能够加快模型的收敛速度，提高训练的稳定性和最终的识别准确率。

- **减少计算复杂度**：适当的数据预处理可减少计算资源的使用，优化训练过程。

在实际应用中，预处理步骤需要根据具体问题和数据集的特点进行调整，以达到最优的模型性能。