双曲正弦函数逆函数揭秘：探索性质与应用

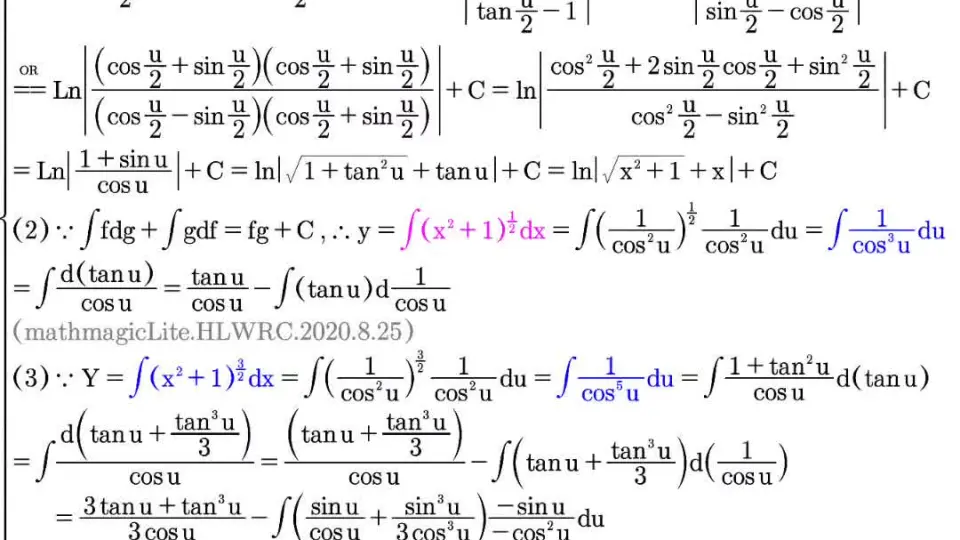
# 1. 双曲正弦函数逆函数简介

双曲正弦函数逆函数，记作 `arsinh(x)`，是双曲正弦函数 `sinh(x)` 的反函数。它表示为：

arsinh(x) = ln(x + sqrt(x^2 + 1))

其中 `ln` 表示自然对数。双曲正弦函数逆函数将实数映射到实数，其定义域为实数集，值域为实数集。

# 2. 双曲正弦函数逆函数的性质

双曲正弦函数逆函数（sinh^-1）具有以下性质：

### 2.1 基本性质

#### 2.1.1 定义域和值域

双曲正弦函数逆函数的定义域为实数集 R，值域为实数集 R。

#### 2.1.2 奇偶性和周期性

双曲正弦函数逆函数是奇函数，即对于任意实数 x，有 sinh^-1(-x) = -sinh^-1(x)。

双曲正弦函数逆函数是非周期函数，即对于任意非零实数 T，不存在任何实数 x 使得 sinh^-1(x + T) = sinh^-1(x)。

### 2.2 与其他函数的关系

#### 2.2.1 与双曲正弦函数的关系

双曲正弦函数逆函数与双曲正弦函数之间的关系如下：

sinh(sinh^-1(x)) = x
sinh^-1(sinh(x)) = x

#### 2.2.2 与其他双曲函数的关系

双曲正弦函数逆函数与其他双曲函数之间的关系如下：

cosh(sinh^-1(x)) = sqrt(1 + x^2)
tanh(sinh^-1(x)) = x / sqrt(1 + x^2)
coth(sinh^-1(x)) = sqrt(1 + x^2) / x
sech(sinh^-1(x)) = 1 / sqrt(1 + x^2)
csch(sinh^-1(x)) = 1 / x

**代码块：**

import numpy as np

# 计算双曲正弦函数逆函数
def sinh_inv(x):
    return np.arcsinh(x)

# 计算双曲正弦函数
def sinh(x):
    return (np.exp(x) - np.exp(-x)) / 2

# 计算双曲余弦函数
def cosh(x):
    return (np.exp(x) + np.exp(-x)) / 2

# 计算双曲正切函数
def tanh(x):
    return sinh(x) / cosh(x)

# 计算双曲余切函数
def coth(x):
    return cosh(x) / sinh(x)

# 计算双曲正割函数
def sech(x):
    return 1 / cosh(x)

# 计算双曲余割函数
def csch(x):
    return 1 / sinh(x)

# 测试
x = np.linspace(-1, 1, 100)
y_sinh_inv = sinh_inv(x)
y_sinh = sinh(x)
y_cosh = cosh(x)
y_tanh = tanh(x)
y_coth = coth(x)
y_sech = sech(x)
y_csch = csch(x)

# 绘制图形
import matplotlib.pyplot as plt
plt.plot(x, y_sinh_inv, label="sinh^-1(x)")
plt.plot(x, y_sinh, label="sinh(x)")
plt.plot(x, y_cosh, label="cosh(x)")
plt.plot(x, y_tanh, label="tanh(x)")
plt.plot(x, y_coth, label="coth(x)")
plt.plot(x, y_sech, label="sech(x)")
plt.plot(x, y_csch, label="csch(x)")
plt.legend()
plt.show()

**逻辑分析：**

这段代码使用 NumPy 库计算双曲正弦函数逆函数、双曲正弦函数、双曲余弦函数、双曲正切函数、双曲余切函数、双曲正割函数和双曲余割函数的值。然后，使用 Matplotlib 库绘制这些函数的图形。

**参数说明：**

* `x`: 输入值，可以是标量或数组。
* `y_sinh_inv`: 双曲正弦函数逆函数的值。
* `y_sinh`: 双曲正弦函数的值。
* `y_cosh`: 双曲余弦函数的值。
* `y_tanh`: 双曲正切函数的值。
* `y_coth`: 双曲余切函数的值。
* `y_sech`: 双曲正割函数的值。
* `y_csch`: 双曲余割函数的值。

# 3. 双曲正弦函数逆函数的求解

### 3.1 解析求解方法

#### 3.1.1 泰勒展开法

泰勒展开法是一种将函数近似为多项式的技术。对于双曲正弦函数逆函数，其泰勒展开式为：

sinh^{-1}(x) = x - \frac{x^3}{3} + \frac{3x^5}{10} - \frac{5x^7}{42} + \cdots

其中，x 是自变