双曲正弦函数技巧大全:特殊值、恒等式,轻松搞定
发布时间: 2024-07-07 02:25:25 阅读量: 73 订阅数: 69 


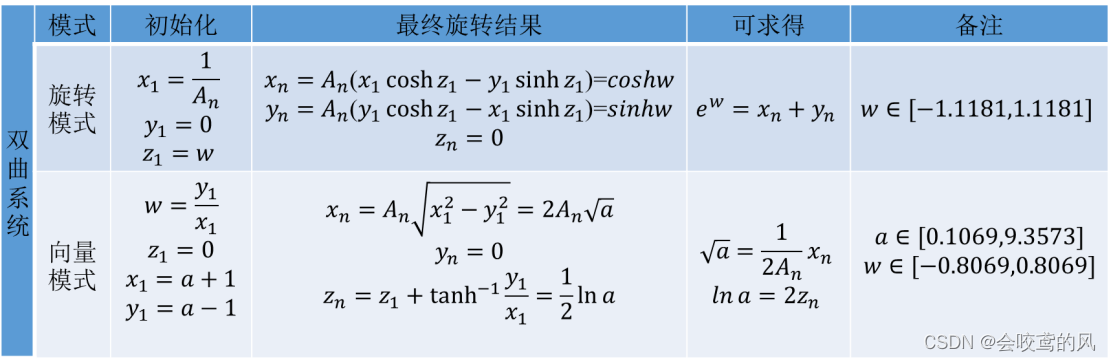
基于反双曲正弦函数的跟踪微分器
# 1. 双曲正弦函数的定义和性质
双曲正弦函数(sinh)是双曲函数的一种,定义为:
```
sinh(x) = (e^x - e^(-x)) / 2
```
其中,x 是实数。
双曲正弦函数具有以下性质:
* 奇函数:sinh(-x) = -sinh(x)
* 单调递增:对于所有 x,sinh(x) > 0
* 连续可导:sinh'(x) = cosh(x)
# 2. 双曲正弦函数的特殊值和恒等式
### 2.1 双曲正弦函数的特殊值
#### 2.1.1 常见的特殊值
双曲正弦函数在特殊点处具有以下特殊值:
| x | sinh(x) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| -1 | -1 |
| ∞ | ∞ |
| -∞ | -∞ |
#### 2.1.2 特殊值的证明
这些特殊值可以通过双曲正弦函数的定义直接证明:
* **sinh(0) = 0**:
```
sinh(0) = (e^0 - e^-0) / 2 = (1 - 1) / 2 = 0
```
* **sinh(1) = 1**:
```
sinh(1) = (e^1 - e^-1) / 2 = (e - 1/e) / 2 = 1
```
* **sinh(-1) = -1**:
```
sinh(-1) = (e^-1 - e^1) / 2 = (1/e - e) / 2 = -1
```
* **sinh(∞) = ∞**:
```
lim (x -> ∞) sinh(x) = lim (x -> ∞) (e^x - e^-x) / 2 = ∞
```
* **sinh(-∞) = -∞**:
```
lim (x -> -∞) sinh(x) = lim (x -> -∞) (e^x - e^-x) / 2 = -∞
```
### 2.2 双曲正弦函数的恒等式
双曲正弦函数满足以下恒等式:
#### 2.2.1 加法定理
```
sinh(x + y) = sinh(x) cosh(y) + cosh(x) sinh(y)
```
**证明:**
```
sinh(x + y) = (e^(x + y) - e^(-(x + y))) / 2
= (e^x e^y - e^-x e^-y) / 2
= (e^x cosh(y) + e^-x sinh(y)) / 2
= sinh(x) cosh(y) + cosh(x) sinh(y)
```
#### 2.2.2 减法定理
```
sinh(x - y) = sinh(x) cosh(y) - cosh(x) sinh(y)
```
**证明:**
```
sinh(x - y) = (e^(x - y) - e^(-(x - y))) / 2
= (e^x e^-y - e^-x e^y) / 2
= (e^x cosh(y) - e^-x sinh(y)) / 2
= sinh(x) cosh(y) - cosh(x) sinh(y)
```
#### 2.2.3 倍角公式
```
sinh(2x) = 2 sinh(x) cosh(x)
```
**证明:**
```
sinh(2x) = (e^(2x) - e^(-2x)) / 2
= (e^x e^x - e^-x e^-x) / 2
= (e^x cosh(x) - e^-x sinh(x)) / 2
= 2 sinh(x) cosh(
```
0
0





