双曲正弦函数的逆函数之旅：揭示其反函数的秘密

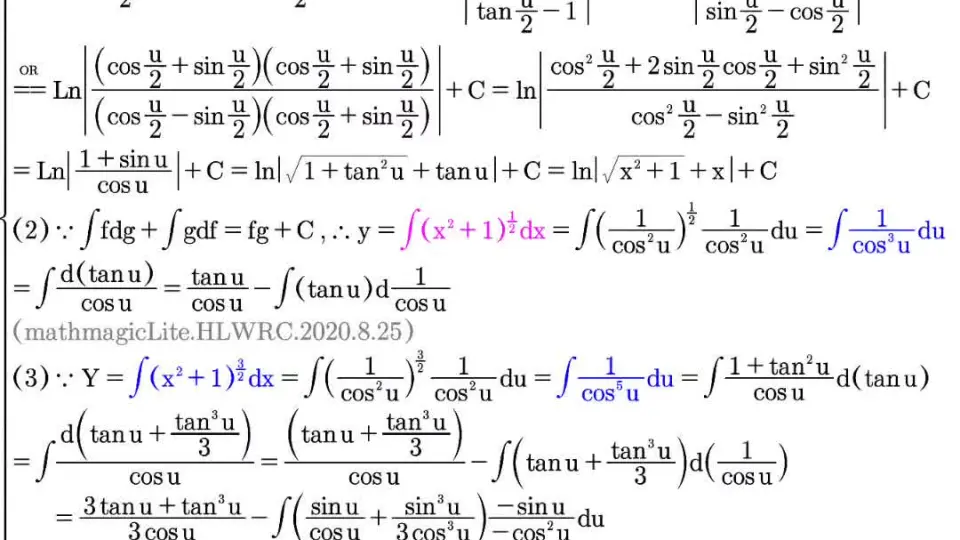
# 1. 双曲正弦函数的数学基础

双曲正弦函数（sinh）是双曲函数家族中的一种，与三角函数中的正弦函数类似。它的定义为：

sinh(x) = (e^x - e^(-x)) / 2

其中，e是自然对数的底数。

双曲正弦函数具有以下性质：

* 奇函数：sinh(-x) = -sinh(x)
* 单调递增：x > 0时，sinh(x) > 0；x < 0时，sinh(x) < 0
* 导数：d/dx sinh(x) = cosh(x)
* 积分：∫sinh(x) dx = cosh(x) + C

# 2. 双曲正弦函数的逆函数探索

### 2.1 逆双曲正弦函数的定义和性质

#### 2.1.1 逆双曲正弦函数的定义

逆双曲正弦函数，记为 `arsinh(x)`，是双曲正弦函数 `sinh(x)` 的逆函数。它定义为：

arsinh(x) = y ⇔ sinh(y) = x

其中，`x` 和 `y` 是实数。

#### 2.1.2 逆双曲正弦函数的性质

逆双曲正弦函数具有以下性质：

* **单调递增：** `arsinh(x)` 对于所有实数 `x` 都是单调递增的。
* **奇函数：** `arsinh(-x) = -arsinh(x)`。
* **恒等式：** `sinh(arsinh(x)) = x`，`arsinh(sinh(x)) = x`。
* **导数：** `d/dx arsinh(x) = 1 / sqrt(x^2 + 1)`。
* **积分：** `∫ arsinh(x) dx = x arsinh(x) - sqrt(x^2 + 1) + C`。

### 2.2 逆双曲正弦函数的求导和积分

#### 2.2.1 逆双曲正弦函数的求导

逆双曲正弦函数的导数可以用以下公式计算：

d/dx arsinh(x) = 1 / sqrt(x^2 + 1)

**证明：**

使用隐函数求导法：

sinh(arsinh(x)) = x

两边对 `x` 求导：

cosh(arsinh(x)) * d/dx arsinh(x) = 1

由于 `cosh(x) = sqrt(sinh^2(x) + 1)`，因此：

sqrt(sinh^2(arsinh(x)) + 1) * d/dx arsinh(x) = 1

代入 `sinh(arsinh(x)) = x`：

sqrt(x^2 + 1) * d/dx arsinh(x) = 1

因此：

d/dx arsinh(x) = 1 / sqrt(x^2 + 1)

#### 2.2.2 逆双曲正弦函数的积分

逆双曲正弦函数的积分可以用以下公式计算：

∫ arsinh(x) dx = x arsinh(x) - sqrt(x^2 + 1) + C

其中，`C` 是积分常数。

**证明：**

使用分部积分法：

u = arsinh(x), dv = dx

则：

du = 1 / sqrt(x^2 + 1) dx, v = x

因此：

∫ arsinh(x) dx = x arsinh(x) - ∫ x / sqrt(x^2 + 1) dx

令 `y = x^2 + 1`，则 `dy = 2x dx`：

∫ arsinh(x) dx = x arsinh(x) - ∫ 1 / sqrt(y) * 1/2 dy

∫ arsinh(x) dx = x arsinh(x) - sqrt(y) + C

代回 `y = x^2 + 1`：

∫ arsinh(x)