双曲正弦函数在数学建模中的力量：解决现实世界问题的利器

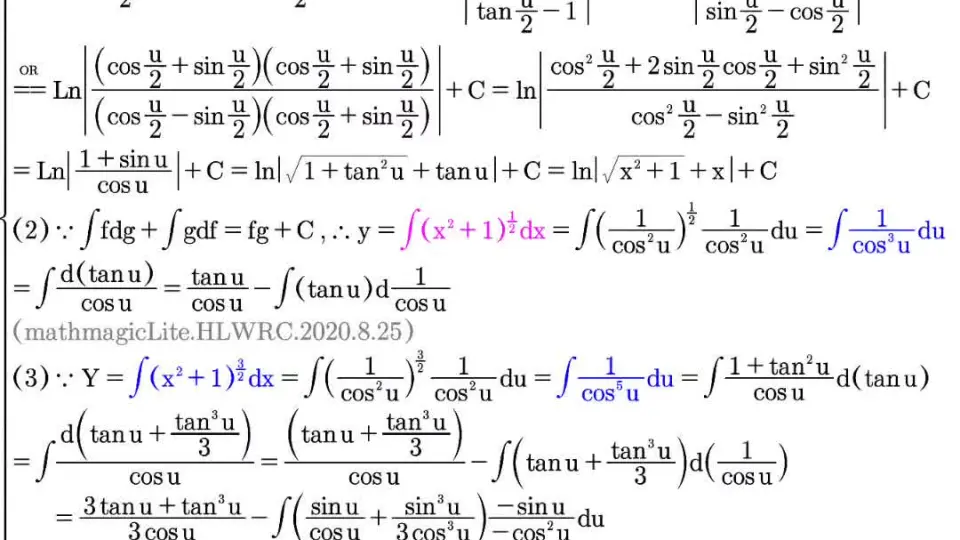
# 1. 双曲正弦函数的理论基础

双曲正弦函数（sinh），是双曲函数族中的一种，其定义为：

sinh(x) = (e^x - e^-x) / 2

它与正弦函数类似，但具有不同的图像和性质。双曲正弦函数的图像是一条双曲线，在原点处对称。其导数为cosh(x)，积分结果为cosh(x) + C。

双曲正弦函数在数学和科学中有着广泛的应用，例如：

* **物理建模：**弹簧振动、热传导等物理现象
* **生物建模：**种群增长、药物动力学等生物过程

# 2. 双曲正弦函数的建模技巧

### 2.1 单变量建模

**2.1.1 拟合非线性数据**

双曲正弦函数可以用来拟合非线性数据，例如指数增长或衰减。拟合过程涉及找到函数参数，使其曲线与数据点最接近。

import numpy as np
import matplotlib.pyplot as plt

# 数据点
x = np.linspace(0, 10, 100)
y = np.exp(-x)

# 拟合双曲正弦函数
from scipy.optimize import curve_fit

def func(x, a, b):
    return a * np.sinh(b * x)

popt, pcov = curve_fit(func, x, y)
a, b = popt

# 绘制拟合曲线
plt.plot(x, y, 'o')
plt.plot(x, func(x, a, b), '-')
plt.show()

**逻辑分析：**

* `scipy.optimize.curve_fit` 函数用于拟合非线性数据。
* `func` 函数定义了双曲正弦函数模型。
* `popt` 和 `pcov` 分别包含拟合参数和协方差矩阵。
* `a` 和 `b` 是拟合的双曲正弦函数参数。

**2.1.2 预测时间序列**

双曲正弦函数还可以用于预测时间序列，即随时间变化的数据。预测过程涉及使用历史数据训练模型，然后使用模型预测未来的值。

import pandas as pd
import statsmodels.api as sm

# 时间序列数据
df = pd.read_csv('time_series.csv')
df['date'] = pd.to_datetime(df['date'])
df.set_index('date', inplace=True)

# 训练双曲正弦函数模型
model = sm.tsa.statespace.ExponentialSmoothing(df['value'], trend='add', seasonal=None).fit()

# 预测未来值
forecast = model.forecast(steps=12)

# 绘制实际值和预测值
plt.plot(df['value'], label='Actual')
plt.plot(forecast, label='Forecast')
plt.legend()
plt.show()

**逻辑分析：**

* `statsmodels.ap