决策树剪枝技术案例研究

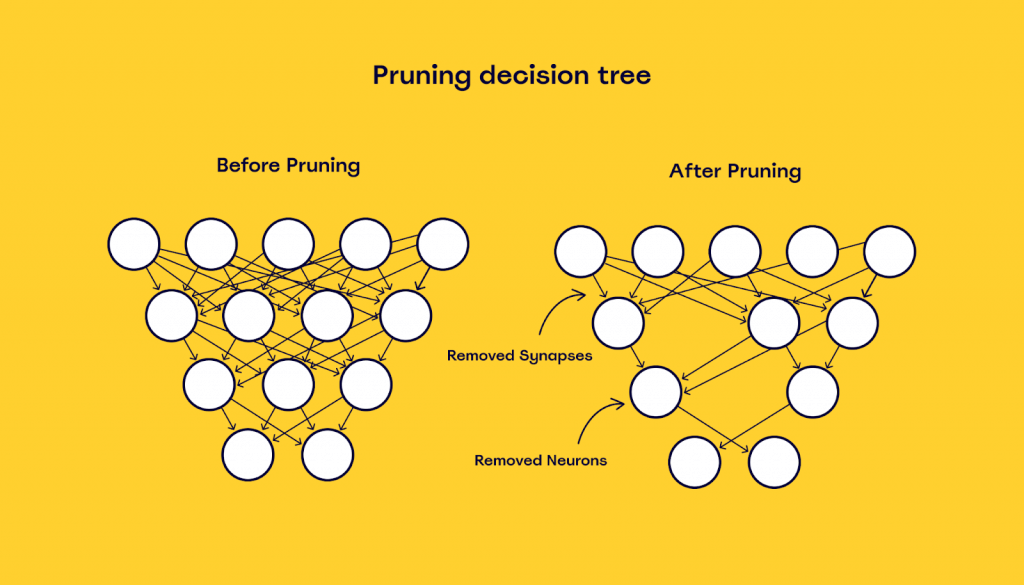
# 1. 决策树剪枝技术概述

## 1.1 决策树剪枝概念

决策树剪枝是一种机器学习中的模型优化技术，用于改进决策树模型的泛化能力，防止过拟合。其核心思想在于在保证模型准确度的同时，减小树的复杂性，提升模型的泛化性能。

## 1.2 剪枝的必要性

在构建决策树的过程中，树往往倾向于学习训练数据中的噪声，导致模型在未见过的数据上表现不佳。因此，适时的剪枝能够移除这些不必要的分支，使得模型变得更加稳定和健壮。

## 1.3 剪枝技术的分类

剪枝技术可以分为预剪枝和后剪枝。预剪枝是在树构建的过程中提前停止树的增长，而后剪枝则是在树构建完成后，通过算法来移除一部分分支。两种方法各有优势，适用于不同场景。

graph TD;
    A[决策树剪枝] --> B[预剪枝];
    A --> C[后剪枝];
    B --> B1[提前停止树增长];
    C --> C1[移除不必要的分支];

预剪枝策略简单易行，但可能因停止过早而导致模型欠拟合；后剪枝虽然计算复杂度高，但通常能得到性能更优的模型。

# 2. 决策树模型的理论基础

### 2.1 决策树的构建原理

#### 2.1.1 信息增益与熵的概念

决策树是一种基于树形结构来进行决策的算法，它的核心在于从数据集中学习出简单的决策规则。构建决策树的关键步骤之一是选择最佳的分裂属性，而选择的标准之一就是信息增益（Information Gain）。信息增益是基于熵（Entropy）的概念，它衡量了一个随机变量不确定性的减少程度。

熵是信息论中用于度量信息量的一个概念，它表示了一个随机变量的不确定性。在决策树中，熵用作分类前后的不纯度的度量。给定一个数据集，其中包含N个类别的样本，其熵的定义为：

Entropy(S) = -Σ(p_i * log2(p_i))

其中，`p_i` 是数据集中第i个类别出现的概率，S是样本集合。熵的值越高表示数据集的不确定性越大，即数据集的类别分布越不均匀。

信息增益可以定义为集合S的熵与其分割后的子集熵的期望之差：

Information Gain(S, A) = Entropy(S) - Σ( |S_v| / |S| * Entropy(S_v) )

这里，`A` 是被测试的属性，`S_v` 是属性`A`取值为`v`时`S`的子集。信息增益越大，意味着按照属性`A`进行分裂将使得数据集的不确定性减少得越多。

#### 2.1.2 决策树的分裂标准和算法

决策树的分裂标准是用来决定如何划分数据集的，最常用的分裂标准包括信息增益、增益率（Gain Ratio）和基尼指数（Gini Index）。

**信息增益**已经在上一节中介绍，但其缺点在于它偏向于选择具有更多值的属性。

**增益率**是对信息增益的一种改进，它试图解决这个问题，通过考虑属性的分裂信息（Split Information）来惩罚具有更多值的属性：

Gain Ratio(S, A) = Information Gain(S, A) / Split Information(S, A)

其中，分裂信息是对分裂后的子集大小的度量。

**基尼指数**是一种基于概率的度量，用来衡量数据集的不纯度：

Gini Index(S) = 1 - Σ(p_i^2)

选择基尼指数最小的属性作为分裂标准，可以使决策树倾向于创建“纯”的子节点。

构建决策树的常用算法包括ID3、C4.5和CART。ID3算法使用信息增益作为分裂标准，C4.5是ID3的改进版本使用增益率，而CART算法则使用基尼指数。

### 2.2 过拟合与模型泛化能力

#### 2.2.1 过拟合的定义和影响

过拟合是指模型在训练数据上表现良好，但在未见数据上表现较差的现象。过拟合的模型学习了训练数据中的噪声和异常值，从而丧失了泛化到新数据的能力。在决策树模型中，过拟合通常表现为树的高度过大，每个叶节点都只包含少数训练样本，这样的决策树过于复杂，容易导致过拟合。

过拟合的影响包括：

- **模型泛化能力下降**：模型在训练集上的性能无法被复制到新的数据集上。
- **决策树难以解释**：复杂决策树难以被解释，这违背了决策树的一个主要优点。
- **模型推广性差**：过拟合的模型无法适应新的数据，因而无法进行有效的推广。

为了解决过拟合问题，剪枝技术被引入决策树的学习过程中。

#### 2.2.2 评估模型泛化能力的方法

评估模型泛化能力的方法包括交叉验证、AUC-ROC曲线、混淆矩阵等。其中交叉验证是评估模型泛化能力的一种常用方法，它将数据集分为k份，其中一份作为验证集，其余作为训练集，循环进行k次，每次选择不同的验证集，最终计算平均性能指标。

- **k折交叉验证**是最常用的交叉验证方法。它可以减少模型评估的方差，确保模型在不同子集上具有稳定的性能。

- **AUC-ROC曲线**（Area Under the Curve - Receiver Operating Characteristic）用于评估二分类问题的模型性能。AUC值越接近于1，模型的性能越好。

- **混淆矩阵**（C