剪枝算法比较研究

1. 剪枝算法概述

在机器学习与数据分析的世界中，剪枝算法是减少模型复杂度和防止过拟合的重要技术之一。剪枝算法通过去除决策树、神经网络等模型中的冗余部分，能够显著提升模型的泛化能力。本章将对剪枝算法进行一个简要的概述，为读者提供一个整体的了解，为进一步深入探讨奠定基础。

1.1 简介

剪枝算法是一种后处理技术，它在模型训练完成后，通过特定的方法识别并去除模型中对预测贡献较小的部分。在决策树模型中，剪枝可以减少树的大小，提高其运行速度，同时减少对训练数据的依赖。在神经网络中，剪枝能够删除不重要的连接，简化网络结构，加快推理速度，并减少所需的计算资源。

1.2 剪枝算法的重要性

剪枝算法的重要性在于它能够在保持模型性能的同时，降低模型的复杂度。这在很多应用场景中至关重要，如在移动设备或嵌入式系统中，资源受限，需要运行快速且高效的模型。通过剪枝，可以使得大型模型小型化，从而适应资源有限的环境。此外，剪枝后的模型也更容易解释，有助于模型的可解释性和透明度。

1.3 剪枝算法的常见类型

剪枝算法主要分为预剪枝（pre-pruning）和后剪枝（post-pruning）。预剪枝是在构建决策树的同时进行剪枝，通过设置参数限制树的生长深度或分裂节点的最小样本数等方式来避免过拟合。后剪枝则是在决策树完全生长后，再根据特定标准来剪去不必要的节点。预剪枝简单直接，但可能剪枝过早；后剪枝能更精确地评估节点的重要性，但计算成本较高。

随着深度学习的兴起，剪枝技术也逐渐应用于神经网络的优化中，通过去除权重较小的神经元或连接，不仅加快模型的推理速度，还能减少模型的存储需求，这对于云计算资源优化和边缘计算非常有帮助。剪枝算法的发展，不仅提升了模型的效率，也促进了机器学习技术的进一步应用和普及。

2. 剪枝算法的理论基础

2.1 剪枝算法的基本概念

2.1.1 定义与分类

剪枝算法是一种在数据科学和机器学习领域广泛使用的优化技术。它主要被用于简化模型复杂度，通过去除决策树中的一些分支来防止过拟合现象。简而言之，剪枝算法通过删除一些不太重要或者冗余的部分，帮助模型专注于更有代表性的特征和模式。

在分类上，剪枝可以分为两类：预剪枝（Pre-pruning）和后剪枝（Post-pruning）。预剪枝是在训练过程中提前终止决策树的生长，而后剪枝则是在决策树完全生长后通过特定策略去除掉一些分支。预剪枝较为简单且容易实现，而后剪枝则能更好地控制模型复杂度，但计算成本更高。

2.1.2 剪枝算法在决策树中的应用

在决策树模型中，剪枝技术可以帮助我们避免产生过分复杂的树形结构，这会导致模型无法很好地泛化到新的数据上。一个典型的剪枝过程如下：

先构建一个完整的决策树，此时可能会包含一些不必要的节点和边。
应用剪枝算法，逐步检查树的每个节点，计算如果去掉该节点对预测准确性的影响。
如果去掉该节点对准确性没有显著影响或有正面影响（例如减少过拟合），则移除该节点及其相关子树。
经过多次迭代，最终得到一个简化版的决策树。

在实践中，为了评估剪枝效果，我们通常采用交叉验证的方法来测试模型在验证集上的表现。如果剪枝后的模型在验证集上的表现有显著提升，则证明剪枝过程是有益的。

2.2 剪枝策略的数学模型

2.2.1 损失函数与剪枝标准

剪枝算法的核心是损失函数（Cost Function）。在决策树中，常用的损失函数有信息增益、Gini指数等。剪枝策略的核心目标是找到一个最优的树结构，使得在损失函数上达到最小化。

损失函数通常会考虑两个方面：

纯度的提升，即数据集的分割是否能更好地进行分类。
树的复杂度，即树的大小和节点的深度。

剪枝标准则根据损失函数的优化来确定。比如，我们可以设定一个阈值，只有当去掉某个节点对整体损失函数值的减少超过这个阈值时，才会考虑剪枝。

2.2.2 正则化与剪枝的关系

正则化（Regularization）在机器学习中用于防止过拟合，增加模型的泛化能力。剪枝可以看作是一种特定形式的正则化方法，它通过限制模型的复杂度来达到减少过拟合的目的。正则化通常引入额外的惩罚项到损失函数中，例如L1正则化（Lasso回归）和L2正则化（Ridge回归）。

在决策树剪枝中，我们可以将正则化参数看作是损失函数的一个组成部分。当正则化参数增大时，模型会更倾向于选择简单但泛化能力强的结构，这就是通过正则化来实现剪枝效果。

2.3 剪枝算法的理论比较

2.3.1 算法的复杂度分析

剪枝算法的复杂度取决于所采用的具体方法，以及决策树的大小和复杂性。在最坏情况下，决策树的剪枝需要对每个节点都进行一次评估，这会带来O(n^2)的时间复杂度，其中n是树中节点的数量。

在实际应用中，剪枝操作通常可以通过一些启发式方法来加速，比如剪枝前先评估整个子树而不是单个节点，或使用近似方法来估计剪枝的影响。这些技术可以显著减少算法的运行时间，但同时可能会影响剪枝的精确性。

2.3.2 算法的收敛性质

剪枝算法的收敛性质是指算法是否能够在有限步骤内收敛到最优解。理论研究表明，后剪枝算法通常具有良好的收敛性质。这是因为后剪枝是在决策树完全生长之后进行，理论上可以通过系统地评估每个可能的剪枝操作来找到最佳的树结构。

相比之下，预剪枝可能因为停止条件设置不当而提前终止了树的生长，有可能错过最优解。然而，由于预剪枝可以显著减少计算量，实际应用中仍经常被使用，尤其当处理大数据集时。

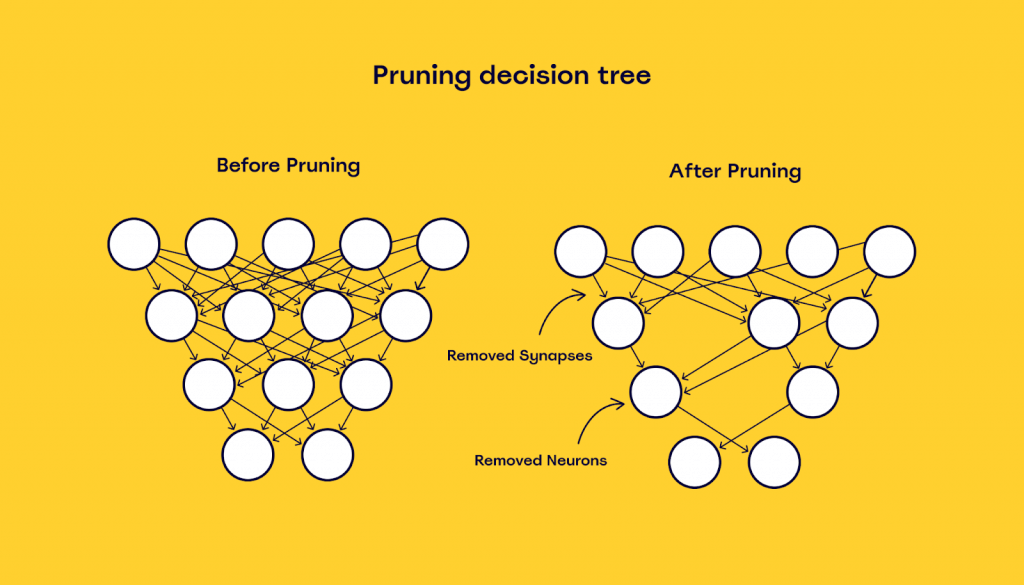
为了提供一个更为直观的理解，下面展示了一个决策树剪枝前后的对比图。左侧展示了一个未经剪枝的复杂决策树，右侧则是经过剪枝优化后的简化模型。

最低0.47元/天解锁专栏

买1年送3月

点击查看下一篇

百万级高质量VIP文章无限畅学

千万级优质资源任意下载

C知道免费提问 ( 生成式Al产品 )

剪枝算法比较研究

1. 剪枝算法概述

1.1 简介

1.2 剪枝算法的重要性

1.3 剪枝算法的常见类型