决策树剪枝对模型性能影响分析

# 1. 决策树剪枝的基本概念与原理

## 决策树剪枝的基本概念
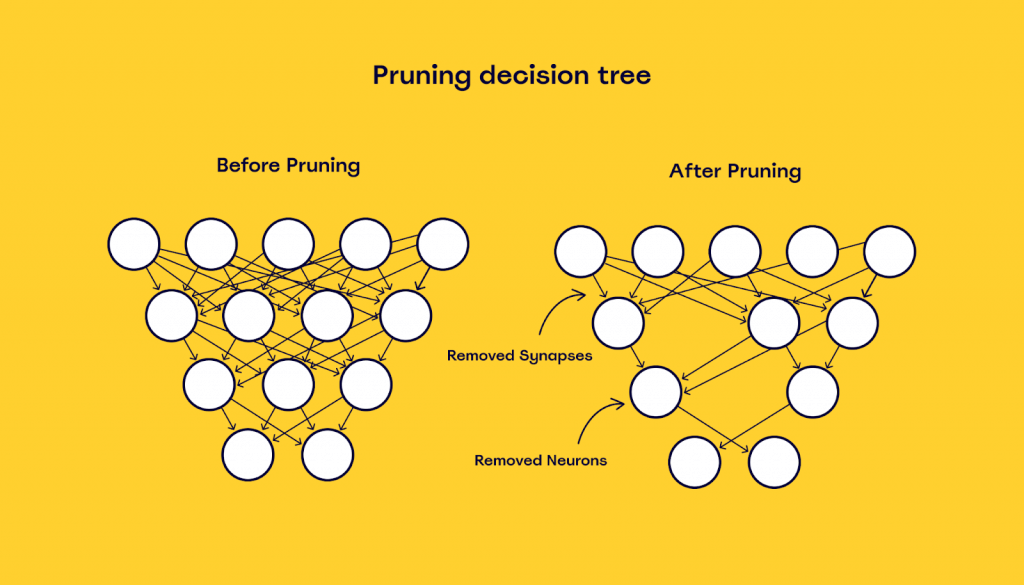
决策树剪枝是一种避免过拟合的技术，用于提高决策树模型的泛化能力。基本思想是在保留重要决策规则的同时，去除一些不重要的枝叶。它通过删除决策树中的一部分分支或叶子节点，以简化模型的复杂性，防止模型在训练数据上表现出色而在新数据上表现不佳。

## 决策树剪枝的原理
剪枝的核心在于识别并移除那些对预测结果贡献较小的决策节点，其依据是通过特定的剪枝标准评估各个节点的重要性。一个常用的剪枝标准是基于误差估计，即通过在验证集上的性能来确定哪些节点应该被剪掉。这可以减少模型的复杂性，并提高其在未见数据上的预测准确性。

## 决策树剪枝的优点
剪枝技术的优点包括：
1. **减少过拟合**：避免模型对训练数据的过度拟合，提高模型的泛化能力。
2. **提高泛化性能**：简化模型结构，减少模型复杂度，增强模型在新数据集上的表现。
3. **节省计算资源**：通过减少树的大小，可以降低模型的内存消耗和预测时间。

通过决策树剪枝，我们可以构建出既准确又高效的数据挖掘模型，这对于实际应用中的大数据处理尤为重要。在后续章节中，我们将深入探讨决策树剪枝的理论基础，包括各种剪枝策略、数学原理、以及剪枝算法的实证分析。

# 2. 决策树剪枝的理论基础

### 2.1 决策树剪枝的必要性分析

在构建决策树模型的过程中，我们往往会遇到过拟合问题。过拟合意味着模型在训练数据上表现得过于完美，而在未见过的新数据上表现则不尽如人意。为了提高模型的泛化能力，剪枝成为了一种重要的技术手段。

#### 2.1.1 过拟合问题的介绍

过拟合（Overfitting）是指模型对训练数据的特定特性学习得太好，以至于捕捉到了数据中的噪声和随机误差，而忽视了数据的潜在规律。这导致模型对新样本的预测能力下降，具体表现在以下几个方面：

- 在训练集上达到很高的准确率，但在验证集或者测试集上的表现明显下降。
- 模型的决策边界过于复杂，导致模型在新数据上的推广能力弱。
- 在某些极端情况下，过拟合的模型可能会捕捉到数据采集过程中的偶然现象，而不是背后的真实规律。

#### 2.1.2 剪枝对于过拟合的抑制作用

剪枝是一种在决策树训练过程中减少模型复杂度的方法。它通过去掉一些子树，剪掉决策树上不必要的节点，来简化模型，从而增加模型的泛化能力。剪枝方法主要包括预剪枝（Prepruning）和后剪枝（Postpruning）：

- 预剪枝是早期停止决策树的生长。在树的构建过程中，当满足某些条件（如节点的纯度超过某个阈值）时就停止树的生长。
- 后剪枝则是先完整地生成一棵决策树，然后从下到上（或者从上到下）对树的非叶节点进行评估，将那些对最终分类结果影响较小的节点剪掉。

剪枝不仅可以减少模型的复杂度，还可以避免过拟合。通过对决策树的剪枝，我们可以得到一个结构更为简洁、规则性更强的模型，从而在新数据上得到更好的预测效果。

### 2.2 剪枝策略的分类和比较

决策树剪枝策略的选择直接影响模型的性能。预剪枝和后剪枝各有优缺点，选择合适的剪枝策略对于决策树模型至关重要。

#### 2.2.1 预剪枝与后剪枝的区别

预剪枝是在决策树生长过程中，根据某些条件提前停止树的扩展。预剪枝的优点是训练速度快，因为它减少了树的深度和分支数量。但预剪枝的缺点是容易导致欠拟合，因为它可能会提前停止树的生长，从而失去学习数据中真实模式的机会。

后剪枝则是在决策树完全生长后，对树的节点进行裁剪。后剪枝的优点是能够更准确地评估节点的重要性，通常能够得到更好的预测性能。但是，后剪枝的缺点是训练时间较长，计算量大，因为需要先生成一棵完整的树。

#### 2.2.2 各种剪枝策略的优缺点

不同的剪枝策略有着各自的特点和适用场景。以下是几种常见的剪枝策略及其优缺点：

- **成本复杂度剪枝（Cost Complexity Pruning）**
- 优点：通过计算不同复杂度下的模型误差，选择最优的剪枝点。
- 缺点：需要预先设定剪枝参数，可能需要通过交叉验证来确定。

- **悲观错误剪枝（Pessimistic Error Pruning）**
- 优点：根据测试集的统计特性进行剪枝，相对简单实用。
- 缺点：可能过于保守，剪枝效果可能不及其他方法。

- **误差还原剪枝（Error Reduction Pruning）**
- 优点：通过剪掉减少误差贡献最小的节点，可以较为直观地进行剪枝。
- 缺点：评估节点误差贡献的计算量较大，可能影响训练速度。

### 2.3 剪枝算法的数学原理

决策树剪枝算法在数学上涉及到信息增益的度量和损失函数的选择，这些原理构成了剪枝算法的核心。

#### 2.3.1 剪枝过程中的信息增益与损失函数

信息增益（Information Gain）是衡量决策树节点纯度的常用指标。在剪枝过程中，我们希望保留那些能够带来较大信息增益的节点，去掉那些信息增益较小的节点。

剪枝策略通常会选择一个损失函数（Loss Function）来衡量剪枝的效果。损失函数通常由两部分组成：一部分是训练误差，另一部分是模型复杂度的惩罚项。在剪枝过程中，我们需要找到使得损失函数最小的剪枝点。

#### 2.3.2 剪枝算法的复杂度分析

剪枝算法的复杂度分析对于评估剪枝策略的效率至关重要。一般来说，预剪枝的复杂度相对较低，因为其减少了树的生长过程，而后剪枝的复杂度较高，因为它需要对整棵树进行多次评估和剪枝。

在剪枝算法中，需要考虑以下几种复杂度：

- **时间复杂度**：指剪枝过程需要消耗的时间，通常与数据量、树的大小有关。
- **空间复杂度**：指剪枝过程中所需额外存储空间的大小，主要与树的深度和节点数有关。
- **剪枝复杂度**：指的是为了达到最优剪枝效果，需要评估的子树数量。

剪枝算法的优化往往是在保证模型性能的前提下，尽可能降低算法的复杂度，以提高计算效率。

通过分析决策树剪枝的必要性、剪枝策略的分类、以及剪枝算法的数学原理，我们可以更好地理解剪枝对于提高决策树泛化能力的重要性，并选择合适的剪枝方法来构建一个有效且高效的决策树模型。在下一章中，我们将深入探讨决策树剪枝方法在实际应用中的实证分析，以及剪枝技术在不同算法中的对比和实际数据集上的应用效果。

# 3. 决策树剪枝方法的实证分析

## 3.1 基于CART算法的剪枝实例
### 3.1.1 CART算法的剪枝原理
CART算法（Classification And Regression Trees，分类与回归树）是一种常用的决策树算法，它生成的二叉树模型适合用于分类和回归任务。CART算法的关键在于通过二叉递归分割的方式对特征空间进行划分，最终形成一个二叉树结构。在该过程中，CART算法使用“基尼指数”作为分割的不纯度度量，基尼指数越小，表示分割后子集的纯度越高。

剪枝是CART算法中非常重要的一步，它的目的是防止决策树过拟合，提高模型泛化能力。剪枝可以分为预剪枝和后剪枝。预剪枝通过提前停止树的生长来防止过拟合，而后剪枝则是在树完全生长后再通过算法去除掉一些分支，保留关键信息。

在后剪枝过程中，通常使用的是代价复杂度剪枝（Cost Complexity Pruning，也称为alpha剪枝）。此方法通过引入一个惩罚项来评估剪枝的收益和代价，公式如下：

\[ C_\alpha(T) = C(T) + \alpha|T| \]

其中 \( C(T) \) 为树 \( T \) 的误差复杂度，而 \( |T| \) 是树的大小，即节点数量；\( \alpha \) 是一个正则化参数，由交叉验证确定。

### 3.1.2 实际数据集的剪枝应用
为了演示CART算法中后剪枝的实际应用，假设我们使用Python的`scikit-learn`库来完成决策树的训练和剪枝。以下是相应的代码实现：

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 加载数据集
iris = load_iris()
X, y = iris.data, iris.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 初始化CART模型，设置最大深度
clf = DecisionTreeClassifier(max_depth=None, random_state=42)

# 训练未剪枝的决策树
clf.fit(X_train, y_train)

# 预测未剪枝的决策树结果
y_pred_ungpruned = clf.predict(X_test)
print(f"未剪枝模型的准确度: {accuracy_score(y_test, y_pred_ungpruned)}")

# 设置一系列的alpha值进行剪枝
alpha_values = [0.01, 0.02, 0.05, 0.1]
for alpha in alpha_values:
    # 使用Cost Complexity Pruning进行后剪枝
    clf_pruned = DecisionTreeClassifier(
        max_depth=None, ccp_alpha=alpha, r