AVL树：平衡二叉树的实现与旋转操作

# 1. AVL树的基本概念和特性**

AVL树（Adelson-Velsky and Landis tree）是一种平衡二叉搜索树，它通过维护每个节点的平衡因子来保证树的高度平衡。平衡因子定义为左子树的高度减去右子树的高度。AVL树的特性包括：

- 平衡性：每个节点的平衡因子绝对值不超过1。
- 搜索效率：由于树的高度平衡，在AVL树中进行搜索的时间复杂度为O(log n)，其中n是树中节点的数量。
- 插入和删除效率：AVL树的插入和删除操作通过旋转操作来维护平衡性，时间复杂度也是O(log n)。

# 2. AVL树的实现

### 2.1 AVL树的节点结构和属性

AVL树的节点结构与普通二叉搜索树类似，但增加了额外的属性来维护平衡性。每个节点包含以下属性：

- **键值（key）：**与二叉搜索树中相同，用于比较和排序。
- **左子树（left）：**指向左子树的指针。
- **右子树（right）：**指向右子树的指针。
- **高度（height）：**表示以该节点为根的子树的高度。

### 2.2 AVL树的插入操作

#### 2.2.1 插入新节点

插入操作与二叉搜索树类似，根据键值进行比较，将新节点插入到适当的位置。

def insert(self, key):
    # 递归查找插入位置
    if self.key is None:
        self.key = key
        self.height = 1
    elif key < self.key:
        if self.left is None:
            self.left = AVLTree()
        self.left.insert(key)
    else:
        if self.right is None:
            self.right = AVLTree()
        self.right.insert(key)

    # 更新高度
    self.update_height()

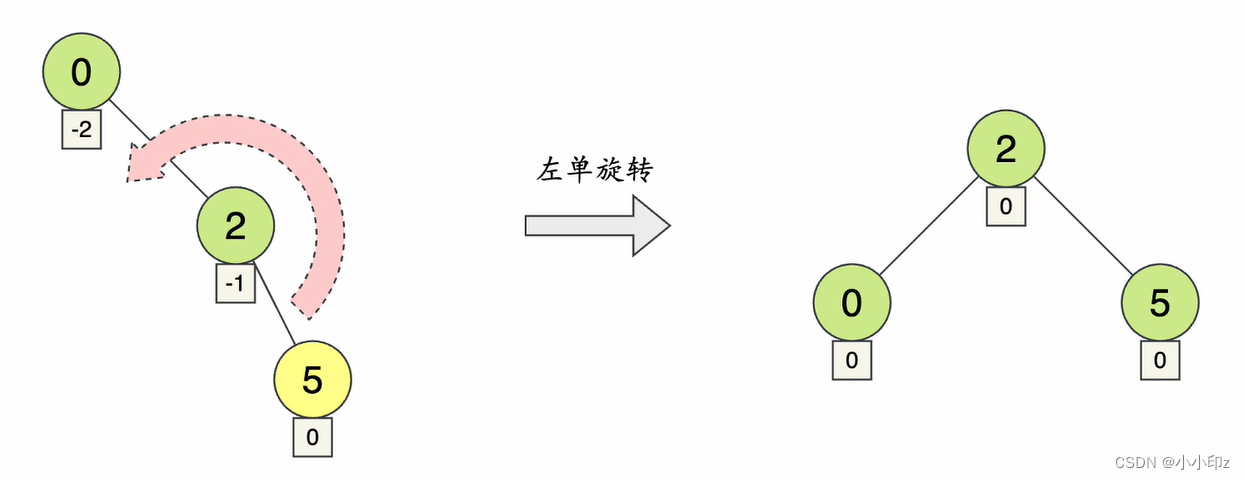
#### 2.2.2 维护平衡性：左旋和右旋

插入新节点后，需要检查树的平衡性。如果平衡因子（左子树高度 - 右子树高度）大于 1 或小于 -1，则需要进行旋转操作来恢复平衡。

**左旋操作：**当平衡因子大于 1 时，说明左子树过高，需要将左子树的右子树提升为根节点。

def left_rotate(self):
    # 获取左子树的右子树
    right_child = self.left.right

    # 将左子树的右子树提升为根节点
    self.left.right = right_child.left
    right_child.left = self.left

    # 将右子树提升为左子树
    self.left = right_child

    # 更新高度
    self.update_height()
    self.left.update_height()

**右旋操作：**当平衡因子小于 -1 时，说明右子树过高，需要将右子树的左子树提升为根节点。

def right_rotate(self):
    # 获取右子树的左子树
    left_child = self.right.left

    # 将右子树的左子树提升为根节点
    self.right.left = left_child.right
    left_child.right = self.right

    # 将左子树提升为右子树
    self.right = left_child

    # 更新高度
    self.update_height()
    self.right.update_height()

### 2.3 AVL树的删除操作

#### 2.3.1 删除节点

删除操作与二叉搜索树类似，根据键值进行比较，找到要删除的节点。

def delete(self, key):
    # 递归查找要删除的节点
    if self.key is None:
        return

    if key < self.key:
        if self.left is not None:
            self.left.delete(key)
    elif key > self.key:
        if self.right is not None:
            self.right.delete(key)
    else:
        # 找到要删除的节点
        if self.left is None and self.right is None:
            self.key = None
        elif self.left is None:
            self.key = self.right.key
            self.right = self.right.right
        elif self.right is None:
            self.key = self.left.key
            self.left = self.left.left
        else:
            # 找到右子树中的最小节点
            min_node = self.right
            while min_node.left is not None:
                min_node = min_node.left

            # 将最小节点的值替换为要删除的节点的值
            self.key = min_node.key

            # 删除最小节点
            self.right.delete(min_node.key)

    # 更新高度
    self.update_height()

#### 2.3.2 维护平衡性：左旋、右旋和双旋

删除节点后，需要检查树的平衡性。如果平衡因子大于 1 或小于 -1，则需要进行旋转操作来恢复平衡。

**左旋、右旋操作：**与插入操作中的旋转操作相同。

**双旋操作：**当平衡因子为 2 或 -2 时，说明需要进行双旋操作。双旋操作是先进行一次左旋或右旋，然后再进行一次相反方向的旋转。

def double_rotate(self, direction):
    if direction == "le