树结构简介及应用场景解析

# 1. 树结构的基本概念和特性

树结构是一种非线性数据结构，它由一系列节点组成，这些节点通过边连接在一起。树结构具有以下基本特性：

- **根节点：**树结构中只有一个根节点，它是树结构的起点。
- **子节点：**每个节点都可以拥有零个或多个子节点。
- **父节点：**每个节点除了根节点外，都有一个父节点。
- **度：**一个节点的度是指它拥有的子节点数量。
- **深度：**一个节点的深度是指从根节点到该节点的边数。
- **高度：**树结构的高度是指从根节点到最深叶节点的边数。

# 2. 树结构的理论基础

### 2.1 树的定义和术语

**定义：**

树是一种非线性数据结构，由一个称为根节点的特殊节点以及零个或多个称为子节点的节点组成。子节点可以进一步拥有自己的子节点，形成一个层次结构。

**术语：**

* **根节点：**树的起始节点，没有父节点。
* **子节点：**拥有父节点的节点。
* **父节点：**拥有子节点的节点。
* **叶节点：**没有子节点的节点。
* **深度：**从根节点到该节点的最长路径上的节点数。
* **高度：**树中从根节点到最深叶节点的最长路径上的节点数。
* **度：**一个节点拥有的子节点数。

### 2.2 树的性质和类型

**性质：**

* 树中没有环。
* 每个节点最多有一个父节点。
* 树中的节点可以按层次组织。

**类型：**

* **二叉树：**每个节点最多有两个子节点。
* **满二叉树：**每个非叶节点都有两个子节点。
* **完全二叉树：**除了最后一层外，每一层都完全填充。
* **平衡二叉树：**左右子树的高度差不大于 1。
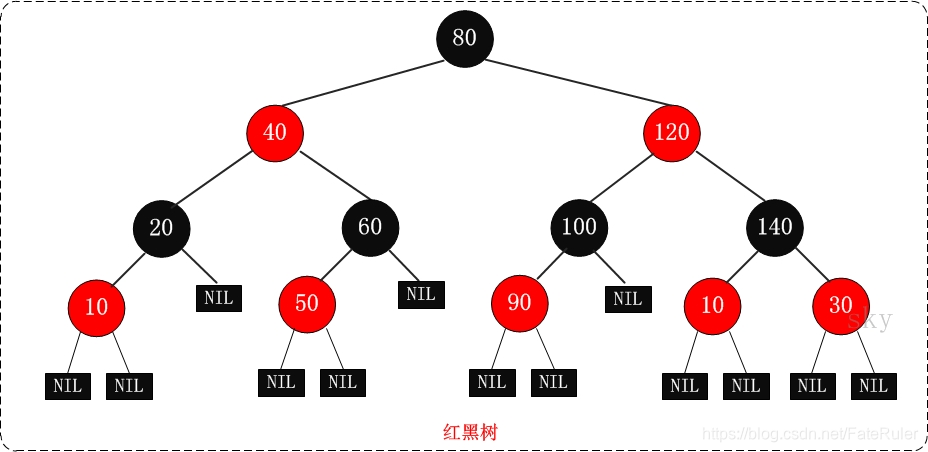
* **红黑树：**一种自平衡二叉树，具有良好的查找和插入性能。

### 2.3 树的遍历算法

遍历树有三种基本算法：

* **前序遍历：**先访问根节点，再前序遍历左子树，最后前序遍历右子树。
* **中序遍历：**先中序遍历左子树，再访问根节点，最后中序遍历右子树。
* **后序遍历：**先后序遍历左子树，再后序遍历右子树，最后访问根节点。

**代码块：**

# 前序遍历
def preorder_traversal(node):
    if node is not None:
        print(node.data)
        preorder_traversal(node.left)
        preorder_traversal(node.right)

# 中序遍历
def inorder_traversal(node):
    if node is not None:
        inorder_traversal(node.left)
        print(node.data)
        inorder_traversal(node.right)

# 后序遍历
def postorder_traversal(node):
    if node is not None:
        postorder_traversal(node.left)
        postorder_traversal(node.right)
        print(node.data)

**逻辑分析：**

* 前序遍历：先访问根节点，然后依次访问左子树和右子树。
* 中序遍历：先访问左子树，然后访问根节点，最后访问右子树。
* 后序遍历：先访问左子树，然后访问右子树，最后访问根节点。

**参数说明：**

* `node`：要遍历的节点。

# 3. 树结构的应用场景

### 3.1 文件系统中的树形结构

文件系统是计算机中用于组织和管理文件的一种数据结构。它通常采用树形结构，其中根目录位于树的根部，子目录和文件作为树的子节点。

**优点：**

* **层次化组织：**树形结构允许文件和目录以层次化的方式组织，便于用户浏览和管理文件。
* **快速访问：**通过目录树导航可以快速访问文件，因为系统只需要遍历树中的路径即可找到文件。
* **扩展性：**树形结构易于扩展，可以轻松添加新的目录和文件，而不会影响现有结构。

**示例：**

Windows 和 Linux 等操作系统都使用树形结构来组织文件系统。例如，在 Windows 中，根目录为 "C:\"，用户可以创建子目录（如 "Documents"、"Pictures"）和文件。

### 3.2 数据库中的树形结构

数据库中使用树形结构来组织数据，称为层次数据库模型。在层次数据库中，数据记录以树形结构组织，其中每个记录都有一个父记录和多个子记录。

**优点：**

* **快速查询：**树形结构允许快速查询数据，因为系统可以沿着树的路径快速找到所需记录。
* **数据完整性：**层次数据库模型强制执行数据完整性，因为每个子记录都与父记录相关联，从而防止数据丢失或损坏。
* **数据导航：**树形结构便于数据导航，因为用户可以轻松地从父记录导航到子记录。

**示例：**

层次数据库模型在早期数据库系统中很常见，例如 IMS 和 DB2。然而，随着关系数据库模型的兴起，层次数据库模型的使用已大幅减少。

### 3.3 网络中的树形结构

在计算机网络中，树形结构用于组织网络拓扑。在这种结构中，根节点代表网络中的根设备（例如路由器），而子节点代表连接到根设备的设备（例如交换机、计算机）。

**优点：**

* **广播控制：**树形结构有助于控制广播流量，因为广播仅在子网中传播，不会传播到整个网络。
* **故障隔离：**如果树中的一个节点出现故障，则只影响该节点及其子节点，不会影响整个网络。
* **可扩展性：**树形结构易于扩展，可以轻松添加新的设备，而不会影响现有拓扑。

**示例：**

以太网和令牌环网络等许多网络协议都使用树形结构来组织网络拓扑。例如，在以太网中，根节点是交换机，而连接到交换机的计算机是子节点。

# 4. 树结构的实践应用

### 4.1 树结构在文件管理中的应用

#### 4.1.1 文件系统中的树形结构

文件系统是计算机系统中用于组织和管理文件的系统。树形结构在文件系统中扮演着重要的角色，它将文件和目录组织成一个层次结构。

#### 4.1.2 树形结构的优势

使用树形结构管理文件具有以下优势：

- **易于浏览和组织：**树形结构提供了直观的层次结构，使用户可以轻松浏览和组织文件。
- **高效的文件访问：**通过使用路径名，用户可以快速访问文件，而无需遍历整个文件系统。
- **文件共享：**树形结构允许用户在不同的设备和用户之间共享文件。

#### 4.1.3 树形结构的实现

文件系统中的树形结构通常使用以下数据结构实现：

- **节点：**每个节点代表一个文件或目录，包含文件名、文件大小、文件类型等信息。
- **指针：**每个节点包含指向其子节点的指针，形成一个层次结构。
- **根节点：**树形结构的根节点代表文件系统的根目录。

### 4.2 树结构在数据库管理中的应用

#### 4.2.1 数据库中的树形结构

数据库管理系统（DBMS）使用树形结构来组织和管理数据。最常见的树形结构是B树，它是一种平衡搜索树，用于高效地存储和检索数据。

#### 4.2.2 B树的结构

B树是一种多路搜索树，具有以下结构：

- **节点：**每个节点包含多个键值对，以及指向子节点的指针。
- **根节点：**B树的根节点包含最小的键值对。
- **叶节点：**B树的叶节点包含最大的键值对。
- **平衡：**B树通过分裂和合并节点来保持平衡，确保每个节点中键值对的数量大致相等。

#### 4.2.3 B树的优势

使用B树管理数据具有以下优势：

- **高效的搜索：**B树使用二分查找算法，可以快速找到特定的键值对。
- **高效的插入和删除：**B树通过分裂和合并节点，可以高效地插入和删除键值对。
- **数据完整性：**B树强制执行数据完整性规则，确保数据的一致性。

### 4.3 树结构在网络管理中的应用

#### 4.3.1 网络中的树形结构

树形结构在网络管理中用于组织和管理网络设备。最常见的树形结构是生成树协议（STP），它用于防止网络中出现环路。

#### 4.3.2 STP的结构

STP使用以下数据结构实现树形结构：

- **根桥：**网络中具有最低桥ID的交换机。
- **指定端口：**连接到根桥的端口。
- **根端口：**连接到指定端口的端口。
- **阻塞端口：**未参与生成树的端口。

#### 4.3.3 STP的优势

使用STP管理网络具有以下优势：

- **防止环路：**STP通过阻止冗余路径来防止网络中出现环路。
- **快速收敛：**STP在网络拓扑发生变化时能够快速收敛，确保网络的稳定性。
- **冗余：**STP提供冗余路径，在一条路径出现故障时，网络仍然可以正常运行。

# 5.1 树结构的优化算法

### 5.1.1 平衡二叉树

平衡二叉树是一种特殊的二叉树，其左右子树的高度差至多为 1。通过保持树的平衡，可以显著提高树的查找、插入和删除操作的效率。平衡二叉树的典型实现包括 AVL 树和红黑树。

### 5.1.2 B 树

B 树是一种多路搜索树，其每个节点可以包含多个子节点。B 树在数据库管理系统中广泛使用，因为它可以有效地存储和检索大量数据。B 树的优化算法包括 B+ 树和 B* 树。

### 5.1.3 2-3 树

2-3 树是一种特殊的平衡树，其每个节点可以包含 2 个或 3 个子节点。2-3 树的优化算法包括 2-3-4 树和 B 树。

### 5.1.4 跳表

跳表是一种随机化的数据结构，其在查找、插入和删除操作方面具有 O(log n) 的时间复杂度。跳表通过使用多个层次的链表来实现，每个层次的链表都比上一层更稀疏。

### 5.1.5 优化算法的比较

| 优化算法 | 平均时间复杂度 | 最坏时间复杂度 | 空间复杂度 |
|---|---|---|---|
| 平衡二叉树 | O(log n) | O(n) | O(n) |
| B 树 | O(log n) | O(n) | O(n) |
| 2-3 树 | O(log n) | O(n) | O(n) |
| 跳表 | O(log n) | O(n) | O(n) |

### 5.1.6 优化算法的选择

选择合适的优化算法取决于树结构的具体应用场景和性能要求。平衡二叉树适用于需要快速查找和插入操作的场景，而 B 树和 2-3 树适用于需要存储和检索大量数据的场景。跳表适用于需要快速查找和插入操作，并且数据分布相对均匀的场景。