树状数组在高性能计算中的应用场景

# 1.1 树状数组的概念

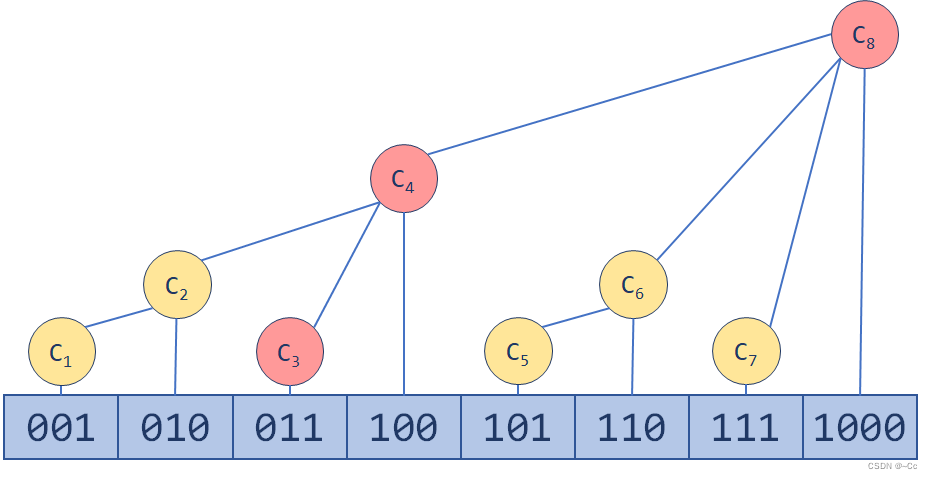
树状数组是一种数据结构，它可以高效地处理区间查询和更新操作。它基于二进制索引树的思想，将一个一维数组表示为一棵完全二叉树。每个节点存储一个值，该值代表其子树中所有元素的某个属性的和或其他聚合函数。

树状数组的主要优点在于，它可以以 O(log n) 的时间复杂度进行区间查询和更新。这使得它在需要频繁处理区间查询和更新的应用中非常有用，例如区间求和、区间最大值查询和区间修改。

# 2. 树状数组的理论基础

### 2.1 树状数组的数学模型

树状数组是一种基于二进制树的数据结构，它将一个一维数组表示为一棵完全二叉树。对于一个长度为 N 的数组，其对应的树状数组的高度为 log2(N)。

树状数组的每个节点存储一个值，该值表示其子树中所有元素的和。通过这种方式，我们可以通过访问树状数组中特定节点来快速计算数组中任意区间元素的和。

### 2.2 树状数组的查询和更新算法

#### 查询算法

给定一个区间 [l, r]，我们可以使用以下算法计算其和：

int query(int l, int r) {
  int sum = 0;
  while (r >= l) {
    if (r % 2 == 0) {
      sum += tree[r];
      r = (r - 2) / 2;
    } else {
      sum += tree[r - 1];
      r--;
    }
  }
  return sum;
}

**参数说明：**

* `l`：区间左端点
* `r`：区间右端点

**代码逻辑分析：**

算法从右端点开始向左遍历，每一步更新和并移动当前位置。如果当前位置为偶数，则将其除以 2 并将和加上该节点的值。否则，将当前位置减 1 并将和加上该节点的值。

#### 更新算法

给定一个索引 `i` 和一个值 `val`，我们可以使用以下算法更新数组中第 `i` 个元素的值：

void update(int i, int val) {
  while (i <= N) {
    tree[i] += val;
    i += (i & -i);
  }
}

**参数说明：**

* `i`：要更新的元素索引
* `val`：要更新的值

**代码逻辑分析：**

算法从索引 `i` 开始向右遍历，每一步更新当前节点的值并移动当前位置。当前位置每次移动 `i & -i` 个单位，该值等于 `i` 的二进制补码。通过这种方式，算法可以高效地更新所有受影响的节点。

# 3. 树状数组的实践应用

### 3.1 树状数组在区间求和中的应用

**问题描述：**

给定一个长度为 n 的数组 A，需要支持以下两种操作：

1. 查询区间 [l, r] 中元素的和。
2. 修改数组 A 中第 i 个元素的值为 x。

**解决方案：**

使用树状数组可以高效地解决该问题。树状数组是一种数据结构，它可以将一维数组转换为一棵二叉树，从而支持快速区间求和和单点修改操作。

**树状数组的构建：**

1. 将数组 A 的元素依次插入到树状数组中。
2. 对于数组 A 中的每个元素 A[i]，将其插入到树状数组的第 i 位。
3. 更新树状数组中第 i 位及其祖先节点的值，以维护区间和。

**查询区间和：**

1. 对于区间 [l, r]，计算其对应的树状数组区间 [L, R]。
2. 查询树状数组中区间 [L, R] 的和。

**修改元素值：**

1. 对于数组 A 中的第 i 个元素，计算其对应的树状数组位置。
2. 更新树状数组中第 i 位及其祖先节点的值，以反映修改后的和。

**代码示例：**

# 创建树状数组
def create_tree(arr):
    tree = [0] * (len