线段树与树状数组：数据结构的高级应用场景

# 1. 线段树与树状数组基础

## 1.1 线段树与树状数组概念引入

线段树（Segment Tree）和树状数组（Binary Indexed Tree，简称BIT），是数据结构中用于存储区间或累加和的高效算法工具。它们在处理诸如区间查询、区间更新等特定问题时，能够提供比基础数组更快的操作时间复杂度。

线段树维护的信息是连续区间的，适用于快速查询、更新区间信息。而树状数组则擅长处理对数时间复杂度内的单点更新和前缀和查询。两者在实现上各有特点，选择合适的工具取决于具体的应用场景。

在本章中，我们将逐步揭开线段树和树状数组的神秘面纱，为后面章节中深入的理论和实现打下坚实的基础。

# 2. 线段树的理论与实现

## 2.1 线段树的概念和结构

### 2.1.1 线段树的定义

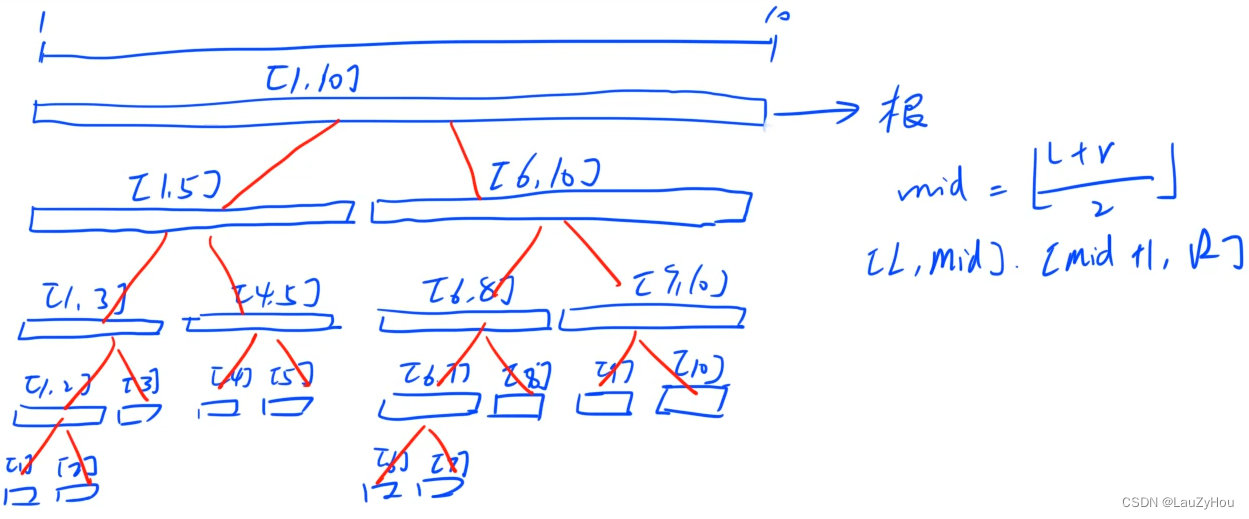
线段树是一种用于存储区间或线段的树形数据结构，它允许快速查询和修改区间内的信息。在计算机科学中，线段树常用于区间查询问题，比如在动态查询一系列区间数据的总和、最大值、最小值、平均值等问题。线段树通常是完全二叉树的形式，每个节点代表一个区间或一个线段，并且父节点表示的区间是子节点表示区间的并集。

### 2.1.2 线段树的特点和优势

线段树的特点在于它能够迅速响应对某一区间内元素的查询和更新操作。与传统的数组操作相比，当处理涉及到区间更新和查询的任务时，线段树能够提供更好的性能。特别是当需要频繁地对数据进行动态修改并且要进行区间查询的时候，线段树的优势就非常明显了。它的空间复杂度是线性的，即为 O(n)，但通过巧妙的设计可以实现对数时间复杂度的操作。

线段树的优势不仅体现在查询和更新的效率上，还在于它的灵活性。通过不同节点的定义，线段树可以适应多种不同的问题场景，如区间求和、区间最值查询等。这些特点使得线段树在如计算几何、数列处理等领域有着广泛的应用。

## 2.2 线段树的操作详解

### 2.2.1 构建线段树

构建线段树是整个线段树操作的基础，通过构建过程可以将一个线性数据结构转换成树形结构以便快速查询和更新区间信息。

struct SegmentTreeNode {
    int start, end; // 节点代表的区间范围
    int sum; // 区间内元素的累加和或其他信息
    SegmentTreeNode *left, *right; // 左右子树指针
};

void buildTree(SegmentTreeNode* root, int start, int end, int* arr) {
    root->start = start;
    root->end = end;
    if (start == end) {
        root->sum = arr[start];
        return;
    }
    int mid = (start + end) / 2;
    root->left = new SegmentTreeNode();
    root->right = new SegmentTreeNode();
    buildTree(root->left, start, mid, arr);
    buildTree(root->right, mid + 1, end, arr);
    root->sum = root->left->sum + root->right->sum; // 合并左右子树的信息
}

以上是一个简单的线段树构建函数示例，其中`SegmentTreeNode`结构体用于表示线段树的节点。构建过程中，递归地将数组`arr`分治到左右子树，并在每个节点中合并左右子树的信息以得到该节点代表区间的信息。

### 2.2.2 区间查询

区间查询是指给定一个区间范围，查询该区间内信息的总和、最大值、最小值等。

int query(SegmentTreeNode* root, int start, int end) {
    if (root->start == start && root->end == end) {
        return root->sum; // 区间匹配，直接返回
    }
    int mid = (root->start + root->end) / 2;
    int sum = 0;
    if (end <= mid) {
        // 查询区间完全在左子树
        sum = query(root->left, start, end);
    } else if (start > mid) {
        // 查询区间完全在右子树
        sum = query(root->right, start, end);
    } else {
        // 查询区间跨越左右子树
        sum = query(root->left, start, mid) + query(root->right, mid + 1, end);
    }
    return sum;
}

该函数递归地查询给定区间的信息，如果区间完全在子树内，则直接查询子树；如果区间跨越两个子树，则分别查询两个子树并合并结果。

### 2.2.3 区间更新

区间更新是指给定一个区间和一个值，将该区间内所有元素更新为该值。

void updateRange(SegmentTreeNode* root, int start, int end, int val) {
    if (root->start == start && root->end == end) {
        root->sum = (end - start + 1) * val; // 区间匹配，更新信息
        return;
    }
    int mid = (root->start + root->end) / 2;
    if (start <= mid) {
        updateRange(root->left, start, end, val);
    }
    if (end > mid) {
        updateRange(root->right, start, end, val);
    }
    root->sum = root->left->sum + root->right->sum; // 合并子树信息
}

该函数递归地更新给定区间内所有元素的值，对于跨越左右子树的区间，分别在两个子树中更新，并在更新后重新合并子树信息。

## 2.3 线段树的算法应用

### 2.3.1 算法时间复杂度分析

线段树的构建过程需要对原始数组中的每个元素进行操作，因此构建线段树的时间复杂度为 O(n)。对于查询和更新操作，由于线段树是高度为 O(log n) 的二叉树，因此在最坏情况下时间复杂度为 O(log n)。

### 2.3.2 实际应用案例分析

实际应用中，线段树常用于处理复杂区间查询和更新问题，例如在实时渲染、音频信号处理等领域。以实时渲染为例，可能需要对一幅图像中连续几个像素的颜色值进行查询或修改，线段树能够高效地完成这一任务。在音频处理中，对连续音频样本值的查询和修改也可以通过线段树来优化。

线段树还常用于解决多维区间查询问题，比如在一个二维平面上进行矩形区域的求和、最值查询等。通过巧妙地将二维问题转化为一维问题，线段树能够灵活应对更复杂的场景。

graph TD
    A[应用案例] --> B[实时渲染]
    A --> C[音频处理]
    A --> D[多维区间查询]

以上mermaid流程图展示了线段树应用案例的多样性，以及它们之间的关联性。通过这种方式，我们可以直观地理解线段树应用的广泛性。

# 3. 树状数组的理论与实现

## 3.1 树状数组的基本原理
### 3.1.1 树状数组的定义

树状数组（Binary Indexed Tree，简称BIT），又称为Fenwick Tree，是一种适用于处理动态数据的二叉树结构，能够高效地处理前缀和、区间和等相关问题。树状数组的特别之处在于其通过巧妙的索引计算，使得其在进行单点修改和求区间和等操作时，都能以对数时间复杂度完成。

树状数组的每个节点都存储着从当前节点的最低一位1开始，到该节点所代表的区间的结束的所有元素的累计和。例如，对于数组中的某个位置 i，它的父节点位置为 `i + (i & -i)`，而子节点的位置则为 `i - (i & -i)`。

### 3.1.2 树状数组的操作

树状数组的操作包括初始化、更新单个值以及查询前缀和。具体实现中，树状数组的构建通常是隐式的，不会直接使用树状结构，而是在一个数组的基础上根据上述索引规则进行操作。

#### 初始化

初始化时，我们通常创建一个与原数组同样大小的数组，所有元素初始化为0。然后在处理更新操作时，按顺序更新每个元素，构建出正确的树状数组。

#### 更新操作

更新操作时，从给定的索引 i 开始，按照树状数组的索引规则，递归向上更新，即更新位置 `i + (i & -i)`、`i + 2*(i & -i)` 直到根节点。每个节点的更新是将给定的新值与原值进行叠加。

#### 区间查询

区间查询时，从给定的右端点 r 开始，按照树状数组的索引规则，递归向下查询，累加沿途所有元素的值，直到左端点 l。此时累加的和即为所求的区间和。

# Python示例代码：树状数组的更新操作和前缀和查询
def update(tree, index, val, n):
    while index <= n:
        tree[index] += val
        index += index & -index

def query(tree, index):
    sum = 0
    while index > 0:
        sum += tree[index]
        index -= index & -index
    return sum

n = len(arr)
tree = [0] * (n + 1)  # 建立树状数组，多出一个位