红黑树深度解析：揭秘其在数据库索引中的革命性作用

# 1. 红黑树的数据结构基础

## 简介
红黑树是一种自平衡的二叉查找树，它在1972年由鲁道夫·贝尔发明。这种数据结构通过在节点中增加一个存储位表示节点的颜色，可以是红或黑。通过这种方式，红黑树确保没有一条路径会比其他路径长出两倍，因而是近似平衡的。

## 基本概念
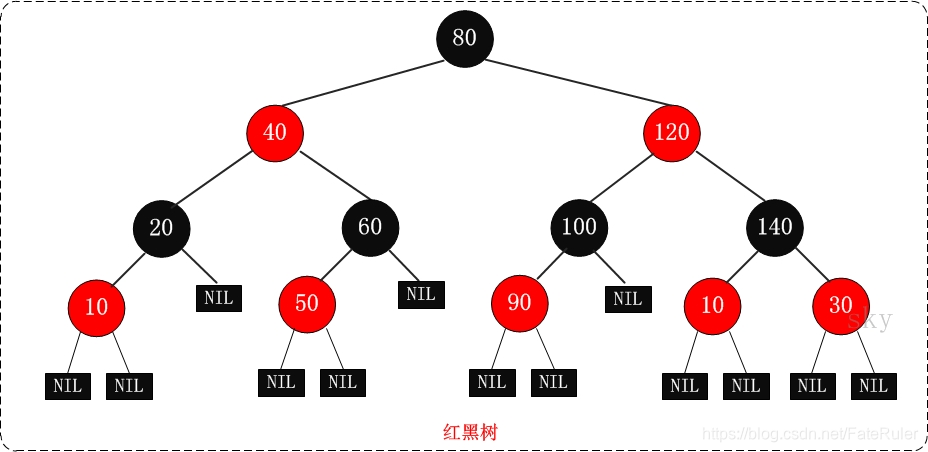
在红黑树中，每个节点遵循以下性质：
- 节点是红色或黑色。
- 根节点是黑色。
- 所有叶子节点（NIL节点，空节点）都是黑色。
- 每个红色节点的两个子节点都是黑色（从每个叶子到根的所有路径上不能有两个连续的红色节点）。
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

通过这些性质，红黑树能够在插入和删除操作后维持其平衡，从而保证最坏情况下操作的时间复杂度为O(log n)。

classDiagram
    class RedBlackTree {
        +Node root
        +Node nil //Sentinel for leaves
        +insert(key)
        +delete(key)
        +balanceTree()
    }
    class Node {
        -int key
        -Node left
        -Node right
        -Node parent
        -boolean isRed
    }

上述类图展示了红黑树主要的类结构和关键方法。红黑树的核心操作包括插入节点、删除节点以及维持树平衡的调整方法。在下一章中，我们将深入探讨红黑树的这些特性及其平衡操作的具体实现细节。

# 2. 红黑树的特性与平衡操作

红黑树是一种自平衡的二叉搜索树，每条路径的长度不会超过其他路径长度的两倍，因此它能在插入、删除操作后保持大致的平衡状态，从而保证查询操作的时间复杂度在最坏情况下仍为 O(log n)。为了达到这种平衡状态，红黑树定义了几个基本性质，并在每次插入或删除节点后通过旋转和重新着色操作来调整树的平衡。

### 2.1 红黑树的五个性质

#### 2.1.1 节点颜色

在红黑树中，每个节点要么是红色，要么是黑色。根节点总是黑色的。这个性质很简单，但它是维持树平衡的基础。

#### 2.1.2 根节点和叶子节点的特性

根节点是黑色的。这一点已经在第一个性质中说明了。此外，红黑树使用的是二叉树的叶子节点，也就是NIL节点，它们都是黑色的。NIL节点是树的外节点，用于表示每个内部节点的叶子边界。

#### 2.1.3 红色节点的子节点必须为黑色

从任意一个节点到其每个叶子节点的所有路径上，不能有两个连续的红色节点。这个性质确保了没有一条路径比其他路径长出两倍，从而避免了树退化为链表。

### 2.2 红黑树的插入操作

#### 2.2.1 标准插入过程

插入节点的时候，这个节点首先被涂成红色。然后，它被插入到树中适当的位置，就如同在普通的二叉搜索树中一样。因为添加的节点是红色的，所以这个操作不会违反性质2（根节点和叶子节点的特性）。但是，可能会违反性质3（红色节点的子节点必须为黑色），所以我们需要进行调整。

#### 2.2.2 插入后颜色调整和树的平衡

插入节点后，可能会需要进行一系列的旋转和重新着色操作，以保证树的平衡。插入操作后可能会违反的两个性质是：性质3和性质4（从任一节点到其每个叶子节点的所有简单路径都包含相同数目的黑色节点）。通过递归地重新着色和旋转（左旋或右旋），可以修复这些违反的性质。

// 伪代码示例，表示红黑树节点的插入操作后进行颜色调整的过程
function insertAdjust(node) {
    // 如果插入节点的父节点是黑色，则不需要调整
    if (node.parent == null || node.parent.color == BLACK) {
        return;
    }

    // 如果插入节点的父节点和叔叔节点都是红色
    if (node.parent.color == RED &&叔叔节点(node) != null &&叔叔节点(node).color == RED) {
        // 将父节点和叔叔节点涂黑
        node.parent.color = BLACK;
        叔叔节点(node).color = BLACK;
        // 将祖父节点涂红
        祖父节点(node).color = RED;
        // 递归调整祖父节点
        insertAdjust(祖父节点(node));
        return;
    }

    // ... 更多插入调整的逻辑代码
}

### 2.3 红黑树的删除操作

#### 2.3.1 标准删除过程

删除节点时，如果被删除的节点有两个子节点，那么我们用其右子树中的最小节点（或左子树中的最大节点）来替换它，然后删除那个最小节点。如果要删除的节点只有一个子节点或者没有子节点，直接删除这个节点即可。

#### 2.3.2 删除后颜色调整和树的平衡

删除节点可能会导致树的某些性质被违反，尤其是性质3和性质4。为了修复这些性质，可能需要进行节点的重新着色和树的旋转操作。删除一个黑色节点可能会导致从某些叶子节点到根节点的路径上的黑色节点数量减少，这需要通过旋转和重新着色来恢复平衡。

// 伪代码示例，表示红黑树节点的删除操作后进行颜色调整的过程
function deleteAdjust(node) {
    // ... 删除节点的调整逻辑，确保树平衡
}

红黑树的平衡操作是理解这棵树的关键，而对这些操作的深入分析和理解将帮助我们在需要实现和优化红黑树时，更好地处理各种复杂情况。

# 3. 红黑树在数据库索引中的应用

## 3.1 索引与数据检索效率
### 3.1.1 索引的基本概念和作用
索引是数据库中一项重要的数据结构，它能够大幅提高数据检索的效率。在没有索引的情况下，数据库在检索数据时通常需要进行全表扫描，即顺序读取每一行数据来匹配查询条件，这在数据量较大时显得异常低效。而索引则为数据库表中一列或多列提供了快速检索的路径。

索引的工作原理类似于书籍的目录，通过索引，数据库管理系统可以直接定位到包含特定值的数据行，而无需逐行扫描整个表。这样，数据库的查询性能得到显著提升，尤其是在执行查询和连接操作时。

### 3.1.2 索引的数据结构选择
为了实现索引，数据库系统通常会选用一种高效的数据结构，比如B树、B+树、哈希表或是红黑树。在这些数据结构中，红黑树因其平衡性能而被广泛用于数据库索引。红黑树的平衡操作保证了数据的有序性，同时将查找、插入、删除操作的时间复杂度都维持在O(log n)的水平。

相比于其他结构，如B树和B+树，红黑树在节点插入和删除时能提供更好的性能保障，因为它不需要像B树那样频繁地进行节点分裂和合并。这些特性使得红黑树在索引小型或中型数据库时非常有效。

## 3.2 红黑树作为索引的实现原理
### 3.2.1 红黑树索引的构建过程
红黑树索引的构建过程包括创建索引结构、插入索引节点以及维护索引平衡。

1. 创建索引结构：根据索引键值和数据记录之间的对应关系，初始化一棵空的红黑树。
2. 插入索引节点：当数据库表中插入新的数据行时，相应的键值会作为索引节点插入到红黑树中。红黑树通过特定的规则维护其平衡，例如在插入新节点后可能会触发颜色翻转或树旋转。
3. 维护索引平衡：红黑树通过颜色调整和树旋转来保持平衡，确保树高维持在对数级别，从而保证了索引操作的效率。

### 3.2.2 红黑树索引的优势分析
红黑树作为数据库索引的优势在于其平衡性。红黑树的平衡机制减少了在最坏情况下的查询时间复杂度，使得其在动态变化的数据集中的表现非常稳定。它保证了数据检索的高效性，即使在数据集大小经常发生变化的情况下也能提供可预测的性能。

同时，红黑树索引相比其他类型的索引，例如哈希表，能够支持范围查询。哈希表在处理范围查询时需要扫描整个表，而红黑树索引可以在O(log n + m)的时间复杂度内完成，其中m是查询返回的数据行数。

## 3.3 红黑树索引在数据库中的性能评估
### 3.3.1 索引维护的成本
虽然红黑树索引带来了高效的查询性能，但维护索引的成本也不容忽视。索引的维护涉及到节点插入、删除、更新等操作。在每次操作后，红黑树可能需要进行多次颜色调整和树旋转来恢复平衡状态。这些操作虽然复杂度为O(log n)，但在数据更新频繁的情况下会增加数据库的负担。

### 3.3.2 数据操作的时间复杂度
在进行数据插入和删除操作时，红黑树索引的时间复杂度均为O(log n)。查找操作通常更快，因为其时间复杂度仅为O(log n)。然而，这并不意味着所有的数据库操作都应当使用索引。为了获得最佳性能，数据库管理员需要在查询速度和索引维护成本之间找到平衡点。

例如，对于经常进行更新操作的表，可能会选择创建部分索引或者不创建索引，以此减少更新操作的开销。而在读操作远多于写操作的场景中，红黑树索引则能提供较大的性能优势。

下面是红黑树索引实现原理的代码示例，使用Python语言演示构建红黑树节点和插入操作：

class Node:
    def __init__(self, data, color="red"):
        self.data = data
        self.color = color
        self.parent = None
        self.left = None
        self.right = None

class RedBlackTree:
    def __init__(self):
        self.NIL = Node(None, "black")  # 使用NIL节点表示空节点，标记为黑色
        self.root = self.NIL

    def insert(self, data):
        new_node = Node(data)
        new_node.left = self.NIL
        new_node.right = self.NIL
        parent = None
        current = self.root

        # 标准二叉搜索树的插入过程
        while current != self.NIL:
            parent = current
            if new_node.data < current.data:
                current = current.left
            else:
                current = current.right

        new_node.parent = parent
        if parent is None:
            self.root = new_node
        elif new_node.data < parent.data:
            parent.left = new_node
        else:
            parent.right = new_node

        # 插入后颜色调整和树的平衡（需要实现红黑树的平衡机制）
        # ...
        pass

# 示例：创建红黑树并插入节点
rbt = RedBlackTree()
rbt.insert(10)
rbt.insert(20)
rbt.insert(30)

在上述代码中，我们定义了一个红黑树的节点类 `Node` 和红黑树类 `RedBlackTree`。`Node` 类包含数据值、颜色、父节点、左右子节点等属性。`RedBlackTree` 类则包含了根节点、插入节点的逻辑和需要进一步实现的红黑树平衡调整逻辑。

请注意，完整的红黑树实现包括多种情况的调整规则，比如左旋、右旋和颜色翻转等，由于篇幅限制，这里没有详细展示。

在使用红黑树作为数据库索引时，需要在数据库系统中实现相应的索引管理机制。构建索引的过程和维护成本直接影响数据库性能和存储空间的使用。因此，了解红黑树索引的基本原理和实现是数据库开发者和维护者的重要技能。

以上内容对红黑树在数据库索引中的应用进行了全面的介绍。下一章节将继续探讨红黑树的高级应用与优化。

# 4. 红黑树的高级应用与优化

红黑树不仅在理论计算机科学中占有重要地位，它还在现代软件开发中有着广泛的应用。从数据库索引到文件系统，再到其他需要高效数据结构的领域，红黑树的特性让它成为了诸多算法实现的核心。

## 4.1 扩展红黑树结构

### 4.1.1 2-3-4树与红黑树的关系

2-3-4树是一种多路平衡查找树，每个多路节点可包含两个、三个或四个子节点。有趣的是，2-3-4树与红黑树之间存在着一种等价关系。在2-3-4树中，如果把拥有两个子节点的视为黑节点，拥有三个子节点的视为红色节点，拥有四个子节点的视为红色节点后再添加一个黑色节点，那么所得到的树形结构就会符合红黑树的五个性质。

在实现上，2-3-4树的插入和删除操作可以通过一系列的颜色调整和旋转操作转换为红黑树的等价操作。例如，2-3-4树中的拆分3节点或4节点操作，可以对应到红黑树中的颜色翻转和两次旋转操作。

flowchart TD
    A[2-3-4树节点] -->|映射| B[红黑树节点]
    A1[2节点] -->|对应| B1[黑节点]
    A2[3节点] -->|对应| B2[红节点]
    A3[4节点] -->|对应| B3[红节点+黑节点]

### 4.1.2 B树与红黑树的比较

B树（B-Tree）是一种广泛应用在数据库和文件系统的多路平衡查找树。与红黑树相比，B树更适合磁盘等块设备的操作，因为它在多路分裂时可以减少I/O操作次数。然而，红黑树在内存中的表现往往更好，因为它能够更好地保持平衡状态。

虽然两者有不同，但它们在许多操作上有着相似的算法复杂度。例如，B树的插入和删除操作都依赖于节点分裂和合并的策略，这与红黑树的平衡调整类似。在实际应用中，选择哪一种数据结构往往取决于应用场景和具体需求。

## 4.2 红黑树在现代数据库的优化

### 4.2.1 并发控制和锁策略

红黑树作为数据库索引结构时，其性能在并发环境下尤为重要。为了减少锁的争用，现代数据库通常会采用乐观锁或悲观锁策略。乐观锁策略允许读操作不加锁，而写操作在提交前检查是否有冲突。悲观锁策略则是在读写操作时加锁，确保数据的一致性。

例如，MySQL的InnoDB存储引擎在使用红黑树作为索引时，对于乐观并发控制采用了MVCC（多版本并发控制）机制，而悲观锁则表现为对索引节点的锁定。这样设计使得红黑树在多用户环境下依然能维持高效的性能表现。

### 4.2.2 物理存储和数据页结构

在物理存储方面，红黑树节点常常映射到数据页中。数据页是存储系统中最小的I/O单位。红黑树的节点分裂和合并操作会影响到数据页的分配和回收。

大多数数据库管理系统会将数据页设计为固定大小，并在页内实现红黑树结构。这样的设计可以有效减少由于节点分裂导致的频繁I/O操作，提高效率。

## 4.3 红黑树的实际案例分析

### 4.3.1 开源数据库中的红黑树应用

例如，SQLite数据库系统中的索引结构就使用了红黑树。SQLite通过红黑树来快速定位和排序记录，从而加快查询速度。SQLite通过精心设计的内存管理和磁盘I/O策略，使得红黑树的性能在资源受限的环境中得到了优化。

### 4.3.2 商用数据库中的红黑树应用

在商用数据库如Oracle中，红黑树也被用作索引结构。Oracle数据库在处理大量并发事务时，通过红黑树的高效平衡操作，保证了数据库索引的性能。Oracle还采用了分区技术，在大型数据库中通过红黑树优化分区索引，进一步提高了查询效率。

在实际案例中，我们看到红黑树在各种数据库实现中的优化方法和应用策略，显示了它作为索引结构在数据管理上的灵活性和强大性能。

在下一章节中，我们将深入探讨红黑树的未来展望，包括它在新兴技术中的角色和新型索引结构的发展趋势。

# 5. 红黑树的未来展望

随着技术的不断进步，数据库索引技术也在不断地演进。红黑树作为一种成熟且广泛应用于数据库索引的数据结构，它的未来展望同样备受关注。本章将对红黑树在数据库索引技术中的发展趋势进行深入探讨，并分析其在新兴技术中的潜在角色。

## 5.1 数据库索引技术的发展趋势

### 5.1.1 新型索引结构的探索

随着大数据和云计算技术的发展，传统数据索引结构面临着新的挑战和机遇。新型索引结构的探索方向主要集中在提高索引的可扩展性、优化空间利用率以及支持更复杂的数据查询需求。

例如，LSM树（Log-Structured Merge-Tree）是一种新型索引结构，它通过日志结构合并树的存储方式，优化了写操作的性能，特别适合于写密集型的存储系统。相比之下，红黑树虽然在插入和删除操作上保证了较高的效率，但在大规模数据量的情况下，其性能可能会受到树高增长的影响。

为了优化空间利用率，倒排索引（Inverted Index）常用于全文搜索，它通过存储关键字到文档的映射关系，能够高效地支持文本查询。未来，我们可能会看到红黑树与这些新型索引结构的融合，形成混合索引模型，以利用各自的优势。

### 5.1.2 分布式数据库中的索引策略

随着分布式数据库的普及，索引策略也需要适应分布式环境的特性。在分布式系统中，数据需要被切分成多个分片，分布在不同的节点上。这意味着索引也需要进行水平切分，以便于跨节点的查询和操作。

红黑树在分布式环境下的应用可能会采用分片技术，将树结构分别维护在不同的节点上，并通过分布式事务和一致性协议来保证全局的一致性。此外，分布式环境下索引的更新和查询性能将更加依赖于网络延迟和节点间通信的效率。

## 5.2 红黑树在新兴技术中的角色

### 5.2.1 数据库缓存机制的集成

缓存是数据库性能优化中的一项关键技术，它能够显著减少对磁盘I/O的需求。在缓存机制中，红黑树可以用来实现内存中的索引结构，以加快数据检索速度。当缓存失效时，可以利用红黑树的高效插入和删除特性，快速地将数据从磁盘迁移到内存中。

### 5.2.2 红黑树与机器学习的交叉研究

随着人工智能技术的崛起，机器学习算法在数据库管理中的应用逐渐增多。红黑树作为一种有序的数据结构，可以被用来优化机器学习中的某些算法，特别是在处理具有序关系特征的数据时。

例如，在决策树算法中，红黑树可以被用作计算信息增益的辅助数据结构，以加速数据集的划分过程。红黑树的特性能够帮助算法更高效地处理大量的分类数据，提高机器学习模型训练的速度和效果。

在结束第五章的讨论之前，我们可以预见，红黑树在未来的数据库索引技术以及新兴技术中，将继续扮演重要角色。无论是在探索新的索引结构，还是在分布式数据库的优化，或是与机器学习的交叉应用中，红黑树都会以它独特的优势，为技术的进步做出贡献。