哈夫曼树：揭秘数据压缩背后的树算法原理

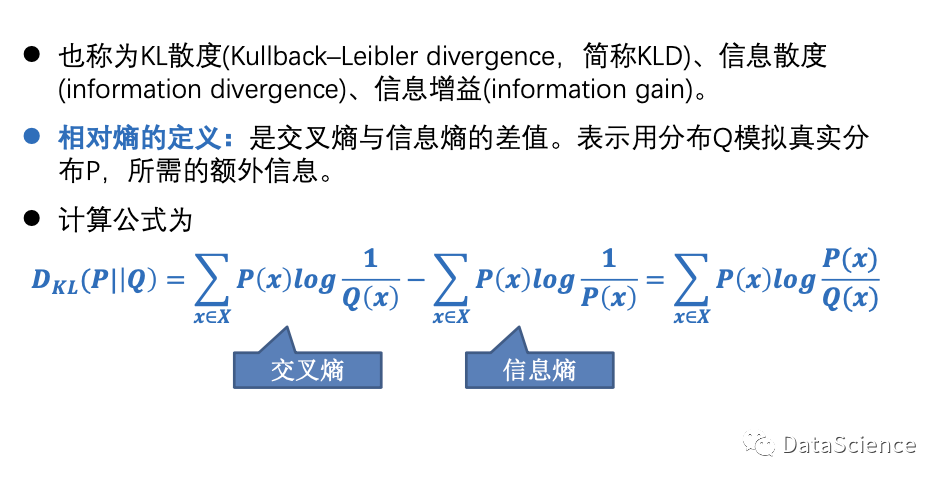
# 1. 哈夫曼树的基本概念与原理

哈夫曼树（Huffman Tree），又称最优二叉树，是一种带权路径长度最短的二叉树，广泛应用于数据压缩领域。在哈夫曼树中，权值较小的节点会出现在树的下层，而权值较大的节点则位于上层。这种构造方式使得整棵树的加权路径长度达到最小。

构建哈夫曼树的过程基于贪心算法的思想，按照权值大小选择节点进行合并。每个节点的权值通常表示在数据压缩中，该节点所代表字符出现的频率。字符出现频率越高，其代表的节点在树中的位置越靠近根节点，从而使得高频字符在编码时使用较短的二进制代码。

哈夫曼树的优势在于通过有效的数据表示方法，实现数据的有效压缩。在不同的应用场景中，哈夫曼编码可以大幅度减少存储空间需求，并提高数据传输效率，尤其是在需要快速数据访问和处理的场合，如多媒体数据压缩、网络数据传输等领域。接下来章节我们将深入探讨哈夫曼树的构建过程，以及它在数据压缩中的应用。

# 2. 哈夫曼树的构建过程

哈夫曼树，又称为最优二叉树，是一种带权路径长度最短的二叉树。它的构建过程涉及一系列复杂算法，并且通过分析信息熵和实现信息编码，来达到压缩数据的目的。下面将详细介绍这一过程，从熵的概念开始，逐步展示如何构建出一个完整的哈夫曼树。

### 2.1 熵的概念与信息量的计算

#### 2.1.1 熵的基本定义

熵是信息论中的一个核心概念，它用来度量一个信息源的不确定性。在数学上，熵是随机变量不确定性的度量。对于一个离散随机变量X，其熵定义为：

\[ H(X) = - \sum_{i=1}^{n} p(x_i) \log_2 p(x_i) \]

这里的 \( p(x_i) \) 表示随机变量X取第i个值的概率。熵越大，信息的不确定性越高。理解熵，有助于我们量化信息的平均信息量，并为后续哈夫曼编码的构建提供理论基础。

#### 2.1.2 信息量的计算方法

信息量是衡量单个事件发生时所带来的信息的多少。对于一个随机事件，其信息量计算公式为：

\[ I(x_i) = - \log_2 p(x_i) \]

这表示具有高概率发生的事件的信息量小，而低概率发生的事件具有较大的信息量。通过计算每个事件的信息量，我们可以构建信息量的集合，该集合是实现哈夫曼编码的基础。

### 2.2 哈夫曼编码的构建步骤

#### 2.2.1 权重的分配与节点的创建

哈夫曼编码的构建开始于为各个信息源分配权重。这些权重通常代表了信息出现的概率或频率。在构建树之前，我们需要为每个符号创建一个树节点，并根据权重初始化它们。

假设我们有这样一组数据：

| 符号 | 权重 |
| :---: | :--: |
| a | 0.4 |
| b | 0.2 |
| c | 0.1 |
| d | 0.3 |

我们可以创建相应的节点：

a (权重: 0.4)
b (权重: 0.2)
c (权重: 0.1)
d (权重: 0.3)

#### 2.2.2 树的生长与合并策略

创建完节点后，我们按照哈夫曼算法的合并策略，选取两个最小权重的节点合并为一个新节点，这个新节点的权重是两个子节点权重之和。重复这个合并过程，直到所有的节点都被合并成一棵树。

以示例中的节点为例，首先合并权重最小的 `c` 和 `d`：

合并后节点 cd (权重: 0.4)
a (权重: 0.4)
b (权重: 0.2)

继续合并 `b` 和 `cd`：

合并后节点 bcd (权重: 0.6)
a (权重: 0.4)

最后合并 `a` 和 `bcd` 得到完整的哈夫曼树：

          *
         / \
        /   \
       /     \
     a(0.4)   bcd(0.6)
              /    \
             /      \
           cd(0.4)  b(0.2)
           /   \
         c(0.1) d(0.3)

#### 2.2.3 完整哈夫曼树的形成

通过上述步骤，我们完成了哈夫曼树的构建。这棵哈夫曼树能够确保权重大（出现频率高）的节点有较短的路径长度，而权重小的节点路径长度较长。这种结构确保了编码的效率，使得整体的平均编码长度最小。

### 2.3 算法效率分析

#### 2.3.1 时间复杂度

哈夫曼树的构建过程涉及排序和选择最小权重节点的步骤。在最坏的情况下，每次合并后需要重新排序，这会导致时间复杂度较高。然而，如果使用优先队列（比如最小堆）来存储节点，可以保证每次合并操作的时间复杂度为O(logn)，其中n是节点的总数。由于构建过程中合并次数为n-1，所以整个构建过程的时间复杂度为O(nlogn)。

#### 2.3.2 空间复杂度

哈夫曼树的构建需要存储每个节点及其权重，以及每个节点的父节点信息。假设所有的节点都是通过n次合并得到的，那么存储所有节点的信息需要的空间复杂度是O(n)。除此之外，我们需要额外的空间来存储优先队列，其空间复杂度也是O(n)。因此，哈夫曼树构建的总空间复杂度为O(n)。

哈夫曼编码通过信息熵的计算和树的构建过程，实现了高效的数据编码，使我们能够在不丢失信息的前提下，有效减少数据的存储空间。接下来，我们将探讨哈夫曼编码在实际中的应用，以及如何通过压缩和解压缩来优化数据的存储和传输效率。

# 3. 哈夫曼树在数据压缩中的应用

## 3.1 数据压缩的理论基础

### 3.1.1 无损压缩与有损压缩

数据压缩技术根据压缩过程中是否保留原始数据，可以分为无损压缩和有损压缩。无损压缩保证数据在压缩和解压过程中完全一致，即原始数据的每个比特位都被无误地保存下来。无损压缩广泛应用于文本文件、程序代码和某些类型的图像文件中，如PNG和GIF格式的图像。

有损压缩则允许在压缩过程中舍弃一些非关键信息，从而达到更高的压缩比。这意味着原始数据在被重建时会有一定的信息损失，但通常这种损失对于人类感觉系统来说是不可察觉的，因此它在多媒体数据如音频、视频以及高分辨率图像中得到了广泛应用。

### 3.1.2 哈夫曼压缩与其他压缩技术比较

哈夫曼压缩作为一种无损压缩技术，其主要优势在于压缩比通常比传统编码方法更高，尤其是当待压缩数据中字符出现频率差