二叉搜索树构建艺术：平衡技巧与实战案例

# 1. 二叉搜索树概述与特性

在计算机科学和数据结构领域中，二叉搜索树（BST）是一种被广泛使用的数据结构，它支撑着如数据库索引、文件系统目录管理和其他需要高效查找、插入和删除操作的应用。BST有其独特的特性，它不仅存储键值对，还通过一种特定的方式来组织数据，使得能够快速地在树中进行查找和排序操作。

## 1.1 二叉搜索树的基本概念

二叉搜索树是二叉树的一种，其中每个节点都包含一个键值对。树中的每个节点都可以有两个子节点，称为左子节点和右子节点。BST的关键特性是：

- **左子树上的所有节点的键值都小于其根节点的键值**。
- **右子树上的所有节点的键值都大于其根节点的键值**。
- **左右子树也分别为二叉搜索树**。

这个简单的规则定义了一个有序的树结构，这使得搜索操作可以通过递归或迭代的方式高效完成。这种属性为二叉搜索树带来了对数时间复杂度的查找效率，但若树高度失衡，可能导致性能退化到线性时间复杂度。

## 1.2 二叉搜索树的特性

- **有序性**：二叉搜索树按照键值有序排列，这意味着中序遍历可以产生有序的键值序列。
- **动态维护性**：二叉搜索树能够快速地插入新节点或删除节点，并维持其搜索效率。
- **查找效率**：在理想情况下，二叉搜索树的高度与元素数量的对数成正比，即O(log n)，这保证了搜索、插入和删除操作的效率。

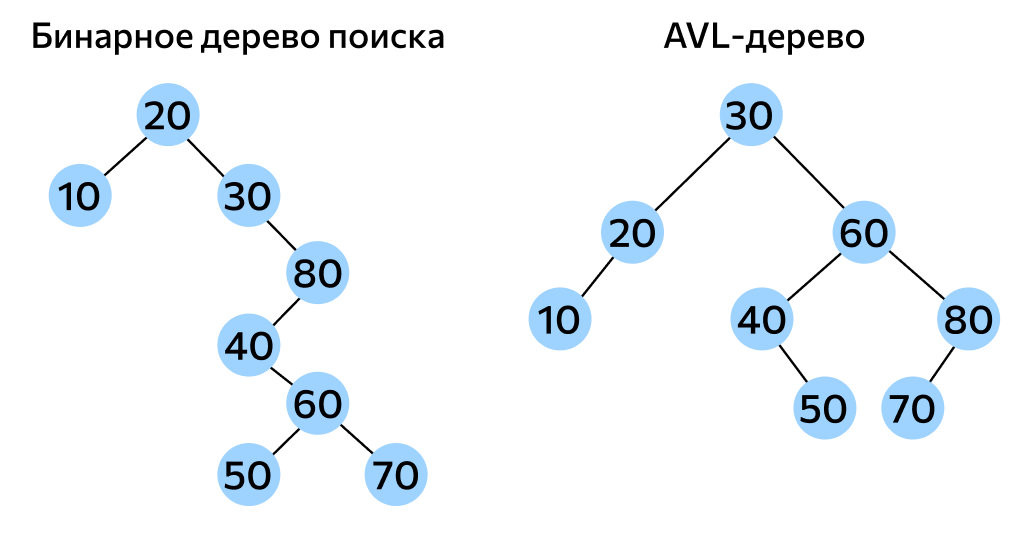
然而，二叉搜索树的性能高度依赖于树的形状。理想情况下，二叉搜索树是高度平衡的，但这种平衡状态很难自然保持。因此，在实际应用中，人们经常采用平衡二叉搜索树的变种，如AVL树和红黑树，这些变种通过调整树的结构来保持平衡，进而保持操作的高效率。

以上是对二叉搜索树的概述和基本特性的介绍，接下来的章节将深入探讨平衡二叉搜索树的原理，以及它们如何保证操作的高效率。

# 2. 理解平衡二叉搜索树的原理

## 2.1 平衡二叉树的基本概念

### 2.1.1 二叉搜索树的定义

二叉搜索树（Binary Search Tree, BST）是一种特殊的二叉树，其性质保证了树中任何节点的左子树只包含小于当前节点的数，而右子树只包含大于当前节点的数。这种特性使得二叉搜索树可以高效地进行查找、插入和删除操作，最坏情况下，时间复杂度为O(n)，但平均情况下为O(log n)。

二叉搜索树的设计目标是保持数据有序，以便快速地检索。为了维持这种特性，二叉搜索树在插入和删除节点时，可能需要通过树的旋转操作来重新平衡树结构。

### 2.1.2 平衡因子与平衡条件

在平衡二叉树中，每个节点的左右子树的高度差称为平衡因子（Balance Factor, BF）。为了保持树的平衡，通常要求每个节点的平衡因子的绝对值不超过1，即BF的值为-1、0或1。

平衡二叉树通常指的是任何节点的左右子树高度差不超过1的二叉搜索树。例如，AVL树和红黑树都是平衡二叉搜索树的典型实现。它们通过不同的旋转策略来维持树的平衡，从而保证树的插入、删除和查找操作具有较高的效率。

## 2.2 AVL树的平衡策略

### 2.2.1 AVL树的旋转操作

AVL树是一种高度平衡的二叉搜索树，它通过在节点插入和删除后进行旋转操作来维持平衡。AVL树的旋转分为四种基本类型：单右旋转（RR）、单左旋转（LL）、左右双旋转（LR）和右左双旋转（RL）。

- **单右旋转（RR）**：当一个节点的平衡因子从0变为+2，并且其右子树的平衡因子为+1时，需要进行单右旋转。这种旋转会将右子树的根节点作为新树的根，原节点成为新根的左子节点。
- **单左旋转（LL）**：与单右旋转相反，当一个节点的平衡因子从0变为-2，并且其左子树的平衡因子为-1时，进行单左旋转。
- **左右双旋转（LR）**：当一个节点的平衡因子从0变为+2，并且其右子树的平衡因子为-1时，需要先对右子树进行左旋转，然后再进行单右旋转。
- **右左双旋转（RL）**：当一个节点的平衡因子从0变为-2，并且其左子树的平衡因子为+1时，需要先对左子树进行右旋转，然后再进行单左旋转。

### 2.2.2 AVL树的插入与删除平衡

在AVL树中，每次插入或删除节点后，都要检查每个节点的平衡因子。一旦发现节点的平衡因子的绝对值超过1，就需要进行相应的旋转操作来重新平衡树。

- **插入操作后的平衡**：插入节点时，从插入点开始沿着父节点回溯到根节点，逐个检查并调整每个节点的平衡。如果节点的平衡因子发生变化，则根据上述四种旋转操作之一进行调整。
- **删除操作后的平衡**：删除节点可能引起更复杂的平衡问题，因为可能会移除平衡因子为0的节点。在删除节点后，需要从被删除节点的父节点开始，沿着路径向上检查每个节点，进行必要的旋转操作。

## 2.3 红黑树的平衡策略

### 2.3.1 红黑树的性质

红黑树是一种自平衡的二叉搜索树，它在每个节点上增加了一个存储位来表示节点的颜色，可以是红（RED）或黑（BLACK）。红黑树的性质确保了没有任何一条路径会比其他路径长出两倍，因而是近似平衡的。

红黑树的五个基本性质如下：
1. 每个节点要么是红的，要么是黑的。
2. 根节点是黑的。
3. 每个叶子节点（NIL节点，空节点）是黑的。
4. 如果一个节点是红的，那么它的两个子节点都是黑的。
5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

### 2.3.2 红黑树的调整操作

在红黑树中插入或删除节点后，可能会违反上述性质，特别是性质4和5。因此，红黑树定义了一系列的调整操作来重新平衡树：

- **颜色变换（Color Flip）**：改变一个节点及其子节点的颜色。
- **左旋转（Left Rotation）**：将某个节点的右子节点提升为父节点，并将原节点变成新父节点的左子节点。
- **右旋转（Right Rotation）**：与左旋转相对应的操作。

调整操作包括：
1. 插入调整：插入节点后，可能需要进行颜色变换和旋转操作来重新满足红黑树的性质。
2. 删除调整：删除节点可能会导致某些路径上的黑色节点减少，需要通过颜色变换和旋转操作来重新平衡树。

红黑树与AVL树相比，插入和删除操作的旋转次数通常较少，因此在大量插入和删除操作的场景下，红黑树有较好的性能表现。而AVL树在需要频繁查找操作的场景下更加高效。

以上章节内容详细介绍了平衡二叉搜索树（AVL树和红黑树）的基本概念和平衡策略。平衡二叉搜索树通过特定的树旋转操作和平衡维持机制，确保了数据结构在插入、删除和查找操作中的效率。下一章节将深入探讨这些平衡二叉搜索树的代码实现细节。

# 3. 平衡二叉搜索树的实现细节