二叉树层序遍历指南：广度优先搜索的实用技巧

# 1. 二叉树层序遍历的原理与应用

二叉树是计算机科学中的一个基本数据结构，它在逻辑上呈现出一种分支结构。二叉树的层序遍历是按照树的层次从上到下、从左到右的顺序访问所有节点的过程。尽管二叉树的概念看似简单，但其层序遍历的应用却十分广泛，它为许多复杂的算法问题提供了解决的基础，尤其是在需要按层次顺序处理数据时。

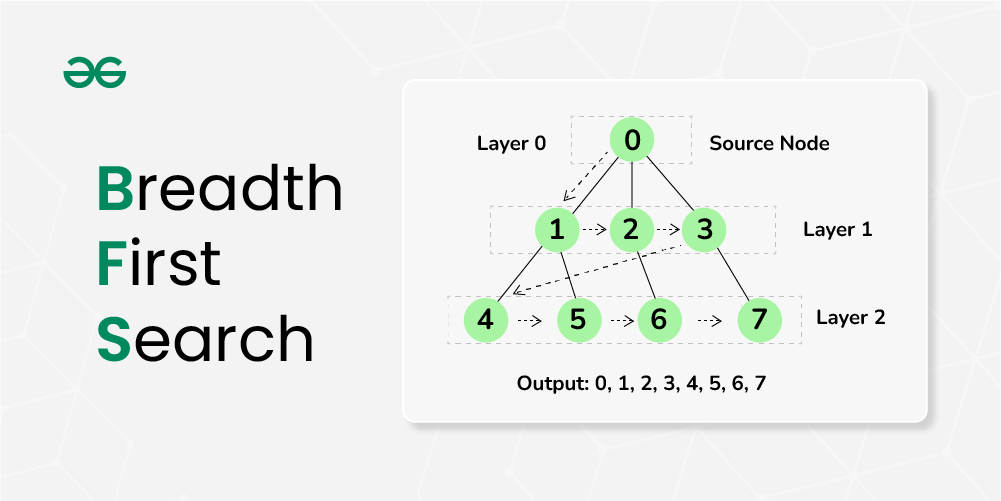
层序遍历的原理基于广度优先搜索（BFS），它使用队列这一数据结构来保证访问顺序。算法开始时，首先将根节点加入队列。之后，每当队列不为空，就从队列中取出一个节点，并将该节点的子节点按照从左到右的顺序加入队列。这一过程重复进行，直到队列为空，即所有节点都被访问过。

在实际应用中，层序遍历可用于构建层级索引、实现按层次的数据处理以及在图形用户界面（GUI）中以分层方式展示数据等场景。通过层序遍历，我们能够更有效地分析和理解树形数据的结构，从而在不同的业务逻辑中发挥其特有的优势。

# 2. 二叉树层序遍历的理论基础

## 2.1 二叉树的概念及其结构特点

### 2.1.1 二叉树的定义和类型

二叉树是每个节点最多有两个子节点的树形数据结构，通常子节点被称作“左子节点”和“右子节点”。在计算机科学中，二叉树被广泛用于构建搜索树、排序算法、以及各种数据表达和处理的结构。根据节点的特性，二叉树又可以细分为以下类型：

- 完全二叉树：除了最后一层外，每一层都被完全填满，且所有节点都向左对齐。
- 满二叉树：每一层的节点数都达到最大值，即层序遍历时，每层的节点数目都符合二的幂次。
- 平衡二叉树（AVL树）：任意节点的两个子树的高度差不超过1。
- 二叉搜索树（BST）：对于树中的每个节点，其左子树上所有节点的值都小于它，其右子树上所有节点的值都大于它。
- 哈夫曼树（Huffman Tree）：带权路径长度最短的二叉树，常见于数据压缩算法中。

### 2.1.2 二叉树的性质和应用场景

二叉树的性质是层序遍历等算法设计的基础。例如，一个完全二叉树的第i个节点的左子节点索引是 `2*i`，右子节点索引是 `2*i + 1`。同时，对于任何节点，其深度等于其父节点索引的对数（以2为底）。这些性质在实现层序遍历时尤为重要，因为它们有助于有效地访问和处理节点。

二叉树在很多领域都有其实际应用：

- 数据库索引：二叉搜索树被用作数据库索引，提供快速的数据检索能力。
- 表达式解析：在编译原理中，二叉树用于表示数学表达式和语法结构。
- 排序算法：比如快速排序和归并排序，可以利用二叉树的性质快速排序。
- 人工智能：决策树是人工智能中用于分类和决策的一种算法，它的核心是一个二叉树。

## 2.2 层序遍历的算法原理

### 2.2.1 广度优先搜索（BFS）简介

广度优先搜索（Breadth-First Search, BFS）是一种用于图的遍历或者树的层序遍历算法。它从一个节点开始，逐层遍历图的所有邻近节点，直到找到所需的节点或者遍历完所有节点。在二叉树层序遍历中，通常使用队列来实现BFS。算法开始时，首先将根节点入队；当队列非空时，节点出队，并将其左右子节点分别入队。这一过程不断重复，直到所有节点都被访问。

### 2.2.2 层序遍历算法的步骤和效率

层序遍历算法的步骤可以分为以下几个主要部分：

1. 创建一个空队列。
2. 将根节点入队。
3. 当队列非空时，执行以下步骤：
a. 节点出队。
b. 访问该节点（例如，输出节点的值）。
c. 如果该节点有左子节点，将左子节点入队。
d. 如果该节点有右子节点，将右子节点入队。
4. 重复步骤3，直到队列为空。

算法的时间复杂度和空间复杂度均为O(n)，其中n是树中节点的数量。这是因为在最坏情况下，每个节点都会入队一次且仅一次。

接下来，我们将深入探讨层序遍历的代码实践，包括基础实现和优化技巧。我们会从最简单的队列实现开始，逐步深入到实际项目案例，展示层序遍历在不同场景下的应用。

# 3. 实现二叉树层序遍历的代码实践

## 3.1 基础的层序遍历实现

### 3.1.1 使用队列进行层序遍历

层序遍历是二叉树遍历的一种，按照树的层次从上到下、从左到右的顺序访问所有节点。在代码实现上，队列是层序遍历的核心数据结构。下面是一个基于队列实现的二叉树层序遍历的Python代码示例：

from collections import deque

class TreeNode:
    def __init__(self, value=0, left=None, right=None):
        self.val = value
        self.left = left
        self.right = right

def levelOrder(root):
    if not root:
        return []

    result = []
    queue = deque([root])
    while queue:
        level_size = len(queue)
        current_level = []
        for _ in range(level_size):
            node = queue.popleft()
            current_level.append(node.val)
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)
        result.append(current_level)
    return result

### 3.1.2 层序遍历的结果输出和分析

执行上述代码，以一个示例树为例：

    1
   / \
  2   3
 / \   \
4   5   6

执行`levelOrder(root)`将返回：

[[1], [2, 3], [4, 5, 6]]

每个子列表表示树的一层，从上到下依次为根节点层、左子树和右子树层，从而实现了层序遍历。层序遍历输出的数组顺序直观地反映了树的层次结构。

## 3.2 层序遍历的优化技巧

##