字典树与AC自动机：高效字符串匹配解决方案

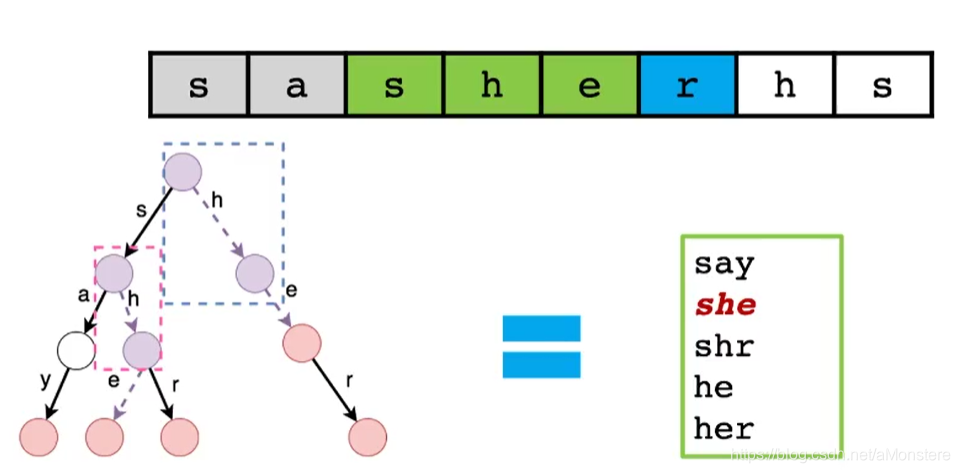
# 1. 字典树与AC自动机简介**

字典树和AC自动机是两种重要的数据结构，广泛应用于文本处理和字符串匹配领域。字典树是一种树形结构，用于存储字符串集合，并支持高效的字符串查找和前缀匹配。AC自动机是一种扩展的字典树，它在字典树的基础上增加了失败指针，支持高效的字符串模式匹配。

本篇文章将深入探讨字典树和AC自动机的理论基础、实践应用以及比较和选择。通过深入理解这些数据结构的原理和应用场景，读者可以掌握在不同场景下选择最合适的数据结构，提升文本处理和字符串匹配的效率。

# 2. 字典树的理论基础

### 2.1 字典树的基本概念和结构

字典树，也称为前缀树或单词查找树，是一种用于存储和检索字符串的树形数据结构。其基本思想是将字符串中的字符作为树中的节点，并通过节点之间的边来表示字符之间的顺序关系。

字典树的每个节点包含以下信息：

- 字符：表示该节点代表的字符。
- 子节点：指向包含该字符后继字符的子节点。
- 终止标志：指示该节点是否表示一个完整字符串的末尾。

一个字典树的示例如下：

      root
     /  \
    a    b
   / \   / \
  t   n  a  t
 / \
c   k

该字典树存储了字符串 "cat"、"bat"、"tack"。

### 2.2 字典树的插入、删除和查找算法

**插入算法**

插入一个新字符串到字典树中，需要从根节点开始，依次遍历字符串中的字符。如果当前节点不存在对应字符的子节点，则创建一个新的子节点并将其添加到当前节点。如果当前节点已存在对应字符的子节点，则继续遍历该子节点。当遍历到字符串末尾时，将当前节点的终止标志设置为 True。

def insert(self, word):
    curr = self.root
    for char in word:
        if char not in curr.children:
            curr.children[char] = TrieNode()
        curr = curr.children[char]
    curr.is_word = True

**删除算法**

删除一个字符串从字典树中，需要从根节点开始，依次遍历字符串中的字符。如果当前节点不存在对应字符的子节点，则返回 False，表示该字符串不存在于字典树中。如果当前节点已存在对应字符的子节点，则继续遍历该子节点。当遍历到字符串末尾时，将当前节点的终止标志设置为 False。如果当前节点没有其他子节点，则将其从父节点中删除。

def delete(self, word):
    if not self.search(word):
        return False

    curr = self.root
    for char in word:
        curr = curr.children[char]
        curr.count -= 1

    curr.is_word = False
    if curr.count == 0:
        del curr.parent.children[curr.char]
    return True

**查找算法**

查找一个字符串是否存在于字典树中，需要从根节点开始，依次遍历字符串中的字符。如果当前节点不存在对应字符的子节点，则返回 False，表示该字符串不存在于字典树中。如果当前节点已存在对应字符的子节点，则继续遍历该子节点。当遍历到字符串末尾时，如果当前节点的终止标志为 True，则返回 True，表示该字符串存在于字典树中。

def search(self, word):
    curr = self.root
    for char in word:
        if char not in curr.children:
            return False
        curr = curr.children[char]
    return curr.is_word

# 3. AC自动机的理论基础

### 3.1 AC自动机的基本概念和结构

AC自动机（Aho-Corasick automaton）是一种有限状态自动机，用于高效地进行字符串匹配。它由以下组件组成：

- **状态集合 Q**：表示自动机的状态，其中一个状态为初始状态，一个或多个状态为接受状态。
- **输入字母表 Σ**：表示自动机可以识别的字符集合。
- **转移函数 δ：Q × Σ → Q**：给定一个状态和一个输入字符，返回一个新的状态。
- **失败函数 f：Q → Q**：给定一个状态，返回一个新的状态，表示该状态匹配失败后应该跳转到的状态。

AC自动机的结构类似于字典树，但它增加了失败函数，以提高字符串匹配的效率。失败函数将每个状态与一个“失败”状态关联起来，当自动机在当前状态匹配失败时，它将跳转到失败状态。

### 3.2 AC自动机的构建算法

AC自动机的构建算法基于以下步骤：

1. **创建初始状态**：将初始状态添加到状态集合 Q 中。
2. **插入模式字符串**：对于每个模式字符串，从初始状态开始，依次插入字符串中的每个字符。如果当前状态没有到该字符的转移，则创建一个新的状态并将其添加到 Q 中。
3. **计算失败函数**：对于每个状态 q，计算其失败函数 f(q)。f(q) 的计算方法如下：
- 如果 q 是初始状态，则 f(q) = 初始状态。
- 否则，令 p = f(q 的父状态)。
- 如果 p 中存在到该字符的转移，则 f(q) = p 中到该字符的转移状态。
- 否则，递归调用 f(p) 直到找到一个状态 p'，其中 p' 中存在到该字符的转移。然后，f(q) = p' 中到该字符的转移状态。

### 代码示例

以下 Python 代码展示了如何构建一个 AC 自动机：

class ACAutomaton:
    def __init__(self):
        self.states = [0]  # 初始状态
        self.failure = [0] * len(self.states)  # 失败函数

    def insert(self, pattern):
        state = 0
        for char in pattern:
            if self.states[state].get(char) is None:
                self.states[state][char] = len(self.states)
                self.states.append({