渐近线与对称性：探索余切函数图像的隐秘特征

# 1. 余切函数及其图像

余切函数，记为 tan(x)，是三角函数中的一种，定义为对边与邻边的比值。其图像是一个周期性的波形，在原点处具有奇点。

**图像特性：**

* **周期性：**余切函数以 π 为周期，即 tan(x + π) = tan(x)。
* **奇函数：**余切函数关于原点对称，即 tan(-x) = -tan(x)。
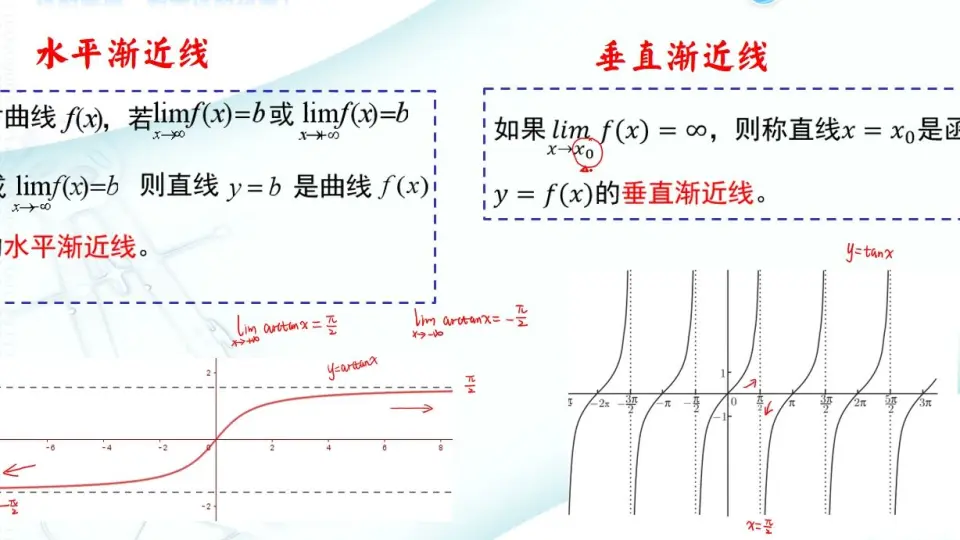
* **渐近线：**余切函数图像在 x = (2n + 1)π/2 (n 为整数) 处具有垂直渐近线，在 y = ±∞ 处具有水平渐近线。

# 2. 余切函数图像的边界

### 2.1 垂直渐近线：无穷大处的极限

**定义：**垂直渐近线是指当自变量趋于无穷大时，函数图像无限接近的竖直线。

**余切函数的垂直渐近线：**

tan(x) 的垂直渐近线为 x = π/2 + kπ，其中 k 为任意整数。

**证明：**

当 x 趋于 π/2 + kπ 时，tan(x) 的分子 sin(x) 趋于 1，分母 cos(x) 趋于 0。因此，tan(x) 趋于无穷大。

**代码示例：**

import numpy as np
import matplotlib.pyplot as plt

# 定义 x 轴范围
x = np.linspace(-10, 10, 1000)

# 计算 tan(x)
y = np.tan(x)

# 绘制 tan(x) 图像
plt.plot(x, y)

# 添加垂直渐近线
plt.axvline(x=np.pi/2, color='r', linestyle='--')
plt.axvline(x=np.pi/2 + np.pi, color='r', linestyle='--')

plt.show()

**逻辑分析：**

* `np.linspace(-10, 10, 1000)` 创建一个包含 1000 个值的 x 轴范围，从 -10 到 10。
* `np.tan(x)` 计算 x 轴上的每个点的正切值。
* `plt.plot(x, y)` 绘制 tan(x) 图像。
* `plt.axvline(x=np.pi/2, color='r', linestyle='--')` 和 `plt.axvline(x=np.pi/2 + np.pi, color='r', linestyle='--')` 添加垂直渐近线。

### 2.2 水平渐近线：无穷小处的极限

**定义：**水平渐近线是指当自变量趋于无穷小或无穷大时，函数图像无限接近的水平线。

**余切函数的水平渐近线：**

tan(x) 没有水平渐近线。

**证明：**

当 x 趋于无穷小或无穷大时，tan(x) 的分子 sin(x) 和分母 cos(x) 都趋于无穷大。因此，tan(x) 的极限不存在。

**代码示例：**

import numpy as np
import matplotlib.pyplot as plt

# 定义 x 轴范围
x = np.linspace(-10, 10, 1000)

# 计算 tan(x)
y = np.tan(x)

# 绘制 tan(x) 图像
plt.plot(x, y)

# 添加