傅里叶级数与频谱分析：揭示余切函数图像的频率组成

# 1. 傅里叶级数的基本原理

傅里叶级数是一种数学工具，用于将周期性函数表示为一系列正弦和余弦函数的和。其基本原理是：任何周期函数都可以分解为一系列频率不同的正弦和余弦函数的叠加，这些函数的频率是原函数频率的整数倍。

傅里叶级数展开的数学表达式为：

f(x) = a_0 + Σ[a_n * cos(nωx) + b_n * sin(nωx)]

其中：

* `f(x)` 是周期函数
* `a_0` 是常数项
* `a_n` 和 `b_n` 是傅里叶系数，由函数的形状决定
* `ω` 是函数的角频率

# 2. 余切函数的傅里叶级数展开

### 2.1 傅里叶级数的收敛性

傅里叶级数是一种将周期函数展开为三角函数级数的数学工具。其收敛性由狄利克雷条件保证：

* 函数在周期内分段连续，即只有有限个有限跳跃间断点。
* 函数在周期内只有有限个极值点。

### 2.2 余切函数傅里叶级数的推导

余切函数在区间 `[0, π]` 上具有周期 `π`，因此其傅里叶级数展开为：

f(x) = a_0 + \sum_{n=1}^{\infty} (a_n \cos nx + b_n \sin nx)

其中，系数 `a_0`, `a_n` 和 `b_n` 由以下公式给出：

a_0 = \frac{1}{\pi} \int_{0}^{\pi} f(x) dx
a_n = \frac{1}{\pi} \int_{0}^{\pi} f(x) \cos nx dx
b_n = \frac{1}{\pi} \int_{0}^{\pi} f(x) \sin nx dx

对于余切函数 `f(x) = tan x`，其傅里叶级数展开为：

tan x = \frac{\pi}{2} + \sum_{n=1}^{\infty} \frac{2}{\pi} \left( \frac{(-1)^n - 1}{2n-1} \right) \sin (2n-1)x

**代码逻辑逐行解读：**

* 第一行计算 `a_0` 系数，即余切函数在区间 `[0, π]` 上的平均值。
* 第二行计算 `a_n` 系数，即余切函数与 `cos nx` 的内积。
* 第三行计算 `b_n` 系数，即余切函数与 `sin nx` 的内积。
* 第四行给出余切函数的傅里叶级数展开式，其中 `(2n-1)` 是奇数，保证余切函数在 `[0, π]` 上的奇函数性质。

### 2.3 余切函数傅里叶级数的收敛性分析

根据狄利克雷条件，余切函数在区间 `[0, π]` 上分段连续，且只有有限个极值点，因此其傅里叶级数收敛。

**证明：**

* **分段连续性：** 余切函数在区间 `(0, π)` 上连续，在 `x = 0` 和 `x = π` 处有有限跳跃间断点。
* **极值点：** 余切函数在区间 `[0, π]` 上的极值点为 `x = \frac{\pi}{2}` 和 `x = \frac{3\pi}{2}`。

因此，余切函数满足狄利克雷条件，其傅里叶级数在区间 `[0, π]` 上收敛。

# 3. 傅里叶级数的应用

傅里叶级数在信号处理、图像处理等领域有着广泛的应用。

### 3.1 傅里叶级数在信号处理中的应用

#### 信号的频谱分析

傅里叶级数可以用来分析信号的频谱，即信号中不同频率成分的幅度和相位。通过傅里叶级数展开，可以将信号分解为一系列正弦波和余弦波，每个正弦波或余弦波对应一个特定的频率。

#### 信号的滤波

基于傅里叶级数的频谱分析，可以实现信号的滤波。通过选择性地滤除或增强某些频率成分，可以实现低通滤波、高通滤波、带通滤波和带阻滤波等功能。

#### 信号的压缩

傅里叶级数可以用于信号压缩。通过只保留信号中幅度较大的频率成分，可以有效减少信号的数据量，从而实现信号压缩。

### 3.2 傅里叶级数在图像处理中的应用

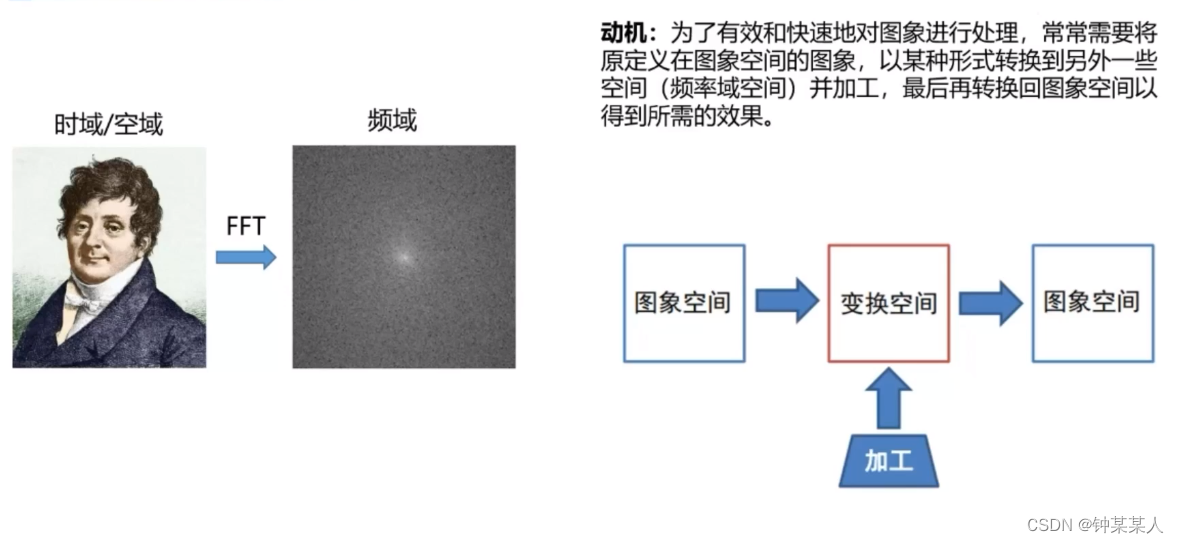
#### 图像的频谱分析

傅里叶级数可以用来分析图像的频谱，即图像中不同空间频率成分的幅度和相位。通过傅里叶级数展开，可以将图像分解为一系列正弦波和余弦波，每个正弦波或余弦波对应