三角学、微积分和工程中的余切函数图像：揭开函数的应用之谜

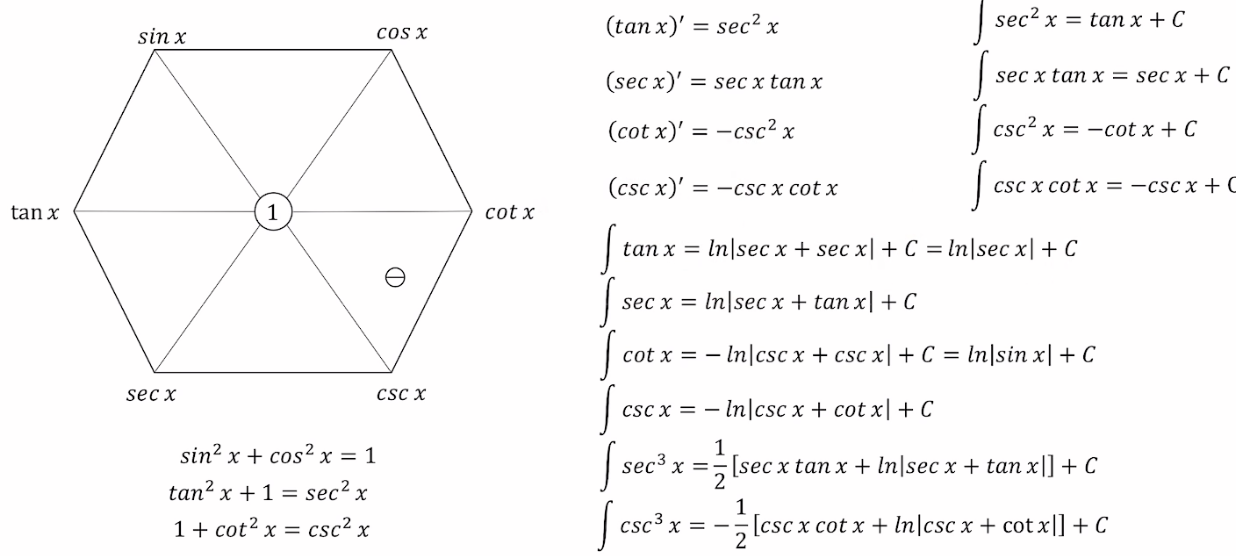
# 1. 余切函数的数学基础**

余切函数（tan），是三角学中一个重要的函数，定义为对边与邻边的比值。它与正弦函数（sin）和余弦函数（cos）密切相关，是三角恒等式和微积分中的关键函数。

在直角三角形中，余切函数表示斜边与对角的比值，即：tan θ = 对边 / 邻边。余切函数的范围为实数集，其图像是一个周期性函数，在奇数倍 π / 2 处有垂直渐近线。

# 2.1 微分和积分中的余切函数

### 2.1.1 余切函数的导数和积分

**导数：**

余切函数的导数由下式给出：

f(x) = tan(x)
f'(x) = sec^2(x)

**积分：**

余切函数的积分由下式给出：

∫ tan(x) dx = ln|sec(x)| + C

其中，C 是积分常数。

### 2.1.2 余切函数在极限和连续性中的应用

**极限：**

* 当 x 趋近于 π/2 时，tan(x) 趋近于无穷大。
* 当 x 趋近于 -π/2 时，tan(x) 趋近于负无穷大。

**连续性：**

余切函数在实数集上是连续的，除了在奇异点 x = π/2 和 x = -π/2。

**参数说明：**

* **x：**自变量，表示弧度。

**代码块：**

import numpy as np

# 计算余切函数的导数
x = np.linspace(-np.pi/2, np.pi/2, 100)
y = np.tan(x)
dydx = np.gradient(y, x)

# 绘制余切函数及其导数
import matplotlib.pyplot as plt
plt.plot(x, y, label="tan(x)")
plt.plot(x, dydx, label="d/dx tan(x)")
plt.legend()
plt.show()

**逻辑分析：**

* 使用 NumPy 库生成自变量 x 的值域。
* 计算余切函数 y 和其导数 dydx。
* 使用 Matplotlib 绘制余切函数及其导数的图像。

**表格：**

| **性质** | **余切函数** |
|---|---|
| 导数 | sec^2(x) |
| 积分 | ln|sec(x)| + C |
| 极限 | x → π/2: ∞, x → -π/2: -∞ |
| 连续性 | 实数集上连续，奇异点 x = π/2 和 x = -π/2 |

# 3.1 电路分析中的余切函数

#### 3.1.1 交流电路中的阻抗和相位角

在交流电路中，余切函数用于计算阻抗和相位角。阻抗是电路对交流电阻抗，相位角是电流和电压之间的相位差。

**阻抗计算：**

在交流电路中，阻抗 Z 由电阻 R、电感 L 和电容 C 决定，其计算公式为：

Z = √(R^2 + (XL - XC)^2)

其中：

* XL = ωL 是电感感抗，ω 是角频率
* XC = 1/(ωC) 是电容容抗

**相位角计算：**

相位角 φ 由阻抗 Z 和电感感抗 XL 与电容容抗 XC 之差决定，其计算公式为：

φ = arctan((XL - XC) / R)

#### 3.1.2 余切函数在谐振频率和品质因数中的应用

**谐振频率：**

谐振频率是电路中阻抗最小的频率，此时电感感抗和电容容抗相等。谐振频率 f0 的计算公式为：

f0 = 1/(2π√LC)

**品质因数：**

品质因数 Q 是衡量电路选择性的一种指标，其计算公式为：

Q = ω0L/R

其中 ω0 是谐振角频率。

品质因数越高，电路选择性越好，即电路对特定频率的响应更强。

# 4. 余切函数的图形化表示

### 4.1 余切函数的图像绘制

#### 4.1.1 余切函数的周期性和奇偶性

余切函数是一个周期函数，其周期为 π。这意味着对于任何实数 x，都有 tan(x + π) = tan(x)。

余切函数也是一个奇函数，这意味着对于任何实数 x，都有 tan(-x) = -tan(x)。

#### 4.1.2 余切函数的渐近线和拐点

余切函数有两个垂直渐近线，分别为 x = π/2 和 x = 3π/2。这些渐近线表示余切函数在这些点处不存在。

余切函数在 x = 0 处有一个拐点。在拐点处，余切函数的导数为 0，并且函数的曲率发生变化。

### 4.2 余切函数图像的变换

#### 4.2.1 平移、缩放和反射变换

余切函数图像可以通过平移、缩放和反射进行变换。

* 平移：通过添加或减去常数来平移余切函数图像。
* 缩放：通过乘以常数来缩放余切函数图像。
* 反射：通过在 x 轴或 y 轴上反射余切函数图像。

#### 4.2.2 余切函数图像的组合和反函数

余切函数图像可以通过组合和反函数进行变换。

* 组合：通过将余切函数与其他函数组合来创建新的函数。
* 反函数：通过求余切函数的反函数来创建新的函数。

### 代码示例

import numpy as np
import matplotlib.pyplot as plt

# 绘制余切函数图像
x = np.linspace(-np.pi, np.pi, 100)
y = np.tan(x)

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('tan(x)')
plt.title('余切函数图像')
plt.show()

**代码逻辑分析：**

* `np.linspace(-np.pi, np.pi, 100)` 创建一个从 -π 到 π 的 100 个点的均匀间隔数组。
* `np.tan(x)` 计算数组中每个点的余切值。
* `plt.plot(x, y)` 绘制余切函数图像。
* `plt.xlabel('x')` 和 `plt.ylabel('tan(x)')` 设置 x 轴和 y 轴的标签。
* `plt.title('余切函数图像')` 设置图像的标题。
* `plt.show()` 显示图像。

### 表格示例

| 变换类型 | 变换公式 |
|---|---|
| 平移 | tan(x + c) |
| 缩放 | tan(cx) |
| 反射（x 轴） | -tan(x) |
| 反射（y 轴） | tan(-x) |

### 流程图示例

graph LR
subgraph 余切函数图像的变换
    A[平移] --> B[缩放]
    B --> C[反射]
    C --> D[组合]
    D --> E[反函数]
end

# 5. 余切函数的应用拓展**

### 5.1 余切函数在信号处理中的应用

#### 5.1.1 傅里叶变换中的余切函数

傅里叶变换是一种将时域信号转换为频域表示的数学工具。余切函数在傅里叶变换中扮演着重要角色，它可以用来表示奇偶信号的虚部。

对于一个实值信号 `x(t)`，其傅里叶变换为：

X(f) = ∫[-∞,∞] x(t) e^(-2πift) dt

其中 `f` 是频率。

如果 `x(t)` 是一个奇函数，即 `x(-t) = -x(t)`，那么其傅里叶变换的虚部为：

Im[X(f)] = ∫[-∞,∞] x(t) sin(2πift) dt

此时，余切函数 `cot(πf)` 可以用来表示虚部：

Im[X(f)] = 2cot(πf) ∫[0,∞] x(t) cos(2πift) dt

#### 5.1.2 余切函数在滤波器设计中的作用

余切函数在滤波器设计中也具有重要应用。例如，在带通滤波器中，余切函数可以用来实现带通响应。

一个带通滤波器的传递函数可以表示为：

H(f) = cot(π(f - f0)/B)

其中 `f0` 是中心频率，`B` 是带宽。

该滤波器将通过中心频率 `f0` 附近的频率成分，而抑制其他频率成分。

### 5.2 余切函数在计算机图形学中的应用

#### 5.2.1 3D建模中的余切函数

在3D建模中，余切函数可以用来计算曲面上的法线向量。法线向量对于光照和阴影计算至关重要。

对于一个曲面 `S` 上的点 `p`，其法线向量 `n` 可以表示为：

n = cot(α) * (∂S/∂x) × (∂S/∂y)

其中 `α` 是曲面在点 `p` 处的法线角，`∂S/∂x` 和 `∂S/∂y` 是曲面在 `x` 和 `y` 方向上的偏导数。

#### 5.2.2 余切函数在光线追踪和渲染中的作用

在光线追踪和渲染中，余切函数可以用来计算光线与曲面的交点。

对于一条光线 `r` 和一个曲面 `S`，其交点 `p` 可以表示为：

p = r(t)

其中 `t` 是光线与曲面相交的参数。

通过求解以下方程，可以得到 `t` 的值：

cot(α) * (r(t) - S(p)) · (∂S/∂x) × (∂S/∂y) = 0