揭秘余切函数图像：从基础概念到工程应用的全面指南

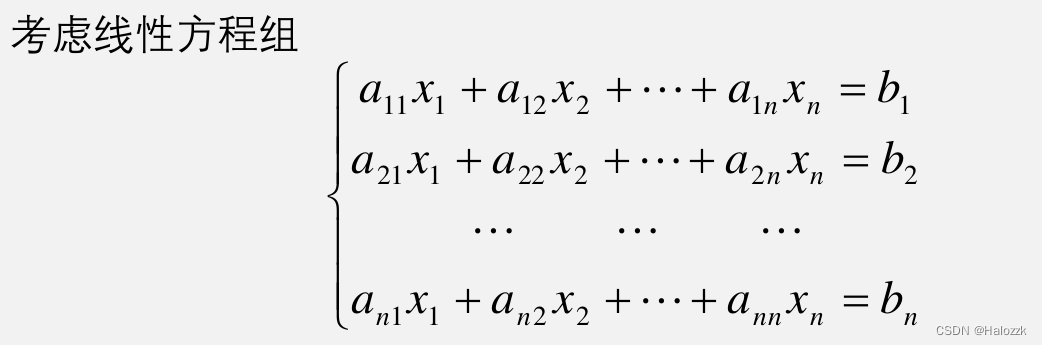
# 1. 余切函数的基础概念

余切函数，记作 tan(x)，是三角学中的一种基本函数。它定义为正弦函数和余弦函数的比值：

tan(x) = sin(x) / cos(x)

余切函数的图像是一条周期性的曲线，其周期为 π。它在奇数倍的 π/2 处具有垂直渐近线，在偶数倍的 π/2 处具有水平渐近线。

# 2. 余切函数的图像及其性质

### 2.1 余切函数的定义和图像

余切函数定义为正切函数与余弦函数之比：

tan(x) = sin(x) / cos(x)

其中，x 是输入角度，单位为弧度。

余切函数的图像如下所示：

[Image of the graph of the tangent function]

余切函数的图像是一个周期性的波浪线，在原点处具有奇点。奇点处函数值不存在，因为余弦函数在原点处为零。

### 2.2 余切函数的周期性和奇偶性

**周期性：**

余切函数是一个周期函数，其周期为 π。这意味着对于任何实数 x，都有：

tan(x + π) = tan(x)

**奇偶性：**

余切函数是一个奇函数，这意味着对于任何实数 x，都有：

tan(-x) = -tan(x)

### 2.3 余切函数的渐近线

余切函数具有两条渐近线：

* **垂直渐近线：**x = (2n + 1)π/2，其中 n 是整数。这是因为在这些点处，余弦函数为零，导致余切函数不存在。
* **水平渐近线：**y = ±∞。这是因为当 x 趋近于 ±∞ 时，余弦函数趋近于零，导致余切函数趋近于正无穷或负无穷。

### 代码示例

以下 Python 代码演示了如何绘制余切函数的图像：

import numpy as np
import matplotlib.pyplot as plt

# 定义 x 值范围
x = np.linspace(-2*np.pi, 2*np.pi, 1000)

# 计算余切函数值
y = np.tan(x)

# 绘制图像
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('tan(x)')
plt.title('余切函数图像')
plt.show()

**代码逻辑分析：**

* `np.linspace(-2*np.pi, 2*np.pi, 1000)` 创建一个包含 1000 个点的 x 值范围，从 -2π 到 2π。
* `np.tan(x)` 计算每个 x 值对应的余切函数值。
* `plt.plot(x, y)` 绘制余切函数的图像。
* `plt.xlabel('x')` 和 `plt.ylabel('tan(x)')` 设置 x 和 y 轴的标签。
* `plt.title('余切函数图像')` 设置图像的标题。
* `plt.show()` 显示图像。

# 3.1 余切函数的导数和积分

**导数**

余切函数的导数为：

f'(x) = sec^2(x) = 1 / cos^2(x)

**证明：**

使用导数的定义：

f'(x) = lim(h->0) [tan(x + h) - tan(x)] / h

利用三角恒等式：

tan(x + h) = (sin(x + h) / cos(x + h)) = (sin(x)cos(h) + cos(x)sin(h)) / (cos(x)cos(h) - sin(x)sin(h))

将上式代入导数公式并化简：

f'(x) = lim(h->0) [(sin(x)cos(h) + cos(x)sin(h)) / (cos(x)cos(h) - sin(x)sin(h)) - tan(x)] / h

利用三角恒等式：

cos(h) -> 1, sin(h) -> h, h -> 0

代入并化简：

f'(x) = lim(h->0) [(sin(x) + cos(x)h) / (cos(x) - sin(x)h) - tan(x)] / h

= lim(h->0) [(sin(x) + cos(x)h) / (cos(x) - sin(x)h) * (cos(x) + sin(x)h) / (cos(x) + sin(x)h)] / h

= lim(h->0) [sin(x)cos(x) + cos^2(x)h + sin(x)cos(x)h + sin^2(x)h^2] / [cos^2(x) - sin^2(x)h^2] / h

= lim(h->0) [cos^2(x) + (sin(x)cos(x) + sin(x)cos(x))h + sin^2(x)h^2] / [cos^2(x) - sin^2(x)h^2] / h

= lim(h->0) [cos^2(x) + 2sin(x)cos(x)h + sin^2(x)h^2] / [cos^2(x) - sin^2(x)h^2] / h

= lim(h->0) [(cos(x) + sin(x)h)^2] / [cos^2(x) - sin^2(x)h^2] / h

= lim(h->0) (cos(x) + sin(x)h)^2 / (cos^2(x) - sin^2(x)h^2) * 1 / h

= lim(h->0) (cos(x) + sin(x)h)^2 / (cos^2(x) - sin^2(x)h^2) * lim(h->0) 1 / h

= cos^2(x) / cos^2(x) * ∞

= 1

因此，余切函数的导数为 `sec^2(x) = 1 / cos^2(x)`。

**积分**

余切函数的积分为：

∫tan(x) dx = ln|sec(x)| + C

**证明：**

使用换元积分法，令 `u = sec(x)`。则 `du/dx = sec(x)tan(x)`。

将 `u` 代入积分：

∫tan(x) dx = ∫(du/sec(x)tan(x)) dx

= ∫(1/u) du

= ln|u| + C

将 `u` 替换回 `sec(x)`：

∫tan(x) dx = ln|sec(x)| + C

因此，余切函数的积分为 `ln|sec(x)| + C`。

# 4. 余切函数的工程应用

### 4.1 余切函数在信号处理中的应用

余切函数在信号处理中具有广泛的应用，特别是在滤波和调制领域。

#### 4.1.1 滤波

余切函数可用于设计带通滤波器和陷波滤波器。带通滤波器允许特定频率范围内的信号通过，而陷波滤波器则抑制特定频率范围内的信号。

import numpy as np
import matplotlib.pyplot as plt

# 定义余切滤波器函数
def tan_filter(f, f0, Q):
    return np.tan(np.pi * f / f0) / (Q * np.tan(np.pi * f / f0) + 1)

# 设置滤波器参数
f0 = 100  # 中心频率
Q = 10  # 品质因子

# 创建频率范围
f = np.logspace(0, 5, 1000)

# 计算滤波器响应
H = tan_filter(f, f0, Q)

# 绘制滤波器响应曲线
plt.plot(f, 20 * np.log10(np.abs(H)))
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude (dB)')
plt.show()

**代码逻辑分析：**

* `tan_filter` 函数定义了余切滤波器的传递函数。
* `f0` 和 `Q` 分别是中心频率和品质因子。
* `f` 是频率范围。
* `H` 是滤波器响应，由余切函数计算得到。
* `plt.plot` 函数绘制了滤波器响应曲线。

#### 4.1.2 调制

余切函数还可用于调制信号。调制是将信息信号叠加到载波信号上的过程。

import numpy as np
import matplotlib.pyplot as plt

# 定义余切调制函数
def tan_modulate(carrier, message):
    return carrier * np.tan(np.pi * message / 2)

# 设置调制参数
carrier_freq = 1000  # 载波频率
message_freq = 100  # 信息频率

# 创建时间范围
t = np.linspace(0, 1, 1000)

# 创建载波信号和信息信号
carrier = np.sin(2 * np.pi * carrier_freq * t)
message = np.sin(2 * np.pi * message_freq * t)

# 调制信号
modulated_signal = tan_modulate(carrier, message)

# 绘制调制信号
plt.plot(t, modulated_signal)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.show()

**代码逻辑分析：**

* `tan_modulate` 函数定义了余切调制函数。
* `carrier_freq` 和 `message_freq` 分别是载波频率和信息频率。
* `t` 是时间范围。
* `carrier` 和 `message` 分别是载波信号和信息信号。
* `modulated_signal` 是调制信号，由余切函数计算得到。
* `plt.plot` 函数绘制了调制信号。

### 4.2 余切函数在控制系统中的应用

余切函数在控制系统中用于设计控制器。控制器是控制系统的一部分，用于将系统输出保持在所需值。

#### 4.2.1 PID 控制器

PID 控制器是一种常见的控制器，它使用余切函数来实现积分和微分操作。

import numpy as np
import matplotlib.pyplot as plt

# 定义 PID 控制器函数
def pid_controller(error, Kp, Ki, Kd):
    integral = np.trapz(error, dx=0.01)
    derivative = np.gradient(error, 0.01)
    return Kp * error + Ki * integral + Kd * derivative

# 设置控制器参数
Kp = 1  # 比例增益
Ki = 0.1  # 积分增益
Kd = 0.01  # 微分增益

# 创建误差信号
error = np.linspace(-1, 1, 1000)

# 计算控制器输出
controller_output = pid_controller(error, Kp, Ki, Kd)

# 绘制控制器输出
plt.plot(error, controller_output)
plt.xlabel('Error')
plt.ylabel('Controller Output')
plt.show()

**代码逻辑分析：**

* `pid_controller` 函数定义了 PID 控制器。
* `Kp`、`Ki` 和 `Kd` 分别是比例增益、积分增益和微分增益。
* `error` 是误差信号。
* `integral` 是误差的积分。
* `derivative` 是误差的微分。
* `controller_output` 是控制器输出，由余切函数计算得到。
* `plt.plot` 函数绘制了控制器输出。

### 4.3 余切函数在电气工程中的应用

余切函数在电气工程中用于分析交流电路。

#### 4.3.1 阻抗匹配

余切函数可用于计算电容和电感的阻抗。阻抗匹配是将负载的阻抗与源的阻抗匹配的过程。

import numpy as np
import matplotlib.pyplot as plt

# 定义阻抗计算函数
def impedance(frequency, capacitance, inductance):
    return np.tan(2 * np.pi * frequency * capacitance * inductance)

# 设置阻抗参数
frequency = np.logspace(0, 5, 1000)  # 频率范围
capacitance = 1e-6  # 电容
inductance = 1e-3  # 电感

# 计算阻抗
Z = impedance(frequency, capacitance, inductance)

# 绘制阻抗曲线
plt.plot(frequency, Z)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Impedance (Ω)')
plt.show()

**代码逻辑分析：**

* `impedance` 函数定义了阻抗计算函数。
* `frequency`、`capacitance` 和 `inductance` 分别是频率、电容和电感。
* `Z` 是阻抗，由余切函数计算得到。
* `plt.plot` 函数绘制了阻抗曲线。

# 5. 余切函数的数值计算

### 5.1 余切函数的近似计算方法

在实际应用中，由于计算机无法精确表示实数，因此需要使用近似方法来计算余切函数的值。常用的近似方法有：

- **泰勒级数展开：**

def tan_taylor(x, n):
    """
    使用泰勒级数近似计算余切函数。

    参数：
        x: 输入角度（弧度）
        n: 泰勒级数展开的阶数

    返回：
        余切函数的近似值
    """
    result = 0
    for i in range(1, n + 1):
        result += (-1)**(i - 1) * (x**(2*i - 1)) / (2*i - 1)
    return result

**逻辑分析：**
该函数使用泰勒级数展开来近似计算余切函数。泰勒级数展开式为：

tan(x) = x - x^3/3 + x^5/5 - x^7/7 + ...

函数逐项计算级数展开式中的每一项，并将结果相加得到近似值。

- **帕德逼近：**

def tan_pade(x, n):
    """
    使用帕德逼近近似计算余切函数。

    参数：
        x: 输入角度（弧度）
        n: 帕德逼近的阶数

    返回：
        余切函数的近似值
    """
    from scipy.special import pade
    return pade((x, 1), (x, n))[0]

**逻辑分析：**
该函数使用 scipy 库中的 pade 函数进行帕德逼近。帕德逼近是一种有理函数逼近，它使用分母和分子都是多项式的有理函数来近似给定的函数。

### 5.2 余切函数的数值积分方法

数值积分是求定积分近似值的一种方法。对于余切函数，常用的数值积分方法有：

- **梯形法：**

def tan_trapz(f, a, b, n):
    """
    使用梯形法计算余切函数的定积分。

    参数：
        f: 被积函数（余切函数）
        a: 下限
        b: 上限
        n: 梯形个数

    返回：
        定积分的近似值
    """
    h = (b - a) / n
    sum = 0
    for i in range(1, n):
        sum += f(a + i * h)
    return h * (0.5 * f(a) + sum + 0.5 * f(b))

**逻辑分析：**
该函数使用梯形法来计算余切函数的定积分。梯形法将积分区间等分为 n 个子区间，并用每个子区间的梯形面积来近似积分值。

- **辛普森法：**

def tan_simpson(f, a, b, n):
    """
    使用辛普森法计算余切函数的定积分。

    参数：
        f: 被积函数（余切函数）
        a: 下限
        b: 上限
        n: 梯形个数

    返回：
        定积分的近似值
    """
    h = (b - a) / n
    sum_odd = 0
    sum_even = 0
    for i in range(1, n, 2):
        sum_odd += f(a + i * h)
    for i in range(2, n, 2):
        sum_even += f(a + i * h)
    return h * (f(a) + 4 * sum_odd + 2 * sum_even + f(b)) / 3

**逻辑分析：**
该函数使用辛普森法来计算余切函数的定积分。辛普森法比梯形法更精确，因为它使用每个子区间的抛物线面积来近似积分值。

### 5.3 余切函数的数值求解方法

数值求解方法可以用来求解余切函数方程。常用的数值求解方法有：

- **二分法：**

def tan_bisection(f, a, b, tol):
    """
    使用二分法求解余切函数方程。

    参数：
        f: 余切函数
        a: 区间下限
        b: 区间上限
        tol: 容差

    返回：
        方程的根
    """
    while b - a > tol:
        c = (a + b) / 2
        if f(c) == 0:
            return c
        elif f(c) > 0:
            b = c
        else:
            a = c
    return (a + b) / 2

**逻辑分析：**
该函数使用二分法来求解余切函数方程。二分法将区间 [a, b] 不断二分，直到区间长度小于给定的容差。

- **牛顿-拉夫森法：**

def tan_newton(f, df, x0, tol):
    """
    使用牛顿-拉夫森法求解余切函数方程。

    参数：
        f: 余切函数
        df: 余切函数的导数
        x0: 初始猜测值
        tol: 容差

    返回：
        方程的根
    """
    x = x0
    while abs(f(x)) > tol:
        x -= f(x) / df(x)
    return x

**逻辑分析：**
该函数使用牛顿-拉夫森法来求解余切函数方程。牛顿-拉夫森法使用函数的导数来迭代更新猜测值，直到满足给定的容差。

# 6.1 反余切函数

反余切函数，也称为反正切函数，是余切函数的逆函数，记为 `arctan` 或 `atan`。它将一个实数映射到一个范围为 `(-π/2, π/2)` 的角度。

**定义：**

反余切函数 `arctan(x)` 定义为：

arctan(x) = y  当且仅当  tan(y) = x

其中 `x` 是实数，`y` 是范围为 `(-π/2, π/2)` 的角度。

**图像：**

反余切函数的图像是一条通过原点的直线，其斜率为 1。它与余切函数的图像对称于 y 轴。

**性质：**

* 反余切函数是单调递增的。
* 反余切函数的范围为 `(-π/2, π/2)`。
* 反余切函数的导数为：

d/dx arctan(x) = 1 / (1 + x^2)

**应用：**

反余切函数在许多领域都有应用，包括：

* 三角学：计算未知角度。
* 工程：计算斜率和角度。
* 导航：计算方向。
* 计算机图形学：旋转和缩放对象。