【网络流算法解析】：Python实现网络流量优化策略

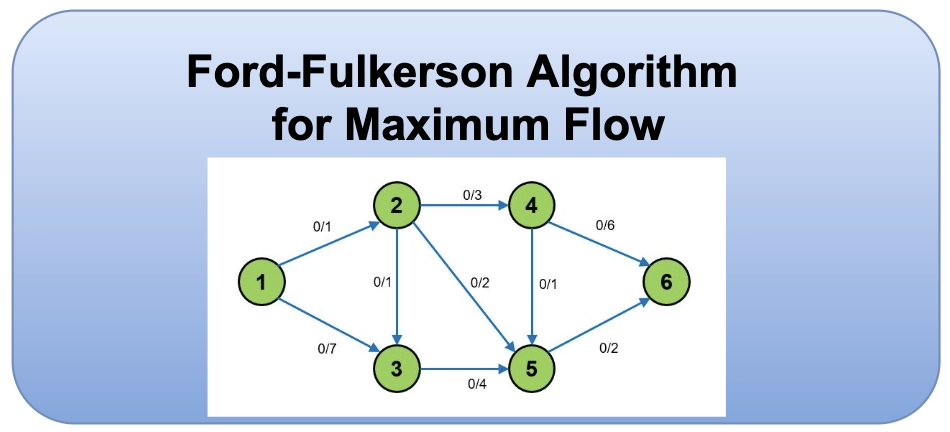
# 1. 网络流算法的理论基础

## 1.1 网络流问题的定义

在网络流算法中，我们将网络流问题定义为一种图论中的应用问题。它由一个有向图构成，图中的边有其容量限制，节点分为源点和汇点。源点表示资源的起始位置，而汇点表示资源的接收点。而网络流问题关注的是如何在不违反容量限制的前提下，从源点向汇点传递最大量的资源。

## 1.2 网络流问题的数学模型

数学上，网络流问题可以通过线性规划来表示。一个基本的网络流问题涉及到图G(V,E)，其中V是节点集合，E是边集合。每条边(e,u,v)都有一个非负容量限制c(u,v)。流函数f(u,v)表示从节点u到节点v的流量，它满足以下两个条件：

1. 容量限制（Capacity Constraints）：对于所有(u,v) ∈ E，有0 ≤ f(u,v) ≤ c(u,v)。
2. 流量守恒（Flow Conservation）：对于所有u ∈ V-{s,t}（s是源点，t是汇点），有∑v:(v,u)∈E f(v,u) = ∑v:(u,v)∈E f(u,v)。

## 1.3 最大流问题的数学表述

最大流问题是网络流问题中最常见的形式之一。它寻求的是从源点s到汇点t的网络中，最大的流量值。数学上，我们希望最大化函数F = ∑v:(s,v)∈E f(s,v)。这个最大化过程必须在满足上述的容量限制和流量守恒的条件下完成。

总结起来，网络流算法是理解和优化网络资源传输的关键工具，其理论基础构成了后续章节深入分析和实现细节的基石。在IT行业中，网络流算法被广泛应用于数据网络的流量分析、网络设计、资源调度等多个领域，对有经验的从业者来说，理解这些基础概念是至关重要的。

# 2. Python网络流算法实现细节

### 2.1 网络流问题的数学模型

#### 2.1.1 流网络的定义和特性

流网络是一种有向图，其中每条边(u, v)都有一个非负容量c(u, v)，表示边能够传输的最大流量。一个流网络还包含一对特殊的节点：源点(s)和汇点(t)。在流网络中，流量必须从源点出发，并且最终流入汇点，不能在任何节点处产生或消失。

流网络的关键特性包括：
- **容量限制**：对于流网络中的任意一条边(u, v)，流f(u, v)不能超过该边的容量c(u, v)。
- **流量守恒**：对于除了源点和汇点外的每个节点v，流入节点v的流量总和必须等于流出该节点的流量总和，即满足流量守恒定律。

一个流f是定义在网络N上的一个函数，它满足以下两个条件：
- **容量限制**：对于所有的(u, v)属于网络N的边，有 0 ≤ f(u, v) ≤ c(u, v)。
- **流量守恒**：对于所有的节点v除了源点s和汇点t，有 ∑ f(u, v) = ∑ f(v, w)，即流入节点v的流量总和等于流出该节点的流量总和。

#### 2.1.2 最大流问题的数学表述

最大流问题是找到一个网络N中，从源点s到汇点t的最大可能流量的值。这个值是指网络中所有从源点出发的边中，流入汇点t的流量的总和的最大值。

用数学语言表达就是：找到一个流f，使得从s到t的流量总和（也就是流值）|f| = ∑ f(s, v) - ∑ f(v, s) 达到最大。

### 2.2 基础网络流算法的Python编码

#### 2.2.1 Ford-Fulkerson方法实现

Ford-Fulkerson方法是一种寻找网络中最大流的算法。它通过不断寻找增广路径（也就是从s到t的路径，且路径上每条边的剩余容量都不为零）并增加流量来逼近最大流值。

以下是Ford-Fulkerson方法的一个基本Python实现：

from collections import defaultdict

class Graph:
    def __init__(self, vertices):
        self.V = vertices
        self.graph = defaultdict(list)
    def add_edge(self, u, v, w):
        self.graph[u].append((v, w))
        self.graph[v].append((u, 0))
    def bfs(self, s, t, parent):
        visited = [False]*(self.V)
        queue = []
        queue.append(s)
        visited[s] = True
        while queue:
            u = queue.pop(0)
            for ind, val in enumerate(self.graph[u]):
                v, w = val
                if visited[v] == False and w > 0:
                    queue.append(v)
                    visited[v] = True
                    parent[v] = u
        return visited[t]

    def ford_fulkerson(self, source, sink):
        parent = [-1]*(self.V)
        max_flow = 0
        while self.bfs(source, sink, parent):
            path_flow = float('inf')
            s = sink
            while(s != source):
                path_flow = min(path_flow, self.graph[parent[s]][s][1])
                s = parent[s]
            max_flow += path_flow
            v = sink
            while(v != source):
                u = parent[v]
                self.graph[u][v][1] -= path_flow
                self.graph[v][u][1] += path_flow
                v = parent[u]
        return max_flow

# 示例使用：
g = Graph(6)
g.add_edge(0, 1, 16)
g.add_edge(0, 2, 13)
g.add_edge(1, 2, 10)
g.add_edge(1, 3, 4)
g.add_edge(2, 1, 9)
g.add_edge(2, 4, 14)
g.add_edge(3, 2, 7)
g.add_edge(3, 5, 20)
g.add_edge(4, 3, 4)
g.add_edge(4, 5, 18)
g.add_edge(5, 4, 6)

print("The maximum possible flow is %d " %g.ford_fulkerson(0, 5))

#### 2.2.2 Edmonds-Karp算法的实现

Edmonds-Karp算法是Ford-Fulkerson方法的一个具体实现，它使用广度优先搜索来寻找增广路径。

以下是Edmonds-Karp算法的一个基本Python实现：

def bfs(rGraph, s, t, parent):
    visited = [False] * len(rGraph)
    queue = []
    queue.append(s)
    visited[s] = True

    while queue:
        u = queue.pop(0)
        for ind, val in enumerate(rGraph[u]):
            if visited[ind] == False and val > 0:
                queue.append(ind)
                visited[ind] = True
                parent[ind] = u
    return visited[t]

def edmonds_karp(graph, source, sink):
    rGraph = [row[:] for row in graph]
    parent = [-1] * len(graph)
    max_flow = 0
    while bfs(rGraph, source, sink, parent):
        path_flow = float('inf')
        s = sink
        while(s != source):
            path_flow = min(path_flow, rGraph[parent[s]][s])
            s = parent[s]
        max_flow += path_flow
        v = sink
        while(v != source):
            u = parent[v]
            rGraph[u][v] -= path_flow
            rGraph[v][u] += path_flow
            v = parent[u]
    return max_flow

# 示例使用：
graph = [[0, 16, 13, 0, 0, 0],
         [0, 0, 10, 4, 0, 0],
         [0, 9, 0, 0, 14, 0],
         [0, 0, 7, 0, 4, 20],
         [0, 0, 0, 0, 0, 18],
         [0, 0, 0, 0, 6, 0]]
print("The maximum possible flow is %d " %edmonds_karp(graph, 0, 5))

#### 2.2.3 Dinic算法的Python实现

Dinic算法是另一种寻找最大流的算法。它比Edmonds-Karp算法更快，因为它不仅寻找单条增广路径，而是寻找层次图中的一组增广路径。层次图是通过对原始图进行分层，来限制搜索增广路径时的选择范围。

以下是Dinic算法的一个基本Python实现：

from collections import deque

def bfs(rGraph, s, t, parent):
    visited = [False] * len(rGraph)
    queue = deque()
    queue.append(s)
    visited[s] = True

    while queue:
        u = queue.popleft()
        fo