【PageRank算法实现】：Python网页排名算法全解析

# 1. PageRank算法的核心原理

## 1.1 PageRank简介
PageRank是谷歌搜索引擎的核心算法之一，由拉里·佩奇和谢尔盖·布林开发，目的是衡量网页的重要性。算法通过网页间的超链接关系来评估网页的重要性，本质上是一个概率矩阵的计算过程。

## 1.2 算法的数学基础
PageRank算法的基础在于认为被更多其他页面链接的页面更加重要。此算法可以视作一个马尔可夫链，其中网页是状态，链接则是状态间的转移概率。

## 1.3 PageRank的计算公式
PageRank值的计算公式是一个递归式，其本质是网页的重要性取决于链接到它的网页的重要性。公式中包含一个重要的参数：阻尼因子d，它模拟了用户点击链接时在网页间跳跃的可能性，通常设置为0.85。

通过以上核心原理的介绍，可以对PageRank算法有一个初步的理解，为后续更深入的讨论打下基础。在下一章中，我们将详细探讨PageRank的理论基础，并通过具体的数学模型来进行深入分析。

# 2. PageRank算法的理论基础

## 2.1 网络图论简介

### 2.1.1 图的基本概念和定义

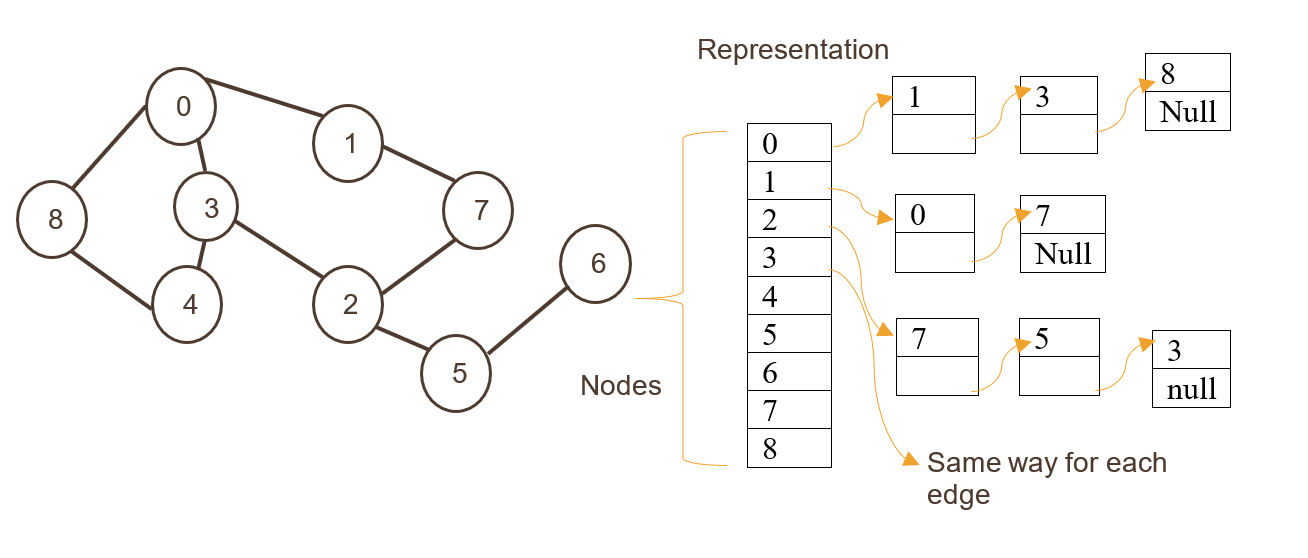
在数学和计算机科学领域中，图（Graph）是由一组顶点（也称为节点或点）和一组连接这些顶点的边组成的集合。图是网络分析和图算法中的基础概念，用于描述网络中的元素以及元素之间的关系。图可以用于模拟各种真实世界的问题，比如社交网络、交通网络、互联网等。

在图论中，顶点称为图的节点（Node），而连接节点的线段称为边（Edge）。根据边的特性，图可以被分为有向图（Directed Graph）和无向图（Undirected Graph）。在有向图中，边是有方向的，连接了两个节点，而无向图中的边则没有方向，连接的两个节点不区分顺序。

在PageRank算法中，图的概念尤为重要，因为网页之间的超链接关系可以被抽象为一个有向图，网页作为图中的节点，超链接则作为有向边。

### 2.1.2 有向图和无向图的区别

有向图（Directed Graph）和无向图（Undirected Graph）是图论中的两种基本图类型，它们的主要区别在于边的属性。

在无向图中，边是没有方向的，因此每条边连接的两个节点是互不可分的。在社交网络中，无向图常用来表示两个人之间的双向关系，比如“互为好友”的关系。

相对地，在有向图中，每条边都有一个方向，表示连接两个节点的单向关系。在互联网中，网页之间的链接关系就可以用有向图来表示。例如，网页A上有一个链接指向网页B，我们就说网页A到网页B有一条有向边。

有向图和无向图的差异对算法的实现和性能有很大影响。例如，在有向图中，顶点的入度（In-degree）和出度（Out-degree）成为重要的网络属性，而这些在无向图中并不适用。这些属性对于评估页面的重要性以及排名有着直接影响。

## 2.2 马尔可夫链与随机游走

### 2.2.1 马尔可夫链的基本性质

马尔可夫链是一类随机过程，它描述的是一个系统在一系列状态之间按一定概率转移的过程。在马尔可夫链中，下一个状态的概率只与当前状态有关，与之前的状态无关，这种性质称为马尔可夫性质（Markov Property）。这使得马尔可夫链具有了非常强大的预测能力。

马尔可夫链是PageRank算法中的核心数学概念。在互联网上，用户从一个网页跳转到另一个网页的行为可以通过马尔可夫链来模拟。每个网页都可以看作是一个状态，当用户访问一个网页并点击链接跳转到另一个网页时，就相当于从一个状态转移到另一个状态。

马尔可夫链的数学表达通常包括状态集合、转移矩阵以及概率分布。在PageRank算法中，网页的状态转移矩阵由网页之间的链接关系来决定。一个网页的PageRank值可以理解为用户在随机游走的过程中停留在该页面的概率。

### 2.2.2 随机游走模型及其数学表达

随机游走（Random Walk）是一种数学上的统计模型，它描述的是一个随机过程，即在一定规则下，一个过程或系统在状态空间中随机地移动。在PageRank算法中，我们假定用户在互联网上进行随机游走，即在网页间随机跳转。

当用户访问到一个网页时，他们有两种选择：点击链接跳转到其他网页，或者关闭浏览器离开当前网页。在这个过程中，如果用户选择了跳转，那么下一个访问的网页就是随机选择的，这可以被建模为一个马尔可夫过程。每个网页都可以视为一个状态，用户的行为可以视为在各个状态（网页）之间的转移。

数学上，可以使用状态转移矩阵来描述随机游走过程。设状态转移矩阵为P，其中P[i][j]表示从状态i转移到状态j的概率。在PageRank模型中，这个矩阵是通过网页之间的链接结构来定义的。对于一个网页i，它的PageRank值可以看做是用户在随机游走模型下停留在该网页的概率。

## 2.3 PageRank公式详解

### 2.3.1 权重的传递和分布

PageRank的核心思想是网页的重要性是通过链接关系来传递的。一个网页的重要性不仅取决于直接指向它的链接数，而且还取决于这些链接来源网页的重要程度。这样，链接就被视为一种“投票”，网页通过超链接将自身的权重传递给其他网页。

具体来说，如果一个权威页面有一个链接指向另一个页面，那么被链接的页面就可以获得一定的权威性。权重的这种传递是递归的，因为被链接的页面本身也可能会有链接指向其他页面。因此，整个互联网可以被视为一个巨大的链式反应，通过这种链接关系不断传递权重。

PageRank算法使用了一个迭代的过程来计算每个页面的权重。初始时，所有页面的权重可能被设定为相同的值。在每一轮迭代中，每个页面的权重根据来自其他页面的链接权重进行更新。权重的传递与分布遵循“传递和接收”的原则，即页面收到的链接权重与来源页面的权重成正比，并且与指向该页面的所有链接数量成反比。

### 2.3.2 阻尼因子的作用和影响

阻尼因子（damping factor）是PageRank算法中的一个关键参数，用于调整随机游走过程中的概率分布。阻尼因子通常被表示为一个介于0和1之间的值，记为d。在算法中，阻尼因子控制了用户在随机游走过程中继续浏览网页（继续点击链接）的概率。

如果阻尼因子设置为1，则意味着用户将永远沿着网页间的链接进行浏览，没有离开的可能性。而阻尼因子为0时，则用户在访问一个网页后总是会立即跳转到另一个新的页面。通常情况下，阻尼因子会选择一个介于两者之间的值，比如0.85，这意味着用户在当前网页上停止继续点击链接，即退出浏览的概率是15%。

阻尼因子的存在使得PageRank算法更加符合实际情况。在现实世界中，用户浏览网页并不总是完全依赖于链接的指引，他们可能会直接输入网址、使用书签或者搜索来访问网页，而不是一直跟随链接跳转。阻尼因子的引入，可以模拟这种行为，保证了算法的稳定性和实用性。

阻尼因子对PageRank计算结果的影响是显著的。较小的阻尼因子会导致排名更加集中，只有少数页面会获得较高的权重；而较大的阻尼因子则会促进权重的更广泛分布，使得更多页面能够获得一定的排名。在实际应用中，选择合适的阻尼因子对于平衡排名的集中与分散程度至关重要。

在这一章节中，我们深入探讨了PageRank算法的理论基础，从网络图论到马尔可夫链与随机游走，再到PageRank公式的权重传递和阻尼因子。这些理论知识是理解和应用PageRank算法的关键。在下一章节中，我们将深入到PageRank算法的具体Python实现，以及如何优化算法性能和提高结果的准确性。

# 3. PageRank算法的Python实现

## 3.1 环境搭建与数据准备

### 3.1.1 安装Python和相关库

为了实现PageRank算法，第一步是搭建一个适当的开发环境。这包括安装Python以及用于数据处理和算法实现的相关库。推荐使用Python 3.x版本，因为它是最新的稳定版本，拥有广泛的社区支持和丰富的第三方库。

首先，确保你的系统已经安装了Python。接下来，安装几个关键的第三方库，包括NumPy、SciPy和Matplotlib，这些库将用于科学计算和数据可视化。

pip install numpy scipy matplotlib

对于PageRank的实现，我们将使用NumPy来处理矩阵运算，SciPy库中包含了一些高级数学函数，可以帮助我们更方便地实现PageRank算法。Matplotlib库则用于生成算法结果的图表。

### 3.1.2 数据集的选择和预处理

为了测试PageRank算法，我们需要一个网页链接结构的数据集。在实际场景中，这可以是从网站爬取的数据。为了简化，我们可以使用一个较小的示例数据集。

数据预处理的目标是将网页链接结构转换为一个邻接矩阵。在这个矩阵中，如果网页A链接到网页B，则矩阵中的对应元素设置为1，否则为0。需要注意的是，真实世界的数据往往包含无效链接和孤立节点，因此预处理步骤还要包括数据的清洗和规范化。

这里给出一个简单的示例邻接矩阵：

import numpy as np

# 示例邻接矩阵，代表网页链接结构
adj_matrix = np.array([
    [0, 1, 0, 0],
    [1, 0, 1, 0],
    [0, 1, 0, 1],
    [0, 0, 1, 0]
])

print(adj_matrix)

这个邻接矩阵代表了四个网页之间的链接关系，其中网页1链接到网页2，网页2链接到网页1和网页3，依此类推。预处理过程中，你可能需要处理一些特殊情况，如避免自环（网页链接到自己）和处理重定向。

## 3.2 PageRank算法的基础编码

### 3.2.1 邻接矩阵的构建和初始化

在构建邻接矩阵之后，我们需要初始化PageRank值。通常，可以将所有页面的PageRank值设为1，然后通过迭代更新这些值直到收敛。

代码示例如下：

def pagerank_init(n):
    # 初始化PageRank值
    return np.ones(n) / n

# 假设我们有4个页面
n = 4
ranks = pagerank_init(n)
print(ranks)

### 3.2.2 迭代计算过程的实现

接下来是实现PageRank算法的核心迭代过程。PageRank的计算涉及到不断更新每个页面的分数，基于它收到的链接数以及来源页面的重要性。