【图社区检测】：Python在图同构性检测中的应用

# 1. 图同构性检测基础

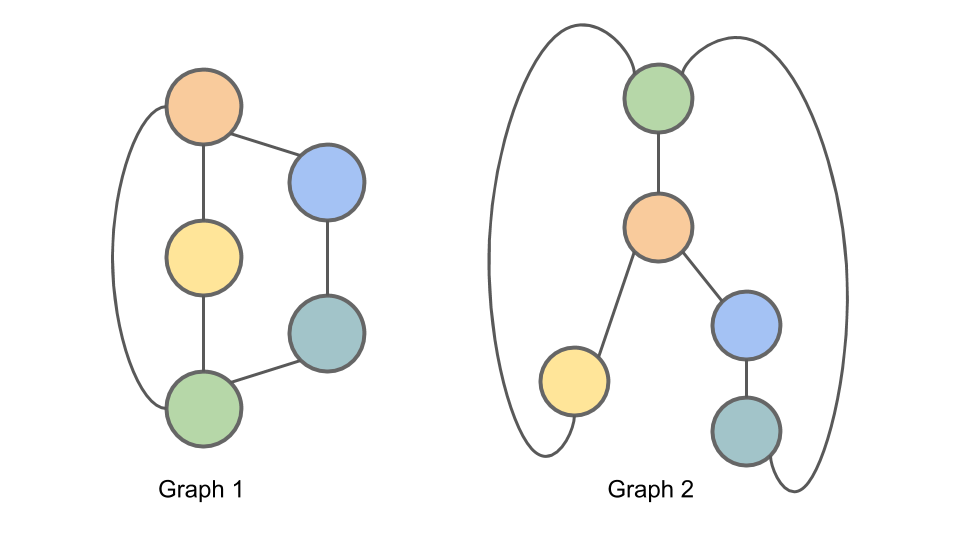
图同构性检测是图论和计算机科学中的一个核心问题，它关注的是在不考虑节点标签的情况下，确定两个图是否有相同的拓扑结构。本章将介绍图同构性检测的基础概念，为后续章节深入探讨算法细节和应用实践打下坚实的基础。

## 1.1 图同构性的定义
图同构性指的是两个图之间存在一一对应的关系，使得一个图中的任意两个顶点相邻当且仅当另一个图中对应顶点也是相邻的。尽管顶点的标识和编号可以不同，但其连接方式和拓扑结构是相同的。检测图的同构性是困难的，尤其是对于大型图，由于其组合复杂性，可能需要非常高的计算资源。

## 1.2 同构性检测的重要性
同构性检测在多个领域有广泛应用，如网络拓扑分析、化学信息学中的分子结构比较、以及计算机视觉中的图形匹配等。理解了图同构性，我们能够解决诸多问题，如检测恶意软件在网络中的传播模式、分析复杂化学反应过程中的分子相似性，以及图形图像识别中的模式匹配问题等。

在下一章节，我们将深入探索图同构性的理论基础，以及相关的判定方法和算法概述。

# 2. 图同构性检测的理论基础

## 2.1 图的基本概念和性质

### 2.1.1 图的定义和分类

在图论中，图是由节点（顶点）以及连接这些节点的边组成的数学结构。形式化地说，一个图G可以被定义为一个二元组(G, E)，其中G是节点集，E是连接节点的边集。根据边的性质，图可以分为无向图和有向图。无向图中边是没有方向的，而有向图中的边具有明确的方向性。

图也可以根据边的存在与否被分类为简单图或多重图。简单图中任意两个顶点间最多有一条边，而多重图中顶点之间可能有多条边。在图同构性检测中，不同类型的图可能需要不同的处理策略和算法。

### 2.1.2 图的同构性质和判定方法

同构图是指两个图之间存在一一对应的关系，使得它们的邻接关系完全相同。简单来说，如果可以将图G1中的顶点重新标记为图G2中的顶点，使得G1中的每条边在G2中都有对应的边，那么这两个图是同构的。

判定两个图是否同构是NP难问题，常用的判定方法包括基于顶点度序列的方法、基于邻接矩阵的方法等。最近的研究还包括利用图的频谱特征进行同构性判定。

## 2.2 图同构性检测算法概述

### 2.2.1 算法复杂度与图规模的关系

图同构性检测的算法复杂度随着图的规模增长而显著增加。对于小规模的图，可以通过穷举所有可能的顶点映射来验证同构性，但这种方法的复杂度是图顶点数阶乘级别的，对于大规模图来说是不可行的。

针对复杂度问题，算法研究者提出了很多优化策略，比如利用回溯搜索的启发式算法、基于图的不变量比较的算法等。随着算法的优化和计算机性能的提高，原本无法处理的复杂图现在也有了被分析的可能性。

### 2.2.2 现有算法比较和优缺点分析

目前，图同构性检测领域的主要算法包括VF算法、Nauty、Saucy等。VF算法是早期的代表，它通过回溯法逐步构造顶点的映射，但存在效率较低的缺点。Nauty算法则利用了图的“规范标签”概念，有效减少了搜索空间，是目前广泛应用的算法之一。

尽管Nauty在许多场景下表现良好，但面对某些特定类型的图（如稠密图），其性能仍有待提高。因此，针对不同的应用场景和图的特征，选择合适的图同构性检测算法至关重要。

**以下是本章的总结内容：**

- 图的基本概念和分类，包括无向图、有向图、简单图、多重图的定义和区别。
- 同构图的定义以及同构性质的判定方法。
- 算法复杂度与图规模的关系，并提出了对大规模图分析的可能性。
- 现有图同构性检测算法的比较，包括VF算法、Nauty和Saucy等，并分析了它们的优缺点。
- 对图同构性检测未来研究方向的展望，包括对于特定图类型和大数据环境下算法的优化与改进。

# 3. Python在图同构性检测中的应用实践

在现代计算机科学中，图论是研究图的数学理论和图模型的算法应用的基础学科。图同构性检测作为图论中的一个核心问题，其对于理解和比较不同图结构之间的关系具有重要的意义。Python作为一种广泛应用于数据科学、网络分析和算法实现的语言，其在图同构性检测的实践应用中也表现出强大的能力。本章节将深入探讨Python在图同构性检测中的应用，包括Python图论库的介绍、图同构性检测算法的实现以及性能测试和优化策略。

## 3.1 Python图论库的介绍和应用

图论库为图同构性检测提供了强大的工具支持，Python社区提供了多个功能丰富的图论库，其中NetworkX是最著名的图处理库之一。接下来，将详细介绍NetworkX库的安装、基本操作以及使用NetworkX进行图的构建和分析。

### 3.1.1 NetworkX库的安装和基本操作

NetworkX是一个用Python编写的软件包，它提供了生成图、操作图以及计算图的各种属性等功能。安装NetworkX非常简单，可以直接通过pip进行安装：

pip install networkx

安装完成后，我们可以通过简单的代码示例来展示如何创建一个图，并进行基本操作：

import networkx as nx

# 创建一个空的有向图
G = nx.DiGraph()

# 添加节点和边
G.add_node(1)
G.add_edge(1, 2)
G.add_edge(1, 3)

# 输出图中的所有节点和边
print(G.nodes())  # 输出: [1]
print(G.edges())  # 输出: [(1, 2), (1, 3)]

在NetworkX中，还可以方便地绘制图形，以便于直观地理解图的结构：

import matplotlib.pyplot as plt

# 绘制图
nx.draw(G, with_labels=True)
plt.show()

上面的代码将生成一个简单的有向图，并使用matplotlib进行可视化展示。

### 3.1.2 使用NetworkX进行图的构建和分析

NetworkX库不仅提供了创建和绘制图的功能，还提供了丰富的图分析工具。例如，计算图的中心性（centrality）可以用来识别图中的关键节点：

# 计算并输出节点的度中心性
centrality = nx.degree_centrality(G)
print(centrality)

对于