【最小生成树算法】：Python中的图结构优化关键

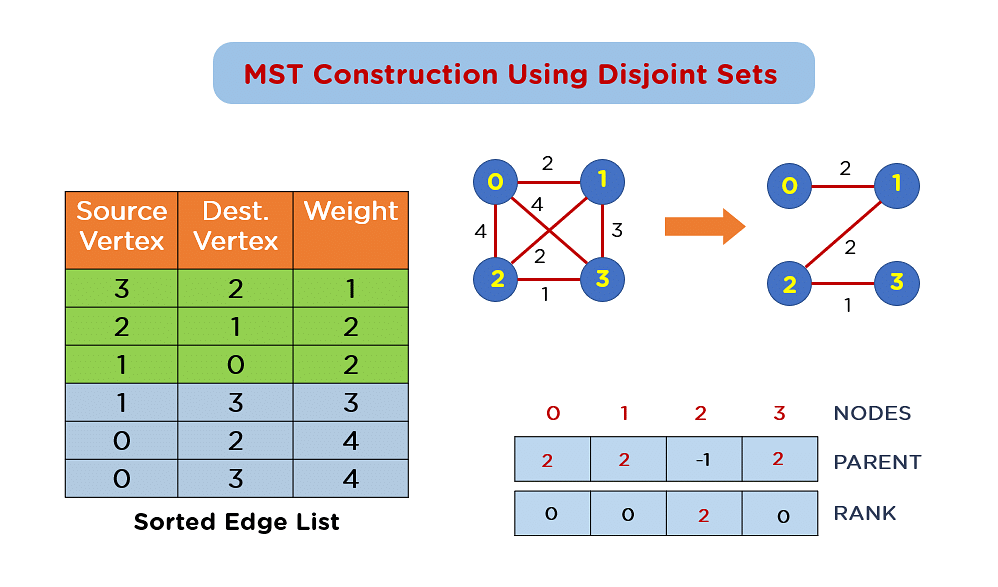
# 1. 最小生成树算法的基本概念

在探索网络设计、电路板布局或其他需要将节点连接以最小化成本问题时，最小生成树算法（MST）提供了解决方案。这种算法可以追溯到19世纪，由数学家首次提出，用于解决几何问题，但现在它已经成为图论的核心组成部分。简而言之，最小生成树是指在一个加权连通图中找到的、包含所有顶点且边的总权重最小的树形结构。在下一章中，我们将深入探讨图结构和树理论，从而更好地理解最小生成树算法的背景。

# 2. 图结构与树理论

## 2.1 图论基础与图的类型

### 2.1.1 无向图和有向图的定义

在图论中，图是由节点（或顶点）以及连接这些节点的边组成的一种数据结构。无向图是图的一种类型，在无向图中，边没有方向，即边是双向的，它连接着一对节点。例如，如果节点A和节点B之间有一条无向边，则表示节点A和节点B是相互连接的。

有向图则不同，它包含有方向的边，即每条边都指定了一个方向，由一个起点指向一个终点。在有向图中，如果从节点A到节点B有一条有向边，那么我们可以说存在一条从A指向B的边，但不意味着存在一条从B指向A的边。

### 2.1.2 图的表示方法：邻接矩阵与邻接表

图的表示方法主要有邻接矩阵和邻接表。

**邻接矩阵**是一种表示图中所有边关系的二维矩阵，对于有n个节点的图来说，它的邻接矩阵是一个n×n的矩阵。如果节点i和节点j之间有边连接，那么矩阵中相应的元素为1（或边的权重），否则为0。邻接矩阵适用于表示稠密图，并且便于实现图的查询操作。

# 无向图的邻接矩阵表示示例
import numpy as np

# 初始化邻接矩阵，0表示没有边，1表示有边
adjacency_matrix = np.array([[0, 1, 1, 0],
                             [1, 0, 1, 1],
                             [1, 1, 0, 0],
                             [0, 1, 0, 0]])

print(adjacency_matrix)

**邻接表**是另一种图的表示方式，它用一个数组存储所有顶点，每个顶点有一个链表与其相连，链表中包含所有与该顶点直接相连的顶点。在邻接表中，边的表示不像邻接矩阵那样是固定的数组位置，而是以链表的形式出现。邻接表通常用于表示稀疏图，并且能够节省空间，特别是当图中边的数量远小于可能的最大数量时。

# 无向图的邻接表表示示例
adjacency_list = {
    0: [1, 2],
    1: [0, 2, 3],
    2: [0, 1],
    3: [1]
}

for vertex, edges in adjacency_list.items():
    print(f"Vertex {vertex} is connected to: {edges}")

在选择图的表示方法时，需要考虑到图的特性（如是否稀疏或稠密），以及操作需求（比如边的查找频率）。

## 2.2 树和最小生成树的定义

### 2.2.1 树的概念与性质

树是一种特殊的图，它由节点和边组成，且没有环。树中的边数总是比节点数少一个。树具有以下基本性质：

- 树中的任意两个顶点之间有且仅有一条路径；
- 树是无环的；
- 在有n个节点的树中，有n-1条边。

树的结构可以定义为由一个根节点开始，向下延伸至任意深度，每个节点可以有零个或多个子节点，但所有节点间没有循环。

### 2.2.2 最小生成树的数学模型

最小生成树（Minimum Spanning Tree，MST）是图论中的一个概念，特指在一个加权无向图中找到一个边的子集，这个子集构成的树包含图中的所有顶点，并且边的总权重最小。这里加权指的是每条边有一个权重值，我们希望总权重最小。

数学模型可以描述为：给定一个带权连通无向图G=(V,E)，其中V表示顶点的集合，E表示边的集合，每条边都有一个权重。最小生成树是一个子图G'=(V, E')，其中E'是E的一个子集，包含的边数为|V|-1（即恰好构成树的条件），并且这些边的权重和最小。

## 2.3 算法理论基础

### 2.3.1 时间复杂度和空间复杂度分析

算法的时间复杂度是指执行算法所需要的计算工作量，通常用大O符号表示，比如O(n)表示算法的运行时间与数据规模n成线性关系。空间复杂度是指算法在运行过程中临时占用存储空间的大小，同样用大O符号表示。

在评估最小生成树算法时，我们会关注算法的时间复杂度和空间复杂度，因为它们直接影响算法的性能和适用范围。例如，Kruskal算法的时间复杂度可以通过使用并查集数据结构优化至接近O(ElogE)，而Prim算法则可以通过优先队列优化至O(ElogV)。空间复杂度通常与存储图的结构和算法使用的辅助数据结构有关，对于最小生成树算法来说，空间复杂度主要和边的数量E和顶点的数量V有关。

### 2.3.2 算法的正确性和效率

算法的正确性是指算法实现能够正确完成预期的任务。在最小生成树算法中，正确性意味着算法能够确保最终输出的是一棵包含所有顶点，边的总权重最小的树。

算法的效率则包含了算法的时间效率和空间效率。时间效率通常用时间复杂度来衡量，空间效率则用空间复杂度来衡量。效率高的算法能够在较短时间内用较少的空间资源完成计算。对于最小生成树算法来说，效率的一个关键指标就是边的处理速度，因为边的数量往往决定了算法的运行时间。

为了提高效率，算法设计中常会引入各种优化策略，如使用有效的数据结构（如并查集、优先队列）和算法（如贪心策略），来减少不必要的计算和存储，从而达到优化整体性能的目的。

# 3. 最小生成树算法的实现与应用

## 3.1 Kruskal算法的原理与实践

Kruskal算法是一种用于寻找最小生成树的贪心算法。其核心思想是按照边的权重顺序将边加入生成树中，同时确保加入的边不会与已经加入的边形成环路。

### 3.1.1 Kruskal算法步骤详解

算法步骤如下：

1. 将所有边按权重从小到大排序。
2. 初始化一个森林，其中每个顶点自成一个连通分量。
3. 从排序后的边列表中依次取出最小的边，检查加入这条边是否会形成环路。
4. 如果加入这条边不会形成环路，则将其加入最小生成树中，并合并相关的连通分量。
5. 重复步骤3和4直到最小生成树中包含了所有顶点。

### 3.1.2 实际编程中的优化技巧

在编程实践中，以下技巧可以优化Kruskal算法的性能：

- 使用数据结构如并查集（Disjoint-set Union，DSU）来高效地检测环路。
- 对边进行排序时，可以采用如归并排序、堆排序等高效的排序算法来减少时间复杂度。
- 在合并连通分量时，需要平衡数据结构来快速访问并更新父节点，以优化路径压缩。

下面是一个使用并查集和Python的示例代码：

class DisjointSetUnion:
    def __init__(self, n):
        self.parent = [i for i in range(n)]
        self.rank = [0] * n
    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]
    def union(self, x, y):
        rootX = self.find(x)
        rootY = self.find(y)
        if rootX == rootY:
            return False
        if self.rank[rootX] > self.rank[rootY]:
            self.