【广度优先搜索】：Python BFS算法详解与实践

# 1. 广度优先搜索（BFS）算法概述

广度优先搜索（BFS）算法是一种用于图遍历或搜索树结构的算法，它从根节点开始，逐层扩展直到所有节点都被访问。BFS适用于无权图，以确保找到最短路径。它以一种系统且平滑的方式遍历所有节点，通常借助队列来实现。作为基础算法，BFS是理解和构建更复杂算法的基石，在网络路由、社交网络分析、路径规划等多个领域有广泛应用。接下来我们将深入探讨其理论基础以及如何在Python中实现BFS算法。

# 2. BFS算法的理论基础

## 2.1 图论简介

### 2.1.1 图的基本概念

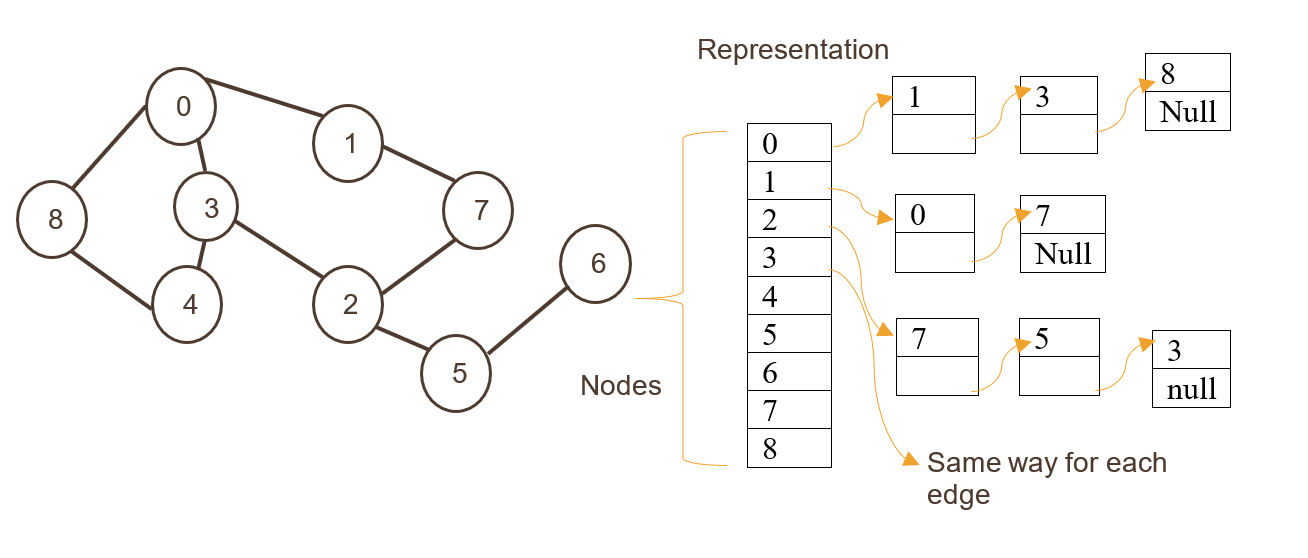
图是由顶点（Vertex）和边（Edge）组成的数学结构，用来抽象和表示实体间的关系。在图中，顶点通常用来表示实体，边用来表示实体间的关系或连接。图可以是有向的，也可以是无向的。有向图中，边具有方向，从一个顶点指向另一个顶点；无向图中，边是双向的，连接两个顶点但不具有方向。

图论中的关键概念还包括路径（Path），它是由顶点和边组成的序列，其中每个顶点和边在序列中出现一次。若路径的开始顶点和结束顶点相同，则称为环（Cycle）。

### 2.1.2 图的分类及特性

图可以根据其属性分为多种类型，主要有：
- 简单图（Simple Graph）：没有自环和平行边的图。
- 加权图（Weighted Graph）：边有与之相关的权重或成本。
- 完全图（Complete Graph）：图中的每对不同的顶点之间都存在一条边。
- 二分图（Bipartite Graph）：图的顶点可以分为两个不相交的集合，图中每条边的两个端点分别属于这两个不同的集合。

图的特性包括但不限于：
- 连通性：无向图中任意两个顶点都是连通的，即存在路径相连。
- 强连通性：有向图中任意两个顶点都是相互可达的，即存在有向路径。
- 周长：图中所有顶点的最短路径之和。
- 直径：图中任意两个顶点之间最长最短路径的长度。

## 2.2 BFS算法原理

### 2.2.1 搜索过程描述

BFS（广度优先搜索）是一种用于图的遍历或搜索树结构的算法，它从根节点开始，逐层向外扩展。其核心思想是优先探索与当前节点距离较近的邻接节点，即“一层层”搜索。算法使用队列来维护待访问的节点，遵循先进先出（FIFO）的原则。

BFS搜索过程中，初始时将起始顶点加入队列，接着开始循环，直到队列为空为止。在每次循环中，从队列中取出一个顶点，对其进行处理，然后将该顶点的所有未访问的邻接顶点加入队列中等待下一轮处理。这样的过程确保了算法能够最先访问到距离起始顶点最近的顶点。

### 2.2.2 时间复杂度分析

BFS算法的时间复杂度取决于图的表示方法以及边的遍历方式。以邻接表表示图为例，假设图中有V个顶点和E条边，算法的时间复杂度如下：

- 对每个顶点进行一次访问，时间复杂度为O(V)。
- 对每条边进行一次检查，时间复杂度为O(E)。

综合考虑，BFS的时间复杂度为O(V+E)。这意味着算法的执行时间与图中的顶点数和边数成线性关系。

## 2.3 BFS与其它搜索算法比较

### 2.3.1 BFS与深度优先搜索（DFS）对比

BFS和DFS是两种常用的图遍历算法，它们在策略上有所不同：

- **BFS**是一种逐层遍历的策略，从起始点开始，先访问所有距离为1的顶点，然后是距离为2的顶点，依此类推。这种方式可以快速找到从起始点到目标顶点的最短路径。
- **DFS**则采用深度优先的策略，从起始点开始，沿着一条路径一直深入，直到无法继续为止，然后回溯到上一个分叉点选择其他路径继续搜索。DFS在处理有大量节点和边的图时，空间消耗较BFS小，但不保证能找到最短路径。

选择BFS还是DFS通常取决于具体问题的需求。如果需要找到最短路径，BFS通常是更好的选择。

### 2.3.2 BFS在不同问题中的应用选择

BFS算法在很多场景下有其独特的应用，例如：

- **迷宫问题**：通过BFS可以找到从起点到终点的最短路径。
- **网络爬虫**：为了尽可能均匀地遍历网页，BFS可以帮助爬虫设计合理的访问策略。
- **社交网络分析**：在社交网络中，BFS可以用于找到好友关系中的最近共同好友。

在选择使用BFS或DFS时，需要考虑目标、图的结构特性、内存限制等因素，以便于更高效地解决问题。

以上内容详细介绍了BFS算法的理论基础，包括图论的基本概念、分类、特性以及BFS算法的原理和时间复杂度。同时，与深度优先搜索（DFS）进行了比较，明确了各自的优势和应用场景。这些理论知识为接下来的算法实现和应用案例分析奠定了基础。

# 3. Python BFS算法的实现

## 3.1 Python环境准备与基础知识

### 3.1.1 Python的安装与配置

在开始编写Python代码实现BFS算法之前，我们需要确保有一个适合的开发环境。Python是一种解释型语言，这意味着它可以在多种操作系统上运行，并且用户界面友好。要安装Python，请按照以下步骤操作：

1. 访问Python官方网站（***）下载适合您操作系统的最新版本。
2. 运行下载的安装程序。在安装过程中，请确保勾选“Add Python to PATH”选项，这样可以在命令行中直接运行Python。
3. 安装完成后，打开命令提示符或终端，并输入`python --version`以验证Python是否正确安装。如果您看到Python版本号的输出，说明安装成功。

### 3.1.2 Python基础语法回顾

Python的基础语法简单明了，非常适合快速上手编程。下面是一些编写BFS算法时会用到的基础概念：

- **变量**: 用于存储数据值。Python是动态类型语言，无需声明变量类型。

  x = 10       # 整数赋值
  y = "hello"  # 字符串赋值

- **列表**: 用于存储序列类型的数据。

  my_list = [1, 2, 3, 4, 5]  # 整数列表
  names = ["Alice", "Bob", "Charlie"]  # 字符串列表

- **循环**: `for`和`while`循环用于重复执行代码块。

  for i in range(5):  # for循环遍历数字0到4
      print(i)
  i = 0
  while i < 5:  # while循环同样遍历数字0到4
      print(i)
      i += 1

- **条件语句**: `if`语句用于执行基于条件的代码块。

  if age > 18:
      print("You are an adult.")
  elif age > 12:
      print("You are a teenager.")
  else:
      print("You are a child.")

- **函数**: 用于封装代码块，使得它们可以被多次调用。

  def greet(name):
      return "Hello, " + name + "!"

  print(greet("Alice"))  # 输出: Hello, Alice!

- **数据结构**: 如字典和集合等，用于组织和处理数据。

  my_dict = {"name": "Alice", "age": 25}  # 字典用于存储键值对
  my_set = {1, 2, 3}  # 集合用于存储唯一值

为了实现BFS算法，我们将主要使用列表来维护待访问节点，并使用字典来表示图结构。理解这些基础知识对于后续的算法实现至关重要。

## 3.2 Python中BFS算法的代码实现

### 3.2.1 标准BFS算法的Python代码

让我们从一个基本的BFS算法实现开始，下面的代码展示了如何使用Python来实现BFS遍历一个简单的无向图。

from collections import deque

# 创建图并用邻接列表表示
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

# 实现BFS算法
def bfs(graph, start):
    visited = set()  # 用于记录已访问的节点
    queue = deque([start])  # 队列用于存放待访问的节点

    while queue:
        vertex = queue.popleft()  # 取出队列的元素
        if vertex not in visited:
            visited.add(vertex)  # 标记为已访问
            print(vertex, end=' ')  # 打印节点，也可以是其他处理
            # 将当前节点的邻居加入队列
            for neighbour in graph[vertex]:
                if neighbour not in visited:
                    queue.append(neighbour)

# 调用函数开始遍历
bfs(graph, 'A')

在上述代码中，我们首先导入了`deque`类，它是一个双端队列，适合用作BFS算法中的队列数据结构，因为可以在两端分别进行添加和删除操作。

通过调用`bfs(graph, 'A')`函数，算法将从节点`'A'`开始访问所有可达节点。首先将起始节点`'A'`放入队列中，并将其标记为已访问。接着，不断从队列中取出节点，并将其邻居加入队列中（前提是这些邻居尚未被访问过）。如此循环，直至队列为空，这意味着所有节点都被访问过。

### 3.2.2 利用队列优化BFS性能

队列是实现BFS算法的关键数据结构，它帮助我们保持了节点的访问顺序。