**中的数据保护：加密与安全存储秘籍，数据安全无小事

# 1. 数据保护与加密基础

随着数字化时代的到来，数据已成为企业与个人的关键资产。然而，数据泄露、滥用及安全威胁不断攀升，数据保护与加密技术的重要性日益凸显。本章节旨在为读者介绍数据保护与加密技术的基础知识，为后续更深入探讨加密算法、数据存储安全、隐私法规及合规性等方面打下坚实的理论基础。

## 1.1 数据保护的重要性

数据保护的首要目的是确保信息资产的安全，防止数据泄露、篡改和丢失。对于企业而言，数据泄露不仅会带来经济损失，更会对品牌信誉造成严重打击。对于个人而言，个人隐私信息的泄露可能会导致财产安全和人身安全风险。因此，采取有效的数据保护措施是现代IT从业者必须面对的关键挑战之一。

## 1.2 加密的作用与类型

加密是一种将数据转换为只有特定方才能解读的格式的技术。基本原理是通过算法对数据进行编码，即使数据被未授权的第三方截获，也无法理解其真实含义。根据密钥的使用方式和数量，加密技术主要分为两大类：对称加密和非对称加密。

### 1.2.1 对称加密

在对称加密中，加密和解密过程使用同一个密钥。这种方式的加密速度快，但密钥的安全分发与管理成为一大挑战。常见的对称加密算法包括高级加密标准（AES）和数据加密标准（DES）等。

### 1.2.2 非对称加密

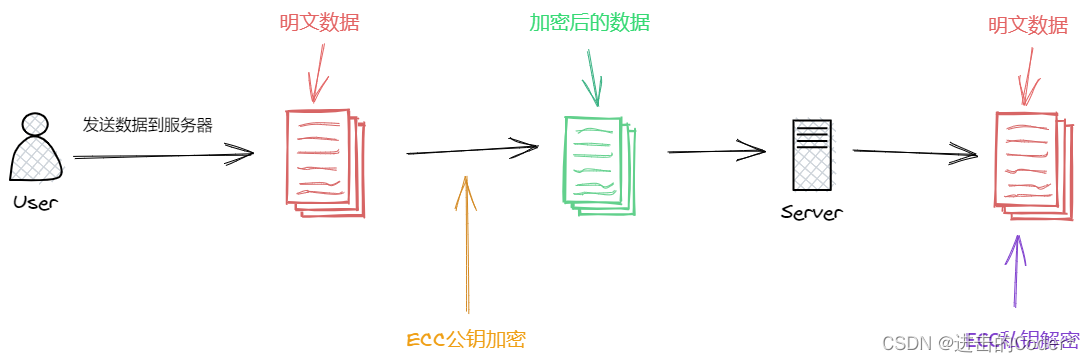
非对称加密使用一对密钥：公钥和私钥。公钥可以公开分享，用于加密数据；私钥必须保密，用于解密。RSA和椭圆曲线加密（ECC）算法是两种常用的非对称加密技术。

理解了对称与非对称加密的基础知识之后，接下来我们将详细探讨这些加密技术的工作原理及实践应用。

# 2. 加密技术的理论与实践

### 2.1 对称加密算法

#### 2.1.1 对称加密的基本概念

对称加密，顾名思义，是在加密和解密过程中使用相同密钥的加密方式。这是最古老和最快速的加密形式，因为加密和解密过程使用了相同的算法。该算法的安全性依赖于密钥的保密性，一旦密钥被泄露，加密数据的安全性也就无从谈起。

对称加密涉及的基本操作包括：明文、密钥、加密算法和密文。明文是原始数据，密钥是加密和解密过程的秘密参数，加密算法是将明文转换为密文的数学函数，而密文是通过加密算法处理后得到的不可理解的文本。

在实际应用中，常见的对称加密算法有AES、DES、3DES等。每种算法都有其特定的密钥长度、加密模式和工作原理。

#### 2.1.2 常用对称加密算法对比

在众多对称加密算法中，AES（Advanced Encryption Standard）是最为广泛使用和推荐的算法之一。AES支持128、192和256位的密钥长度，提供了较高的安全性，并且速度较快，适合用于加密大量数据。

DES（Data Encryption Standard）是一种较早的加密标准，由于其56位的密钥长度已不再安全，现在已被AES所取代。而3DES（Triple DES）是对DES的加强，通过使用三个56位的密钥对数据进行三次加密，但其效率较低，也逐渐被AES替代。

### 2.2 非对称加密算法

#### 2.2.1 非对称加密的基本概念

与对称加密相对的是非对称加密，它使用一对密钥——公钥和私钥。公钥可以公开，用于加密数据，而私钥必须保密，用于解密。非对称加密的这种特性使其在互联网通信中非常有用，尤其是用于数字证书和SSL/TLS协议。

非对称加密算法的核心在于密钥对的生成机制，以及数学上的单向函数。公钥和私钥是通过数学算法生成的，确保了数据的单向加密和解密。常见的非对称加密算法包括RSA、ECC（Elliptic Curve Cryptography）、DH（Diffie-Hellman）等。

#### 2.2.2 RSA算法原理及实践

RSA算法是目前最流行的非对称加密算法之一，它由Rivest、Shamir和Adleman在1977年提出。RSA算法的安全性基于大数分解的困难性，即给定两个大质数，要分解出它们的乘积是极其困难的。

RSA加密使用公钥（由模数n和指数e组成）进行加密，而私钥（由模数n和指数d组成）用于解密。在实际应用中，生成密钥对可以通过专门的工具或编程语言提供的库函数。例如，使用Python语言的`cryptography`库可以很容易地生成RSA密钥对：

from cryptography.hazmat.backends import default_backend
from cryptography.hazmat.primitives.asymmetric import rsa

# 生成私钥
private_key = rsa.generate_private_key(
    public_exponent=65537,
    key_size=2048,
    backend=default_backend()
)

# 获取公钥
public_key = private_key.public_key()

# 保存密钥到文件
with open("private_key.pem", "wb") as f:
    f.write(private_key.private_bytes(
        encoding=serialization.Encoding.PEM,
        format=serialization.PrivateFormat.PKCS8,
        encryption_algorithm=serialization.BestAvailableEncryption(b'mypassword')
    ))
with open("public_key.pem", "wb") as f:
    f.write(public_key.public_bytes(
        encoding=serialization.Encoding.PEM,
        format=serialization.PublicFormat.SubjectPublicKeyInfo
    ))

#### 2.2.3 ECC算法原理及实践

ECC是另一种非对称加密算法，它基于椭圆曲线上的点群运算。相较于RSA算法，ECC可以在使用更短的密钥长度的同时，提供相当甚至更高的安全性。由于其密钥长度短，ECC在移动设备和智能卡等资源受限的环境中特别受欢迎。

ECC加密同样涉及到密钥对的生成。下面是一个简单的Python代码示例，展示了如何使用`cryptography`库生成ECC密钥对：

from cryptography.hazmat.backends import default_backend
from cryptography.hazmat.primitives.asymmetric import ec

# 生成私钥
private_key = ec.generate_private_key(
    curve=ec.SECP256R1(),
    backend=default_backend()
)

# 获取公钥
public_key = private_key.public_key()

# 保存密钥到文件
with open("private_key.pem", "wb") as f:
    f.write(private_key.private_bytes(
        encoding=serialization.Encoding.PEM,
        format=serialization.PrivateFormat.PKCS8,
        encryption_algorithm=serialization.BestAvailableEncryption(b'mypassword')
    ))
with open("public_key.pem", "wb") as f:
    f.write(public_key.public_bytes(
        encoding=serialization.Encoding.PEM,
        format=serialization.PublicFormat.SubjectPublicKeyInfo
    ))

### 2.3 哈希函数与数字签名

#### 2.3.1 哈希函数的工作原理

哈希函数是一种单向加密算法，可以将任意长度的数据映射到固定长度的哈希值。哈希函数有三个特点：单向性、快速性、抗碰撞性。单向性指的是，从哈希值几乎不可能计算出原始数据；快速性指的是对数据进行哈希计算非常迅速；抗碰撞性指的是找到两个不同的数据，使得它们的哈希值相同，是非常困难的。

常见的哈希函数包括MD5、SHA-1、SHA-2和SHA-3系列。MD5和SHA-1由于安全漏洞，现在已经不再推荐使用。SHA-2和SHA-3系列提供了更高的安全性，并被广泛应用于密码学和数据完整性验证中。

#### 2.3.2 数字签名的创建和验证过程

数字签名是使用非对称加密技术创建的一种电子签名，它用于验证信息的完整性和来源的真实性。数字签名的创建通常涉及到哈希函数和非对称加密技术的结合。

创建数字签名的过程包括以下步骤：
1. 使用哈希函数对原始消息进行哈希计算，得到固定长度的哈希值。
2. 使用签名者的私钥对哈希值进行加密，生成数字签名。
3. 将数字签名附加到原始消息上，一起发送给接收者。

接收者收到消息和数字签名后，会执行以