【随机森林实战攻略】：进阶决策树技术，图表与分析技巧

# 1. 随机森林算法概述

随机森林算法是机器学习中一种广泛应用的集成学习技术，它基于构建多个决策树并结合它们的预测来提升整体模型的准确性和泛化能力。它由Breiman在2001年提出，旨在解决决策树的过拟合问题，同时提升模型在新数据上的表现。

## 1.1 算法的发展背景

随机森林是在传统决策树模型的基础上发展而来。决策树简单直观，但容易过拟合，即在训练数据上表现出色，但在未见数据上表现不佳。随机森林通过引入随机性，让模型在预测时能够更加稳健，有效避免过拟合。

## 1.2 算法的主要思想

随机森林的核心思想是“森林”中每棵树都是独立生成的，并且每棵树在预测时只考虑部分特征，使得每棵树都是“偏颇”的。这种“有偏”方法在结合时，却能显示出良好的整体性能。

## 1.3 算法的应用场景

随机森林适用于分类和回归任务，尤其在大数据环境下，由于其高效并行的计算方式和对缺失数据的鲁棒性，使其在生物信息学、金融分析、图像识别等领域广泛应用。

随机森林算法的这些特点和优势，将在接下来的章节中进行深入探讨。

# 2. 随机森林的理论基础

随机森林是一种集成学习方法，主要依赖于构建多个决策树并结合它们的预测来进行最终的决策。理解随机森林的理论基础不仅需要掌握决策树的相关知识，还包括理解集成学习的原理以及如何通过关键参数影响模型的性能。

### 2.1 决策树的基本概念与原理

决策树是随机森林的基本构成单位，也是机器学习中重要的分类与回归算法。它模拟了人类的决策思维，通过一系列的决策规则对数据进行分类或回归。

#### 2.1.1 决策树的构建过程

构建决策树通常包括三个步骤：特征选择、决策树生成和剪枝。以下是详细的构建过程：

1. **选择最佳分裂特征**：在每个节点，算法会计算所有可能特征和分裂点，并选择能带来最大信息增益（分类任务）或信息增益率（回归任务）的特征和分裂点作为最佳分裂依据。

2. **分裂节点**：根据选定的最佳特征和分裂点将节点划分为子节点，每个子节点代表了基于特征值的规则。

3. **终止条件**：递归地重复上述步骤，直到满足终止条件。终止条件通常包括节点中的样本数量小于一个阈值或节点内所有样本的标签相同。

4. **决策树剪枝**：为了防止过拟合，需要对决策树进行剪枝。剪枝的方法可以是预剪枝（在生成树时就限制树的大小）或后剪枝（先生成一棵完整的树，然后移除一些子树）。

在构建决策树时，一个重要的算法是ID3（Iterative Dichotomiser 3），它采用信息增益作为分裂标准；C4.5是ID3的改进版本，使用信息增益率避免偏向于取值较多的特征；CART（Classification and Regression Trees）则是另一种流行的决策树算法，支持分类和回归任务。

#### 2.1.2 决策树的剪枝策略

剪枝策略能够有效减少过拟合，提高模型的泛化能力。常用的剪枝方法有：

- **预剪枝**：在树的构建过程中就设定停止条件，例如设定最大树深度、最小样本数、最大叶子节点数等。

- **后剪枝**：先生成完整的树，再从叶子节点开始考虑剪枝。剪枝操作会评估移除子树对模型性能的影响，并选择性能下降最小的子树进行移除。

剪枝后，需要使用验证集测试决策树的性能，以确定是否需要进一步剪枝或停止剪枝。

### 2.2 随机森林的理论模型

随机森林通过结合多个决策树来进行预测，从而提升模型的准确性并降低过拟合的风险。

#### 2.2.1 随机森林的集成学习方法

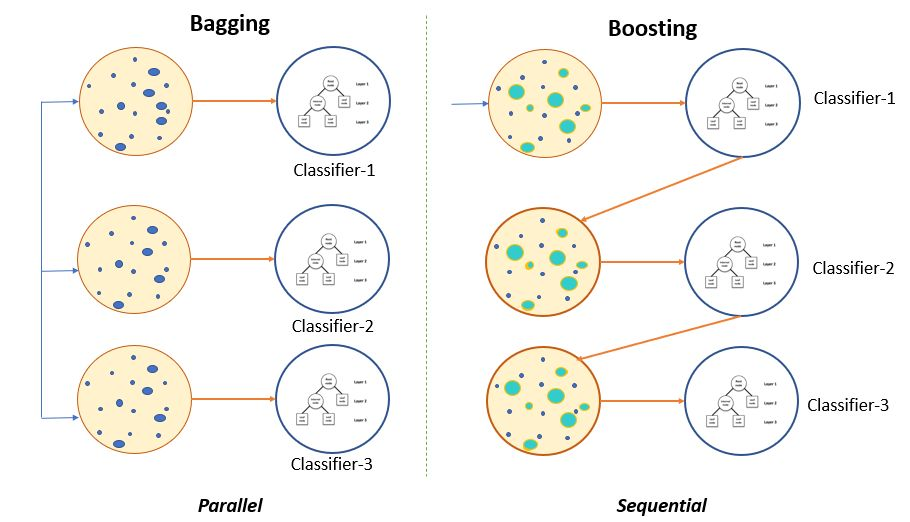
随机森林是一个典型的Bagging（自举汇聚法）模型，它在每次分裂节点时只从训练集的全部特征中随机抽取固定数量的特征子集。这种随机性使得森林中的每棵树都各不相同，从而增加模型的多样性。

构建随机森林的基本步骤如下：

1. **初始化森林大小N**：确定森林中决策树的数量N。

2. **训练每棵决策树**：对每个树重复以下步骤：
- 从原始数据集中随机抽取N个样本（有放回的抽样）形成新的训练集。
- 从全部特征中随机抽取m个特征（m远小于全部特征数），并利用这些特征来构建单个决策树。
- 当树达到设定的最大深度、最小分裂样本数或达到其他终止条件时停止树的生长。

3. **聚合预测结果**：对分类任务，随机森林的预测结果是多棵树投票的结果；对回归任务，则是多棵树预测值的平均。

#### 2.2.2 随机森林与偏差-方差权衡

随机森林作为一种集成方法，在提高模型准确性的同时也涉及到偏差-方差权衡问题。偏差-方差权衡是指模型的泛化误差可以分解为偏差、方差和不可约误差三个部分。随机森林通过增加模型的多样性来减少方差，从而在一定程度上降低过拟合的风险。

- **偏差**：模型对训练数据的预测平均值与真实值之间的差异。集成模型如随机森林，由于其决策树的生成依赖于随机过程，单棵树可能具有较高的偏差。
- **方差**：模型预测结果的波动性，即不同训练集上模型预测值的差异。随机森林通过构建多个决策树来降低整体模型的方差，提高泛化能力。

通过调整随机森林中的树的数量和特征抽样数量等参数，可以在这个偏差和方差之间寻找最佳平衡点，从而得到最佳的模型性能。

### 2.3 随机森林的关键参数

随机森林模型中的关键参数对模型性能有显著的影响，合理选择和调整这些参数是模型优化的重要环节。

#### 2.3.1 树的数量和深度对性能的影响

- **树的数量**：更多的树可以提高模型的稳定性和准确性，但也会导致计算复杂度的增加。一般而言，随着树的数量增加，随机森林的性能会逐步提升，直至达到一个稳定点。

- **树的深度**：树的深度决定了树的复杂度。较大的深度可能会导致过拟合，而较浅的树可能会导致欠拟合。理想的树深度应当在两者之间找到一个平衡，使得模型在保持泛化能力的同时也能很好地捕捉数据的特征。

#### 2.3.2 特征抽样和袋外误差估计

- **特征抽样**：在构建每棵树时，随机森林不是利用所有特征来进行分裂，而是从全部特征中随机选择m个特征（m < M，M为特征总数）。这一步骤增加了模型的随机性和多样性，但太小的m可能会导致模型性能下降。

- **袋外误差（Out-of-Bag Error）**：袋外误差是指对于随机森林中每棵树的训练样本，那些没有被该树使用的样本被称为袋外样本（OOB）。袋外误差就是每棵树的袋外样本误差的平均值，它可用于评估模型的泛化能力，而无需额外的验证集。

随机森林的关键参数需要在模型训练之前仔细调整，通常采用交叉验证等方法进行参数搜索和模型评估。下面通过示例代码展示如何使用随机森林算法，并详细解析关键代码块。

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split

# 加载数据集（这里用伪代码表示）
X, y = load_data()

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 初始化随机森林分类器
rf_clf = RandomForestClassifier(n_estimators=100, max_depth=5, random_state=42)

# 训练模型
rf_clf.fit(X_train, y_train)

# 使用模型进行预测
predictions = rf_clf.predict(X_test)

# 计算袋外误差
oob_error = 1 - rf_clf.oob_score_

print("袋外误差:", oob_error)

在上述代码中，`n_estimators` 参数代表了树的数量，`max_depth` 参数代表了树的最大深度。通过调整这些参数，可以实现对随机森林模型性能的优化。通过评估测试集上的准确性和袋外误差，可以评估模型的泛化能力和过拟合情况。在实际操作中，我们通常需要利用网格搜索（GridSearchCV）等方法来寻找最佳的参数组合。

# 3. 随机森林在数据分析中的应用

在数据分析的世界里，随机森林算法以其卓越的性能和稳健性，成为了机器学习领域中一颗耀眼的明珠。本章节将深入探讨随机森林在数据分析中的应用，包括数据预处理和特征工程、模型构建与调优，以及模型评估与验证等关键环节。

## 3.1 预处理和特征工程

在随机森林模型的训练和应用之前，数据的预处理和特征工程是不可或缺的步骤。这些步骤直接影响到模型的性能和最终的分析结果。

### 3.1.1 数据清洗与标准化

数据清洗是数据分析的第一步。在这一部分，我们将重点关注如何处理缺失值、异常值、重复数据以及数据类型转换等问题。

import pandas as pd
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler

# 加载数据集
data = pd.read_csv('data.csv')

# 处理缺失值
imputer = SimpleImputer(strategy='mean')
data_imputed = pd.DataFrame(imputer.fit_transform(data), columns=data.columns)

# 标准化数据
scaler = StandardScaler()
data_scaled = pd.DataFrame(scaler.fit_transform(data_imputed), columns=data.columns)

上述代码首先使用`SimpleImputer`类来填充缺失值，这里采用了平均值填充策略。接着，我们使用`StandardScaler`对数据进行标准化处理，使得每个特征的均值为0，标准差为1。

### 3.1.2 特征选择与降维技术

在数据预处理之后，特征选择和降维是另一个关键步骤。它能够减少数据维度，提高模型的计算效率和泛化能力。

from sklearn.feature_selection import SelectKBest, f_classif

# 假设data_scaled是已经标准化的数据
# 使用SelectKBest选择最佳的K个特征
selector = S