【主成分分析(PCA)的Python实现】：简化数据，3步抓住关键特征

# 1. 主成分分析(PCA)的基础概念

## 1.1 主成分分析的定义
主成分分析（Principal Component Analysis，简称PCA）是一种常用于统计分析和数据降维的方法。PCA的主要目标是从多个变量中提取出少数几个综合变量（主成分），这些主成分可以尽可能地代表原来的数据集。

## 1.2 PCA的基本原理
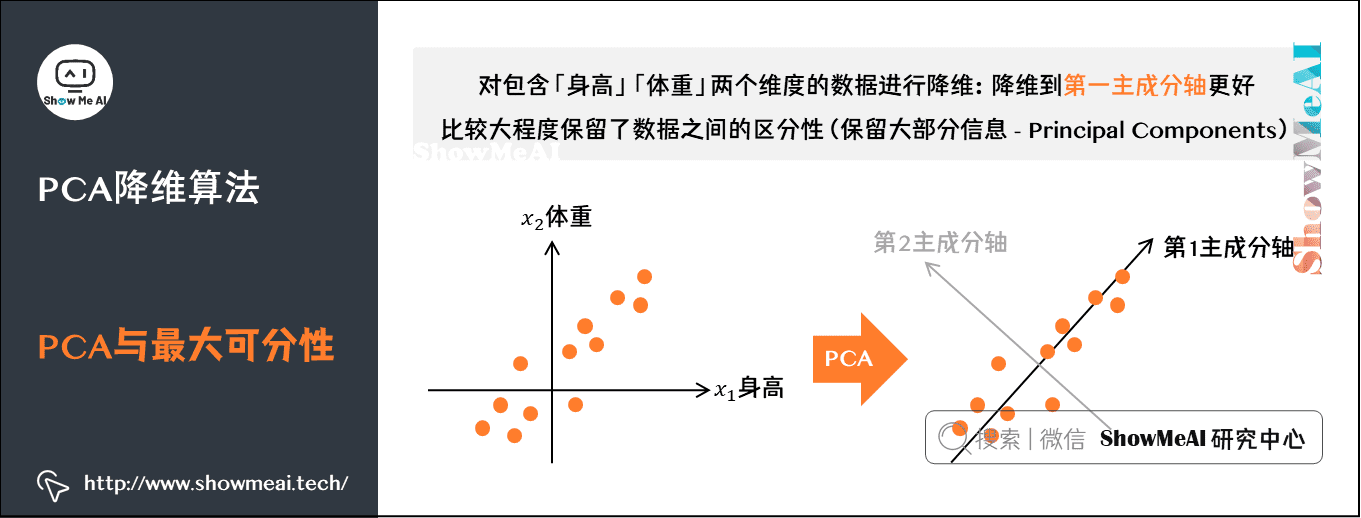
PCA的原理是基于数据集中的变量具有相关性的前提，通过正交变换将原始数据转换到一组线性不相关的变量，即主成分。这些主成分按照方差大小排序，方差最大的成分是第一主成分，以此类推。通过保留方差较大的主成分，可以在丢失尽可能少的信息的前提下，达到数据降维的目的。

## 1.3 PCA的应用场景
PCA广泛应用于数据科学和机器学习的多个领域，如特征提取、数据压缩、降噪等。在处理高维数据时，PCA能够有效地减少数据的维度，简化数据结构，使得数据分析和机器学习模型的训练变得更加高效和有效。

# 2. 主成分分析(PCA)的理论基础

### 2.1 主成分分析的目的和意义

#### 2.1.1 数据降维的必要性

在处理现实世界的高维数据时，我们常常会遇到“维度的诅咒”，它描述了数据维度增加导致计算量急剧增长，数据稀疏性增加，以及难以找到有意义的模式等现象。数据降维可以通过减少数据集中的特征数量，来降低计算复杂度，提高模型训练效率，同时避免过拟合，并且提升数据可视化的效果。

#### 2.1.2 主成分分析解决的问题

主成分分析（PCA）是一种统计技术，它利用正交变换将可能相关的变量转换为一组线性不相关的变量，这些新变量被称为主成分。PCA通过保留数据的主要变异，去除噪声和冗余，来解决以下几方面问题：

- **数据压缩**：通过降低维度，把高维数据压缩到较低维度，而不丢失过多信息。
- **模式识别**：降维后的数据更适合用于分类和聚类等模式识别任务。
- **可视化**：高维数据往往难以直观理解，PCA可以将数据投影到二维或三维空间进行可视化。

### 2.2 主成分分析数学原理

#### 2.2.1 方差和协方差的概念

PCA的核心是方差最大化。方差衡量数据分布的离散程度，协方差则描述了两个变量的线性关系。在PCA中，主成分由数据的协方差矩阵定义，主成分的方向对应于协方差矩阵的特征向量，而主成分的方差大小对应于特征值。特征值越大，其对应特征向量的方向上的数据点变化程度越大。

#### 2.2.2 特征值和特征向量的计算

计算特征值和特征向量是PCA过程中的一项重要步骤。特征值表示了特征向量方向上的数据变异程度。具体的数学过程如下：

- 设协方差矩阵为 \( \Sigma \)。
- 需要找到标量 \(\lambda\) 和非零向量 \(v\)，使得 \( \Sigma v = \lambda v \)。
- \(\lambda\) 就是特征值，对应的非零向量 \(v\) 是特征向量。

### 2.3 主成分分析的步骤

#### 2.3.1 数据标准化处理

数据标准化是PCA的第一步，因为PCA对数据的尺度很敏感。标准化处理使得每个特征维度对总方差的贡献相等，通常使用以下公式进行：

\[
x_{\text{standardized}} = \frac{x - \mu}{\sigma}
\]

这里 \(x\) 是原始数据，\(\mu\) 是均值，\(\sigma\) 是标准差。

#### 2.3.2 计算协方差矩阵

接下来，计算标准化后的数据的协方差矩阵。协方差矩阵是一个对称矩阵，其元素由如下公式给出：

\[
\Sigma = \frac{1}{n-1} X^T X
\]

其中 \(X\) 是 \(n \times p\) 维的数据矩阵，\(n\) 是样本数量，\(p\) 是特征数量。

#### 2.3.3 求解特征值和特征向量

在获得协方差矩阵之后，下一步是求解协方差矩阵的特征值和特征向量。在Python中，我们可以使用NumPy库提供的 `np.linalg.eig` 函数来实现这一功能：

import numpy as np

cov_matrix = np.cov(data.T)
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)

这段代码首先使用 `np.cov` 计算数据矩阵的协方差矩阵，然后使用 `np.linalg.eig` 函数求解特征值和特征向量。

PCA的每一步都紧密相连，理解其背后的数学原理对掌握PCA的实际应用至关重要。下一章节将介绍如何在Python中实现PCA，并展示具体的代码实现过程。

# 3. Python实现主成分分析(PCA)

## 3.1 Python中的数据处理库

### 3.1.1 NumPy基础

NumPy是Python中用于科学计算的核心库，它提供了一个强大的N维数组对象ndarray。NumPy数组是进行数值计算的基础数据结构，因为其内部实现了高效的多维数组操作，所以在进行矩阵运算和PCA分析时，NumPy是不可或缺的工具。

在进行PCA之前，我们通常需要对数据集进行中心化处理，即将数据的均值转换为零。这一步骤可以通过NumPy轻松完成。以下是使用NumPy进行数据中心化的示例代码：

import numpy as np

# 假设data是一个二维数组，代表我们的数据集
data = np.array([[1, 2], [3, 4], [5, 6]])

# 计算均值
mean_values = data.mean(axis=0)

# 中心化数据
centered_data = data - mean_values

print("Centered Data:")
print(centered_data)

### 3.1.2 Pandas与数据预处理

Pandas是Python的另一个强大的数据分析库，提供了高级数据结构和操作工具。它使得数据清洗和准备过程变得非常容易和直观。Pandas中的DataFrame是一个二维的、表格型的数据结构，带有标签的轴，这使得它在处理表格数据时非常有用。

在实际应用PCA之前，可能需要进行数据清洗，比如处理缺失值、转换数据类型等。以下是使用Pandas进行基本数据预处理的示例代码：

import pandas as pd

# 创建一个简单的DataFrame
df = pd.DataFrame({
    'A': [1, 2, 3, 4],
    'B': [5, 6, 7, 8],
    'C': [9, 10, 11, 12]
})

# 显示原始数据
print("Original Data:")
print(df)

# 假设我们想要将列A的数据类型转换为字符串
df['A'] = df['A'].astype(str)

# 显示转换后的数据
print("\nData after transformation:")
print(df)

## 3.2 使用sklearn进行PCA操作

### 3.2.1 sklearnPCA库的安装和导入

Scikit-learn（简称sklearn）是一个开源的机器学习库，它基于NumPy、SciPy和matplotlib构建。sklearn提供了许多用于数据挖掘和数据分析的工具，其中就包括PCA模块。为了能够使用sklearn中的PCA功能，首先需要安装sklearn库。安装完成后，就可以导入PCA类来使用它进行主成分分析了。

以下是如何安装和导入sklearn库以及PCA类的示例代码：

# 安装scikit-learn库，如果已经安装可以跳过这一步
!pip install scikit-learn

from sklearn.decomposition import PCA

### 3.2.2 sklearnPCA类的基本使用方法

sklearnPCA类是sklearn中执行主成分分析的工具。