神经网络权值更新揭秘：深度解析反向传播算法原理

# 1. 神经网络的基本概念和架构

## 1.1 神经网络的定义
神经网络（Neural Network）是一种模仿人脑神经元网络的计算模型，由大量节点（或称“神经元”）相互连接构成。它能够通过学习大量数据自动提取特征，用于解决各种复杂问题，如图像识别、语音识别等。

## 1.2 神经网络的类型
根据网络结构和用途，神经网络主要分为以下几类：
- 前馈神经网络（Feedforward Neural Networks）
- 卷积神经网络（Convolutional Neural Networks, CNN）
- 循环神经网络（Recurrent Neural Networks, RNN）
- 生成对抗网络（Generative Adversarial Networks, GAN）

## 1.3 神经网络的基本架构
一个典型的神经网络包含输入层、隐藏层和输出层：
- 输入层（Input Layer）接收原始数据。
- 隐藏层（Hidden Layers）由多层构成，神经元之间的权重负责特征学习。
- 输出层（Output Layer）输出最终结果，如分类标签或预测值。

神经网络的每一层可以由不同数量的神经元组成，而每一层神经元的数量、连接方式和激活函数的选择将直接影响网络的性能。接下来的章节将详细介绍反向传播算法，它是神经网络训练中最核心的部分。

# 2. 反向传播算法的理论基础

## 2.1 神经网络的权值更新理论
### 2.1.1 权值更新的目标函数

在神经网络中，权值更新的目标是为了最小化网络输出与实际数据之间的误差。这个目标通常被定义为一个目标函数，也称为损失函数（Loss Function）。目标函数衡量了模型预测值和真实值之间的不一致程度。最常用的损失函数是均方误差（Mean Squared Error, MSE），它计算所有预测值与真实值之间差值的平方和的平均值。

目标函数可以表示为：
\[ E(w) = \frac{1}{2} \sum_{i}(y_i - t_i)^2 \]
其中，\( E(w) \) 是目标函数，\( w \) 表示网络中的权值，\( y_i \) 表示网络对第 \( i \) 个输入样本的预测输出，\( t_i \) 表示对应的实际目标值。

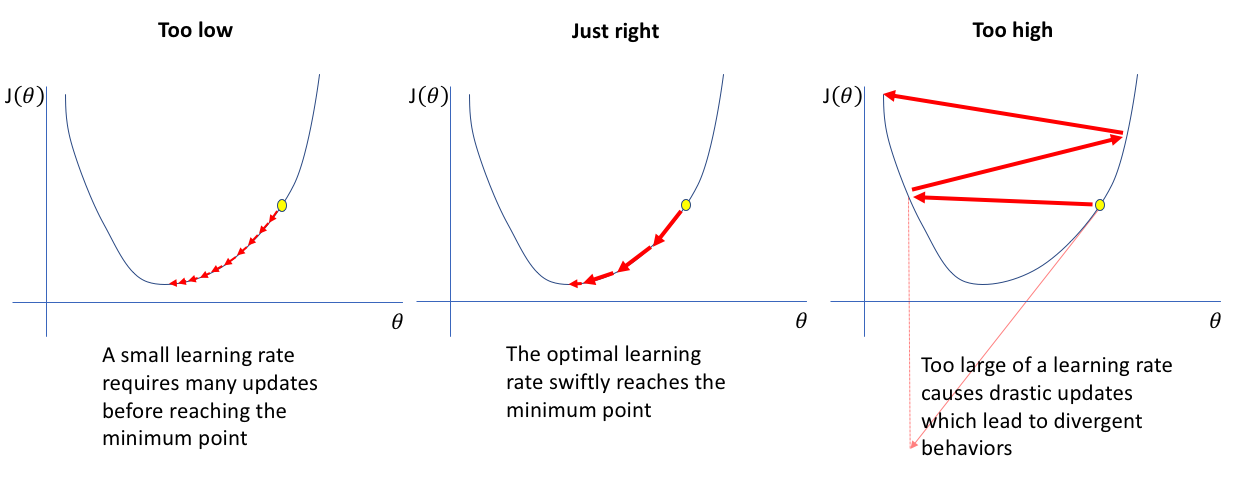
在实践中，我们通常使用梯度下降法来最小化目标函数。目标函数的梯度给出了权值调整的方向和大小，使得损失值下降最快。

### 2.1.2 误差函数的定义和性质

误差函数，或损失函数，是评估模型预测性能的关键。它为权值调整提供了数学上的方向。不同的任务和需求可能会采用不同的误差函数，例如分类任务常用交叉熵损失（Cross-Entropy Loss），回归任务通常使用均方误差。

误差函数具有以下性质：

- 连续性：误差函数在参数空间内是连续的，有利于使用基于梯度的方法进行优化。
- 可微性：误差函数是可微的，这样才能通过计算梯度来进行权值更新。
- 凸性：理想情况下，误差函数是凸的，这意味着局部最小值也是全局最小值，从而避免了局部最小的问题。但在实际应用中，很多神经网络的误差函数是高度非凸的，这可能导致算法在优化过程中陷入局部最小。

误差函数的最小化是通过迭代地调整网络中的权值来完成的。每次迭代中，我们根据误差函数关于每个权值的偏导数来调整权值，使得误差减小。

## 2.2 反向传播算法的数学推导

### 2.2.1 梯度下降法和链式法则

反向传播算法是基于梯度下降法的，它利用链式法则来计算目标函数相对于网络中每个权值的梯度。链式法则是微积分中用于计算复合函数导数的一个重要工具。

对于函数 \( y = f(g(x)) \)，链式法则告诉我们 \( \frac{dy}{dx} = \frac{df}{dg} \cdot \frac{dg}{dx} \)。在神经网络中，我们可以将每层的输出看作是下一层输入的函数，以此类推，直到最后一层的输出，这样就可以逐层应用链式法则来计算梯度。

### 2.2.2 反向传播算法的数学表达式

反向传播算法的核心步骤可以被数学地描述如下：

1. 前向传播：从输入层开始，每一层的神经元计算其输入和权值的加权和，然后通过激活函数得到该层的输出，并传递给下一层。
2. 计算误差：在输出层，计算输出误差，即目标函数 \( E(w) \) 对于输出 \( y_i \) 的导数 \( \frac{\partial E}{\partial y_i} \)。
3. 反向传播误差：误差梯度从输出层向输入层逐层反向传播，使用链式法则计算每一层的误差梯度 \( \frac{\partial E}{\partial w} \)。
4. 更新权值：使用计算出的梯度，按照梯度下降法更新神经网络中的所有权值。

### 2.2.3 误差反向传播过程详解

在反向传播算法中，每层误差的计算可以表达为：
\[ \delta_j^l = \frac{\partial E}{\partial z_j^l} \]
其中，\( \delta_j^l \) 表示第 \( l \) 层第 \( j \) 个神经元的误差项，\( z_j^l \) 表示该神经元的加权输入。

接下来，我们计算误差项的梯度，并传播给上一层。对于任何给定的权重 \( w_{jk}^{l+1} \)，梯度 \( \frac{\partial E}{\partial w_{jk}^{l+1}} \) 可以通过以下公式计算：
\[ \frac{\partial E}{\partial w_{jk}^{l+1}} = \delta_j^l \cdot y_k^{l} \]
这里 \( y_k^{l} \) 是第 \( l \) 层的第 \( k \) 个神经元的输出值。

通过这种方式，我们可以从输出层反向计算每一层的误差项，然后根据这些误差项来更新网络中的权值。

> **注意**：以上的数学推导仅提供了一个反向传播算法背后的理论框架。在实际实现算法时，需要仔细处理各种数值计算问题，并在必要时应用梯度裁剪、正则化等技术来提高性能和避免过拟合。

# 3. 反向传播算法的实践操作

## 3.1 反向传播算法的编程实现

### 3.1.1 编程语言和工具的选择

在实施反向传播算法时，选择合适的编程语言和工具至关重要。由于反向传播算法主要依赖于矩阵运算和微积分操作，因此需要具备高效数值计算能力的语言。Python因其简洁的语法和丰富的数据科学库而成为首选。此外，Python还提供了诸如NumPy和SciPy等库，这些库专门用于优化数组运算和科学计算。

在工具方面，TensorFlow和PyTorch是目前最为流行的深度学习框架。它们不仅提供了高级API用于快速实现复杂的神经网络结构，还支持自动求导功能，大大简化了反向传播算法的实现过程。这两者之间的主要区别在于设计理念，TensorFlow采用静态计算图，而PyTorch采用动态计算图，这影响了模型的灵活性和调试的便利性。

### 3.1.2 算法的代码结构和关键步骤

反向传播算法的代码通常包含以下几个关键部分：

1. **初始化网络结构和参数**：包括神经网络的层数、每层的节点数、激活函数等。
2. **前向传播**：输入数据在神经网络中逐层传播，每层的输出成为下一层的输入。
3. **计算损失函数**：通过比较网络输出和真实标签的差异来定义损失函数，常用的损失函数有均方误差(MSE)和交叉熵损失等。
4. **反向传播误差**：根据损失函数计算出的误差，通过链式法则计算每个权重的梯度。
5. **权值更新**：利用梯度下降法或其变种来更新网络中的权重和偏置。
6. **迭代优化**：重复前向传播和反向传播过程，直到损失函数达到满意的水平或迭代次数达到预设值。

下面是一个简单的反向传播算法的伪代码示例：

import numpy as np

# 激活函数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# 激活函数的导数
def sigmoid_derivative(x):
    return x * (1 - x)

# 定义网络参数
input_layer_size = 3
hidden_layer_size = 4
output_layer_size = 1

# 随机初始化权重和偏置
weights_input_hidden = np.random.rand(input_layer_size, hidden_layer_size)
weights_hidden_output = np.random.rand