挑战极限：提升反向传播算法效率的关键优化策略

# 1. 深度学习与反向传播算法基础

## 1.1 理解深度学习与反向传播
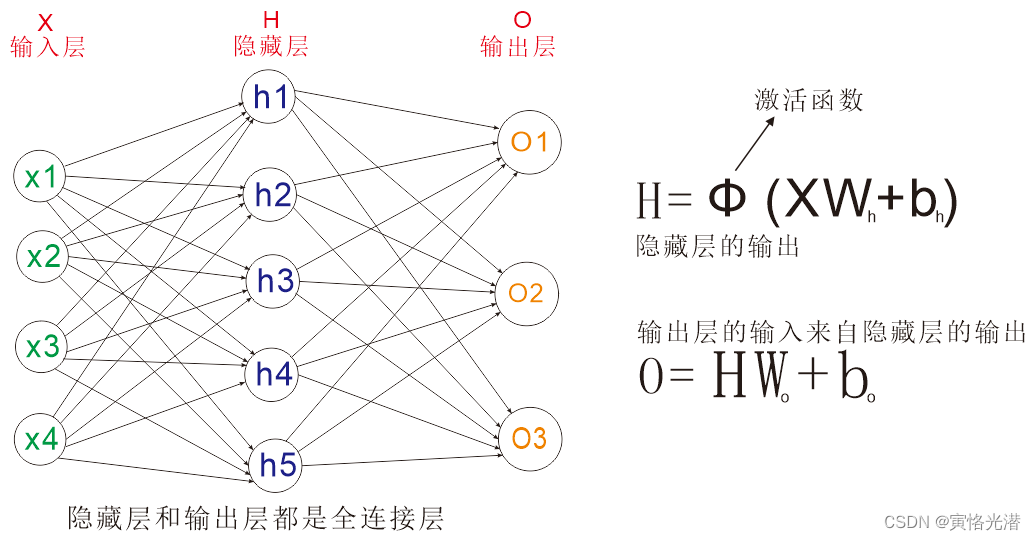
深度学习是机器学习的一个子领域，它通过构建多层的神经网络模型来学习数据的复杂特征。反向传播算法是训练这些神经网络的核心技术之一，它能够根据预测误差来调整网络中的权重和偏置。反向传播利用链式法则高效计算损失函数相对于权重的梯度，是实现梯度下降优化的基础。

## 1.2 反向传播的历史与发展
反向传播算法最早在1960年代被提出，但直到1986年被Rumelhart等人重新发现并推广后，它才真正成为了深度学习领域的基石。现代深度学习的快速发展离不开算法的不断优化和计算能力的提升。

## 1.3 反向传播在深度学习中的角色
在深度学习中，反向传播不仅用于训练神经网络，还提供了对网络性能影响的洞见。通过分析梯度的大小和方向，研究者可以对网络结构和参数进行诊断和调整，以获得更好的学习效果。

graph LR
    A[数据集] -->|输入| B[前向传播]
    B --> C[损失函数]
    C -->|误差反向传播| D[梯度计算]
    D --> E[权重更新]
    E --> F[网络性能提升]

以上流程图展示了反向传播算法在深度学习中如何通过梯度下降来调整网络权重，进而提升模型性能。接下来，我们将深入探讨反向传播算法的效率和优化方法。

# 2. 反向传播算法效率的理论分析

## 2.1 算法效率的重要性

### 2.1.1 时间复杂度与空间复杂度

在探讨深度学习模型的训练效率时，时间复杂度和空间复杂度是衡量算法效率的两个重要指标。时间复杂度关注的是执行一个算法所需的时间量，通常与模型参数数量和计算的复杂性有关。空间复杂度则关注在算法执行过程中所需的存储空间。

为了分析一个算法的效率，我们通常会使用大O符号来描述其时间复杂度和空间复杂度的上界。例如，对于一个简单的前馈神经网络，在没有优化的情况下，前向传播和反向传播的时间复杂度都是O(n)，其中n表示参数的数量。如果网络层次更深或网络宽度更大，这个复杂度会显著增加，从而影响训练过程的效率。

空间复杂度同样重要，尤其是在资源受限的环境下。深度学习模型常常需要大量的内存来存储参数、激活函数的输出、梯度值等。因此，空间优化也是提升深度学习算法效率的关键。

在理论分析阶段，研究者尝试通过算法优化来减少时间复杂度和空间复杂度，为实现高效训练提供可能。例如，通过减少模型参数数量、采用稀疏矩阵、使用低精度计算等方法，都可以在保证模型性能的同时，提升算法效率。

### 2.1.2 理论上的优化可能性

理论上，提升反向传播算法的效率可以通过以下几种方式实现：

1. **优化网络架构**：简化网络结构，减少不必要的层和参数数量，如采用深度可分离卷积替代标准卷积操作。
2. **减少计算量**：使用轻量级的激活函数，如ReLU的变种，减少非线性运算量。
3. **低精度数值表示**：利用低精度数据类型进行计算，如半精度（FP16）或整型（INT8）等，以加速运算并减少内存占用。
4. **数据并行与模型并行**：通过将数据或模型在多个处理器之间分割，以并行方式执行前向传播和反向传播。
5. **梯度计算优化**：使用有效梯度计算方法，例如延迟更新梯度，以减少计算次数。

在分析这些理论上的优化可能性时，研究人员需要考虑它们对模型准确性的影响，以及如何在保持准确率的前提下实现效率的提升。

## 2.2 反向传播算法的工作原理

### 2.2.1 前向传播过程

前向传播是深度学习中模型进行预测的关键步骤。在这个过程中，输入数据通过网络中的每一层，每层的神经元计算其加权输入和激活函数，并将结果传递到下一层。对于一个简单的全连接层，可以表示为：

import numpy as np

def forward_pass(input_data, weights, bias):
    # input_data: 输入层数据
    # weights: 权重矩阵
    # bias: 偏置项
    net_input = np.dot(weights, input_data) + bias
    output = activation_function(net_input)
    return output

其中`activation_function`表示激活函数，如ReLU、Sigmoid等。前向传播的效率直接影响整个训练过程的性能，因此对于大规模的神经网络来说，优化前向传播过程至关重要。

### 2.2.2 误差反向传播过程

在反向传播过程中，误差是沿着与前向传播相反的方向逐层传播的。在这个阶段，计算误差相对于每个权重的偏导数，也就是梯度。以下是简单的反向传播中梯度计算的例子：

def backward_pass(error, weights):
    # error: 当前层的误差项
    # weights: 本层的权重
    gradient = np.dot(error, weights.T)
    return gradient

反向传播算法的效率取决于如何快速且准确地计算出梯度。在大型网络中，这一过程涉及到大量的矩阵运算，优化这些运算可以显著提升效率。

### 2.2.3 参数更新与梯度下降

计算出梯度后，接下来是参数更新阶段，通常使用梯度下降或其变种（如Adam, RMSprop等）进行参数的迭代更新：

def update_parameters(weights, gradients, learning_rate):
    # weights: 权重矩阵
    # gradients: 计算出的梯度
    # learning_rate: 学习率
    new_weights = weights - learning_rate * gradients
    return new_weights

参数更新效率的提升，需要通过调整学习率、选择合适的优化器等方法来实现。同时，需要注意的是，参数更新过程需要在保证模型收敛性的前提下尽可能地高效。

## 2.3 神经网络训练中的效率瓶颈

### 2.3.1 数据加载与预处理

在深度学习模型的训练中，数据的加载与预处理阶段往往成为效率瓶颈。大量的数据加载需要花费大量的时间和系统资源。为了提高效率，可以采用以下策略：

1. 使用多线程或异步数据加载。
2. 对数据进行预处理并存储为二进制格式。
3. 使用数据增强来扩充训练集。

### 2.3.2 网络结构的复杂性

神经网络的复杂性也是影响训练效率的重要因素。网络结构的设计决定了模型的深度和宽度，进而影响参数的数量、模型的计算量等。设计合理的网络结构，能够在保持模型性能的同时，提升训练效率。

### 2.3.3 计算资源的限制

最后，计算资源的限制对算法效率也有直接影响。例如，在GPU资源受限的情况下，可能需要调整批量大小（batch size）来适应计算能力，或者使用分布式训练来充分利用多GPU资源。

graph TD;
A[开始训练] --> B[数据加载与预处理]
B --> C[前向传播]
C --> D[损失计算]
D --> E[误差反向传播]
E --> F[参数更新]
F --> G{是否收敛}
G -- 是 --> H[模型训练完成]
G -- 否 --> B

以上流程图展示了一个典型的深度学习模型训练过程，其中每个步骤都可能成为效率的瓶颈。通过理论分析和实践操作，我们不断寻找提升算法效率的新方法和优化策略。

# 3. 提升