从理论到应用：深度学习反向传播算法的演变史

# 1. 深度学习与反向传播算法概述

深度学习是机器学习中的一种重要方法，其核心思想是模拟人脑的神经网络结构，通过学习大量的数据来提取特征，进而实现对数据的理解和预测。反向传播算法是深度学习中的一种重要算法，它通过误差反向传播，使网络中的每个神经元的权重和偏置不断更新，从而达到学习的目的。

反向传播算法的原理并不复杂，它是基于梯度下降法的一种优化算法。首先，我们将数据输入到神经网络中，通过前向传播得到输出结果。然后，我们将输出结果与真实值进行比较，计算出误差。接着，误差通过反向传播的方式，从输出层传到输入层，每个神经元的权重和偏置根据误差进行调整。这个过程不断重复，直到网络的输出误差达到一个可接受的范围。

反向传播算法的成功，极大地推动了深度学习的发展。然而，反向传播算法也存在一些问题，如梯度消失和梯度爆炸等问题。这些问题的解决，需要我们对算法进行深入的理解和研究。

# 2. 反向传播算法的数学原理

反向传播算法是深度学习中最为关键的技术之一，其核心在于高效的计算神经网络中的权重梯度。为了深入理解这一算法，需要先从神经网络的基础知识开始，逐步深入到算法的推导，再到优化算法和正则化技术的探讨。

## 2.1 神经网络基础知识

### 2.1.1 激活函数的作用与选择

在神经网络中，激活函数负责引入非线性因素，使网络可以学习和执行复杂的任务。常见的激活函数包括Sigmoid、Tanh、ReLU及其变种，以及最近被提出的Swish等。

- **Sigmoid函数**：将任何实数值压缩至(0,1)之间，适合用作二分类问题的输出层。
- **Tanh函数**：输出范围在(-1,1)，比Sigmoid有更明显的中心对称性。
- **ReLU函数**：当输入大于0时，输出等于输入；否则输出为0。它计算简单且有助于缓解梯度消失问题。
- **Swish函数**：由Google提出，表现介于ReLU和Sigmoid之间。

选择激活函数时需要考虑以下因素：
- 非线性：激活函数必须是非线性的，否则神经网络的表达能力就得不到保证。
- 导数：必须容易计算，以确保梯度下降法的有效性。
- 梯度消失和梯度爆炸：避免梯度在深层网络中过小或过大。
- 计算效率：对于大型网络，计算效率是一个重要的考量因素。

### 2.1.2 损失函数的理解与应用

损失函数衡量的是神经网络的预测输出与实际目标值之间的差异。它在训练过程中被用来更新权重。常用的损失函数包括均方误差(MSE)、交叉熵损失等。

- **均方误差(MSE)**：常用于回归任务，它计算的是预测值与真实值差值的平方的平均数。
- **交叉熵损失**：用于分类问题，尤其是概率输出的分类器，它衡量的是概率分布之间的差异。

损失函数的选择应基于实际问题的需求。比如，分类问题中，一般会选择交叉熵损失；回归问题中，则通常采用MSE。

## 2.2 反向传播算法的推导

### 2.2.1 梯度下降法及其变种

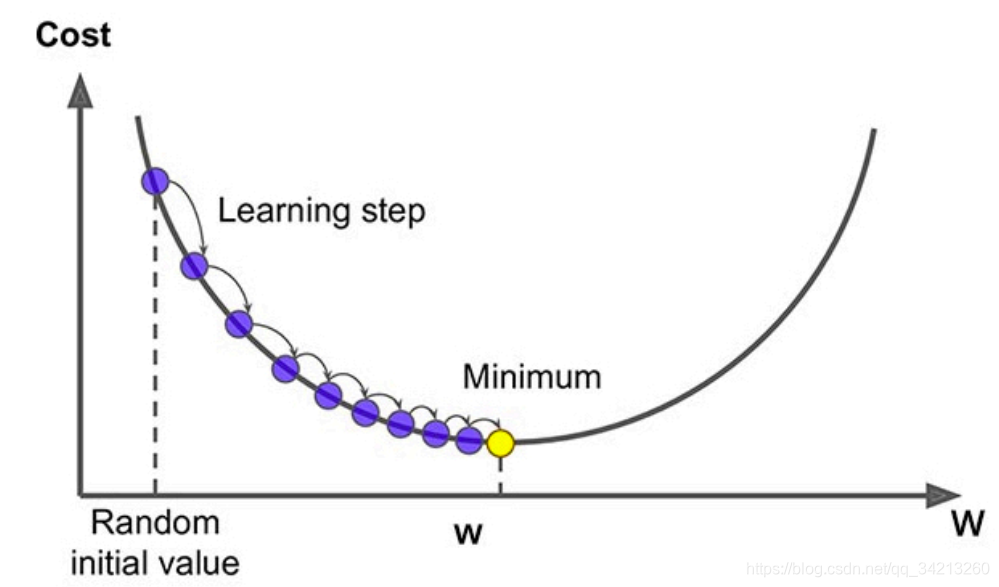
梯度下降法是最基本的优化算法，通过计算损失函数关于参数的梯度，并在此梯度的反方向上更新参数，来最小化损失函数。

基本梯度下降的更新公式是：θ = θ - η * ∂L/∂θ，其中θ表示参数，η表示学习率，L表示损失函数，∂L/∂θ表示损失函数关于参数的导数。

梯度下降法的变种包括随机梯度下降法(SGD)和小批量梯度下降法(mini-batch GD)，它们通过使用一部分数据或者单个样本数据来计算梯度，提高了计算效率。

### 2.2.2 链式法则在反向传播中的应用

反向传播算法实际上是一个链式法则的递归应用。在神经网络中，链式法则是用于高效计算损失函数对每个参数偏导数的方法。

链式法则简单来说是：如果一个变量y是由几个函数的复合构成，那么y关于其中一个变量的导数，等于y对这个函数的导数乘以这个函数对那个变量的导数。这个原理允许我们在神经网络的每一层计算误差对权重的梯度，从而有效地进行梯度下降。

## 2.3 优化算法与正则化技术

### 2.3.1 动量、RMSprop与Adam优化算法

**动量**：加速梯度下降，它通过累积历史梯度信息来加速学习，并减少震荡，因为惯性的作用，它可以越过小的坑洼。

**RMSprop**：是为了解决Adagrad学习率单调递减的问题而提出的，它调整学习率，使其自适应地变化。

**Adam**：结合了Momentum和RMSprop的优点，它通过计算梯度的一阶矩估计和二阶矩估计来实现自适应的学习率。

### 2.3.2 L1、L2正则化及其对模型的影响

**L1正则化**：倾向于产生稀疏的权重矩阵，即很多参数会变成零。它可以帮助我们进行特征选择。

**L2正则化**：防止模型复杂度过高，有助于减少模型对训练数据的拟合程度，提高模型的泛化能力。

正则化技术通过给损失函数增加一个惩罚项来避免过拟合，即在模型的复杂度和对训练数据的拟合度之间寻找一个平衡点。

在深入探讨了反向传播算法的数学原理后，我们接下来将进入实践操作部分，了解如何编程实现反向传播算法，并对算法进行调优和诊断。

# 3. 反向传播算法的实践操作

## 3.1 反向传播算法的编程实现

### 3.1.1 利用框架搭建基本的神经网络

在深度学习中，使用现代机器学习框架（如TensorFlow、PyTorch等）可以简化神经网络的搭建过程。尽管如此，理解底层的工作原理对优化模型和调试问题依旧至关重要。下面以PyTorch为例，介绍如何使用框架搭建一个简单的多层感知器（MLP）。

import torch
import torch.nn as nn
import torch.optim as optim

# 定义一个简单的多层感知器网络结构
class SimpleMLP(nn.Module):
    def __init__(self, input_size, hidden_size, num_classes):
        super(SimpleMLP, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size) 
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(hidden_size, num_classes)  
    def forward(self, x):
        out = self.fc1(x)
        out = self.relu(out)
        out = self.fc2(out)
        return out

# 实例化网络
input_size = 784  # 以MNIST数据集为例，图片大小为28x28
hidden_size = 500
num_classes = 10
net = SimpleMLP(input_size, hidden_size, num_classes)

这段代码定义了一个包含一个隐藏层的神经网络。在`__init__`方法中，我们初始化了两个全连接层和一个ReLU激活函数。`forward`方法定义了数据通过网络的路径。

### 3.1.2 实现自定义的反向传播过程

虽然大多数深度学习框架提供了自动梯度计算和反向传播算法的实现，但在某些情况下，我们可能需要手动实现反向传播过程。以下是如何手动实现上述网络的反向传播：

criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)

def custom_backward(input_data, target):
    # 正向传播
    output = net(input_data)
    loss = criterion(output, target)
    # 反向传播
    optimizer.zero_grad()  # 清除过往梯度信息
    loss.backward()        # 反向传播计算梯度
    # 更新权重
    optimizer.step()
    return loss.item()

# 假设input_data和target已经被加载和预处理
loss = custom_backward(input_data, target)

在这个例子中，我们首先定义了损失函数和优化器。`custom_backward`函数实现了单步的训练过程，包括正向传播、损失计算、梯度清除、反向传播和权重更新。

## 3.2 反向传播算法的调优与诊断

### 3.