多层感知机的精准调整：反向传播算法的应用与优化技巧

# 1. 多层感知机和反向传播算法基础

在这一章节中，我们将探索多层感知机（MLP）的基本概念以及其背后的反向传播算法。我们将开始于感知机的基础，它是构成MLP的基本单元，并逐渐展开讨论激活函数如何使网络学习复杂的模式和特征。最后，我们将介绍损失函数对于引导网络学习的至关重要性。

## 多层感知机简介

多层感知机（MLP）是人工神经网络的一种基本形式，它由至少一个或多个的隐藏层组成。每个隐藏层包含了若干个感知机，每个感知机都是简单的神经元模型，通常由权重、偏置和一个非线性激活函数组成。MLP对于复杂数据集具有强大的学习能力，主要归功于它们能够通过隐藏层对数据进行多层抽象和变换。

## 感知机的工作原理

感知机根据输入和权重进行加权求和，然后通过一个激活函数来计算输出。这个过程可以表示为：

def perceptron(input, weights, bias):
    # 输入向量、权重向量和偏置
    weighted_sum = sum(input * weights) + bias
    # 激活函数（例如sigmoid）
    output = sigmoid(weighted_sum)
    return output

# 示例激活函数sigmoid
def sigmoid(x):
    return 1 / (1 + exp(-x))

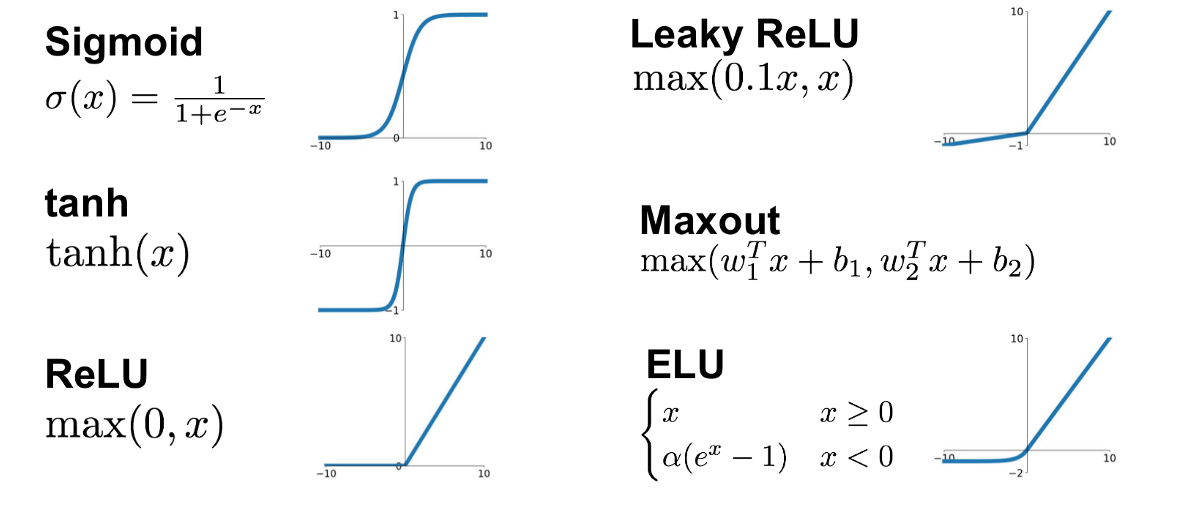
激活函数是感知机层实现非线性变换的关键。常见的激活函数包括sigmoid、ReLU、tanh等。

## 激活函数的角色和选择

激活函数的选择直接影响着神经网络的学习效率和模型性能。它们负责将线性输出转换为非线性输出，从而使网络能够学习和模拟复杂的数据关系。ReLU（Rectified Linear Unit）由于其计算简单和梯度不消失等优点，目前在实践中被广泛采用。Sigmoid和tanh由于梯度消失问题，在深层网络中使用较少。

在了解了感知机和激活函数之后，我们将进一步探索损失函数在多层感知机中的作用，它是如何影响整个网络学习和优化过程的重要因素。

# 2. 反向传播算法的理论与实践

## 2.1 反向传播算法的理论框架

### 2.1.1 感知机的工作原理
感知机是人工神经网络中最基础的单元，它模仿了生物神经元的工作方式。单个感知机接收若干输入信号，每个信号都有一个权重与之关联。在接收信号后，感知机将加权输入进行累加，并通过一个激活函数产生输出。如果输入信号的加权和超过某个阈值，感知机激活并输出1，否则输出0。

在数学上，感知机的行为可以通过以下公式描述：

$$ f(x) = \left\{
\begin{array}{ll}
1 & \text{if } \sum_{i=1}^{n} w_{i}x_{i} > \theta \\
0 & \text{otherwise}
\end{array}
\right. $$

其中，\(x_{i}\) 是输入信号，\(w_{i}\) 是权重，\(\theta\) 是阈值。

### 2.1.2 激活函数的角色和选择
激活函数在神经网络中扮演着极其重要的角色，它为感知机引入非线性因素，使网络能够学习和模拟复杂的函数。常见的激活函数包括Sigmoid、ReLU及其变体、tanh等。

- **Sigmoid函数**：输出范围为(0,1)，适用于输出层，如果需要概率解释时。
- **ReLU函数**：当输入为正时，输出等于输入，否则输出为0。它的计算效率高于Sigmoid，而且在实践中发现对梯度消失问题有更好的缓解效果。

选择合适的激活函数依赖于具体的应用和实验结果。激活函数的选择直接影响了模型的学习速度和效率。

### 2.1.3 损失函数的种类及其重要性
损失函数，也称为代价函数，用于衡量模型预测值与真实值之间的差异。损失函数的选择对反向传播算法的性能至关重要，因为它提供了学习的方向。

- **均方误差（MSE）**：常用于回归问题，对预测误差的平方求平均。
- **交叉熵**：常用于分类问题，因为它可以提供更好的梯度信息。

损失函数的选择需要和问题类型相匹配，同时考虑梯度下降的稳定性和速度。

## 2.2 反向传播算法的数学基础

### 2.2.1 基于梯度的优化
梯度是损失函数相对于参数的导数，它指出了损失函数下降最快的方向。基于梯度的优化方法，如梯度下降法，通过迭代更新参数来最小化损失函数。

梯度下降的参数更新公式为：

$$ \theta = \theta - \eta \cdot \nabla J(\theta) $$

其中，\(\theta\) 是参数，\(\eta\) 是学习率，\(\nabla J(\theta)\) 是损失函数关于参数的梯度。

### 2.2.2 链式法则和误差反向传播
链式法则是微积分中计算复合函数导数的法则。在神经网络中，利用链式法则可以计算损失函数关于任一权重的偏导数。误差反向传播是链式法则在反向传播算法中的应用，它能够高效计算梯度。

以三层网络为例，误差反向传播的计算过程可以概括为：

1. 计算输出层的误差。
2. 反向传播误差到隐藏层。
3. 更新所有层的权重。

### 2.2.3 权重更新规则的推导
权重更新规则是基于梯度下降的改进算法，如随机梯度下降（SGD）、动量法等。这些方法试图解决传统梯度下降在复杂优化问题中容易陷入局部最小值或收敛速度慢的问题。

权重更新规则的推导可以从对损失函数进行泰勒展开开始，进而得到在当前参数下，损失函数近似最优下降方向的表达式。然后，根据下降方向和学习率，更新参数。

## 2.3 实现反向传播算法的步骤

### 2.3.1 初始化网络参数
初始化网络参数是训练神经网络的第一步。权重的初始化方法有很多，包括全零初始化、随机初始化、Xavier初始化和He初始化等。不同的初始化方法会影响模型的训练速度和收敛性。

Xavier初始化考虑了前一层的激活单元数，He初始化则是Xavier的改进版，主要针对ReLU激活函数。

### 2.3.2 前向传播和损失计算
前向传播是指从输入层开始，逐层计算直至输出层的过程。这一过程中，每一层的输出都作为下一层的输入。在输出层，根据实际输出和期望输出计算损失函数的值。

### 2.3.3 反向传播和参数更新
反向传播算法基于梯度下降法和链式法则，将损失函数的梯度传播回网络中，更新每层的权重和偏置。这一过程是迭代进行的，直至网络在训练集上的损失达到满意的水平或达到预定的迭代次数。

反向传播步骤如下：

1. 从输出层开始，计算损失函数关于每个参数的偏导数。
2. 利用链式法则计算每一层的误差。
3. 根据计算得到的梯度，更新网络参数。
4. 重复上述步骤，直至网络收敛。

# 3. 反向传播算法的参数调整和优化技巧

## 3.1 学习率的选择和调整策略

### 3.1.1 学习率对训练过程的影响

学习率是神经网络训练中最为关键的超参数之一。它决定了在参数空间中每一步的步长大小，影响着优化算法是否能够找到一个较好的最小值，以及训练过程的收敛速度。一个太高的学习率可能导致模型无法收敛，甚至在最优值附近振荡；而一个太低的学习率会使得训练非常缓慢，甚至陷入局部最优。通常需要通过实验来调整学习率，或者使用一些自适应学习率的算法。

### 3.1.2 动量法和自适应学习率算法

动量法是一种通过积累之前梯度的动量来加速学习的方法。它引入了一个动量项，用来缓存之前梯度的方向，并且在新的方向上产生一个加速度，这有助于越过鞍点。动量法的一个重要超参数是动量值，它决定了历史梯度信息对当前更新影响的程度。

自适应学习率算法，如Adam、RMSprop等，能够根据梯度的历史信息自动调整学习率。这些算法的核心思想是保持学习率在训练过程中相对稳定，同时允许在梯度稀疏的方向上增加学习率，而在梯度大的方向上减少学习率，从而有效地提升模型的收敛速度，并避免在训练过程中过度振荡。

### 3.1.3 学习率衰减与周期调整

学习率衰减是一种在训练过程中逐渐减小学习率的策略，有助于模型在达到或接近最优解时微调参数。常用的衰减策略包括固定衰减、时间衰减和性能衰减等。周期调整则是指周期性地改变学习率的大小，例如在每个epoch后或达到一定的迭代次数后对学习率进行调整。

### 代码块展示学习率调整策略

# 学习率调整策略：学习率衰减函数的示例（PyTorch）
def adjust_learning_rate(optimizer, epoch, initial_lr):
    """Sets the learning rate to the initial LR decayed by 10 every 30 epochs"""
    lr = initial_lr * (0.1 ** (epoch // 30))
    for param_group in optimizer.param_groups:
        param_group['lr'] = lr

# 假设优化器和初始学习率已经定义
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
initial_lr = optimizer.param_groups[0]['lr']

# 在训练循环中调整学习率
for epoch in range(num_epochs):
    adjust_learning_rate(optimizer, epoch, initial_lr)
    # ... 其余训练代码 ...

此代码块中的学习率衰减函数根据训练的epoch数进行调整。学习率每30个epoch衰减10倍。这种策略有助于网络在训练初期快速收敛，在后期进行精细调整，以减少过拟合和提升模型性能。

## 3.2 正则化技术及其应用

### 3.2.1 L1与L2正则化原理

在训练神经网络时，正则化技术被用于防止过拟合。L1正则化倾向于生成稀疏权重矩阵，即倾向于产生许多零权重，这可以用来进行特征选择。L2正则化（也称为权重衰减）倾向于限制权重的大小，使得模型的权重更加平滑。在实践中，L2正则化通常比L1更受欢迎，因为它更容易与基于梯度下降的优化算法结合。

### 3.2.2 丢弃法（Dropout）和数据增强

丢弃法（Dropout）是一种在训练过程中临时随机丢弃网络中的一部分神经元的方法，有助于防止网络对训练样本产生依赖，从而提升模型的泛化能力。数据增强是通过生成新的训练样本（如旋转、缩放图片）来增加模型的训练数据量，从而提升模型的泛化能力。

### 3.2.3 批标准化（Batch Normalization）

批标准化（Batch Normalization）是一种在深度学习模型训练时对层输入进行规范化处理的技术。它通过对每个小批量数据执行标准化处理，以减少内部协变量偏移，提高模型的训练速度，同时有时也能改善模型的泛化能力。通过标准化输入，可以使网络中的权重参数保持在一个合理的数值范围内，避免梯度消失或爆炸的问题。

### 代码块展示Batch Normalization用法

# Batch Normalization的使用示例（PyTorch）
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 20, 5, 1)
        self.bn1 = nn.BatchNorm2d(20)
        self.fc1 = nn.Linear(4*4*20, 500)
        self.bn2 = nn.BatchNorm1d(500)
        self.fc2 = nn.Linear(500, 10)

    def forward(self, x):
        x = F.relu(F.max_pool2d(self.bn1(self.conv1(x)),