密码分析中的随机数生成：破解加密算法

# 1. 密码分析基础

密码分析是研究密码系统安全性的学科，旨在找出密码系统的弱点并破解加密算法。随机数生成在密码分析中扮演着至关重要的角色，因为许多密码算法都依赖于随机数来保证安全性。本章将介绍密码分析的基础知识，为后续章节中深入探讨随机数生成在密码算法中的应用和攻击奠定基础。

# 2. 随机数生成理论**

### 2.1 伪随机数生成器 (PRNG)**

伪随机数生成器 (PRNG) 是算法，可生成看似随机的数字序列，但实际上是由确定性算法生成的。PRNG 广泛用于密码学、模拟和游戏等应用中。

**2.1.1 线性同余生成器 (LCG)**

LCG 是最简单的 PRNG 之一，它使用以下公式生成随机数：

X[n] = (a * X[n-1] + c) % m

其中：

* `X[n]` 是第 `n` 个随机数
* `X[n-1]` 是第 `n-1` 个随机数
* `a` 是乘数
* `c` 是增量
* `m` 是模数

**代码示例：**

import random

# 定义 LCG 参数
a = 1103515245
c = 12345
m = 2**32

# 初始化种子
seed = 12345

# 生成 10 个随机数
for i in range(10):
    seed = (a * seed + c) % m
    print(seed)

**逻辑分析：**

* `random.seed(seed)` 设置随机数生成器的种子，以确保每次运行时生成相同的随机数序列。
* `(a * seed + c) % m` 根据 LCG 公式生成随机数。
* `print(seed)` 打印生成的随机数。

### 2.1.2 梅森旋转生成器 (MT)**

MT 是另一种流行的 PRNG，它使用称为梅森旋转算法的复杂算法生成随机数。MT 以其出色的统计特性和较长的周期而闻名。

**代码示例：**

import numpy as np

# 初始化 MT 生成器
mt = np.random.MT19937(seed=12345)

# 生成 10 个随机数
for i in range(10):
    print(mt.randint(0, 100))

**逻辑分析：**

* `np.random.MT19937(seed=12345)` 使用指定的种子初始化 MT 生成器。
* `mt.randint(0, 100)` 生成介于 0 和 100 之间的随机整数。

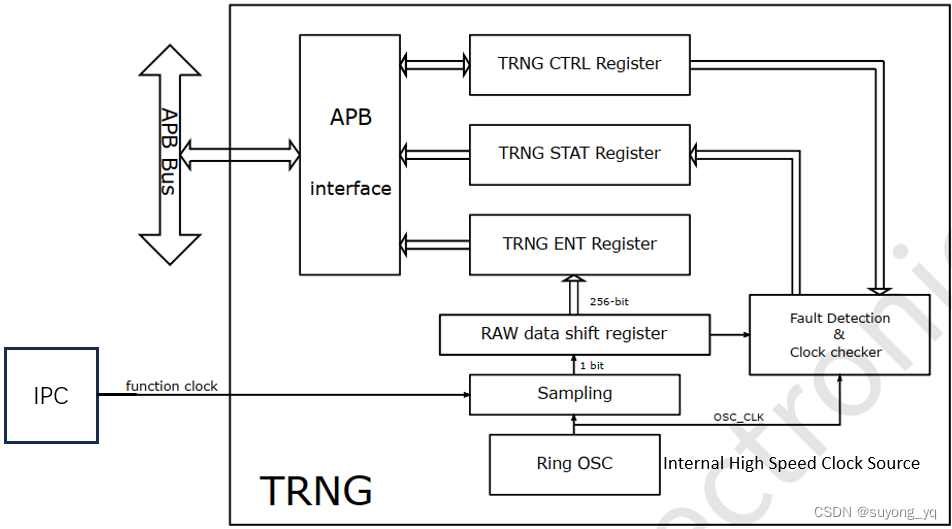
### 2.2 真随机数生成器 (TRNG)**

真随机数生成器 (TRNG) 是生成真正随机数的设备或算法。TRNG 利用物理噪声源或量子力学原理来生成随机性。

**2.2.1 物理噪声源**

物理噪声源，如热噪声、雪崩噪声和闪烁噪声，可用于生成随机数。这些噪声源产生不可预测的信号，可转换为数字随机数。

**2.2.2 量子随机数生成器**

量子随机数生成器 (QRNG) 利用量子力学原理生成随机数。例如，基于贝尔不等式的 QRNG 通过测量纠缠光子的自旋来生成随机位。

# 3. 密码算法中的随机数生成**

### 3.1 对称加密算法中的随机数

对称加密算法使用相同的密钥进行加密和解密，因此随机数在对称加密中起着至关重要的作用。

#### 3.1.1 初始化向量 (IV)**

初始化向量 (IV) 是一个随机值，用于初始化块加密算法的内部状态。IV 确保每次加密操作都产生不同的密文，即使使用相同的密钥和明文。

#### 3.1.2 填充算法

填充算法用于在加密前将明文填充到块大小的整数倍。填充算法使用的随机数据确保密文不会泄露明文的长度或结构。

### 3.2 非对称加密算法中的随机数

非对称加密算法使用不同的密钥进行加密和解密，因此随机数在非对称加密中也至关重要。

#### 3.2.1 密钥生成

在非对称加密中，密钥对 (公钥和私钥) 是随机生成的。随机数生成器必须确保密钥对是唯一的、不可预测的。

#### 3.2.2 数字签名

数字签名使用私钥对消息进行加密，而公钥用于验证签名。随机数用于生成签名，确保签名是唯一的、不可伪造的。

### 代码示例：

**使用 OpenSSL 生成 IV**

# 生成 16 字节的 IV
openssl rand -hex 16
`