揭秘随机数生成器的秘密：生成随机数的艺术

# 1. 随机数生成的基础**

**1.1 随机数的概念和类型**

随机数是指具有不可预测性且分布均匀的数字序列。它们可分为两类：

* **真随机数：**由物理现象或生物特征产生的真正不可预测的数字。
* **伪随机数：**由算法生成的看似随机但实际上是可预测的数字。

**1.2 随机数生成器的原理**

随机数生成器是产生随机数的算法或设备。它们利用数学函数或物理过程来创建不可预测的数字序列。常见原理包括：

* **线性同余法：**使用线性方程产生伪随机数。
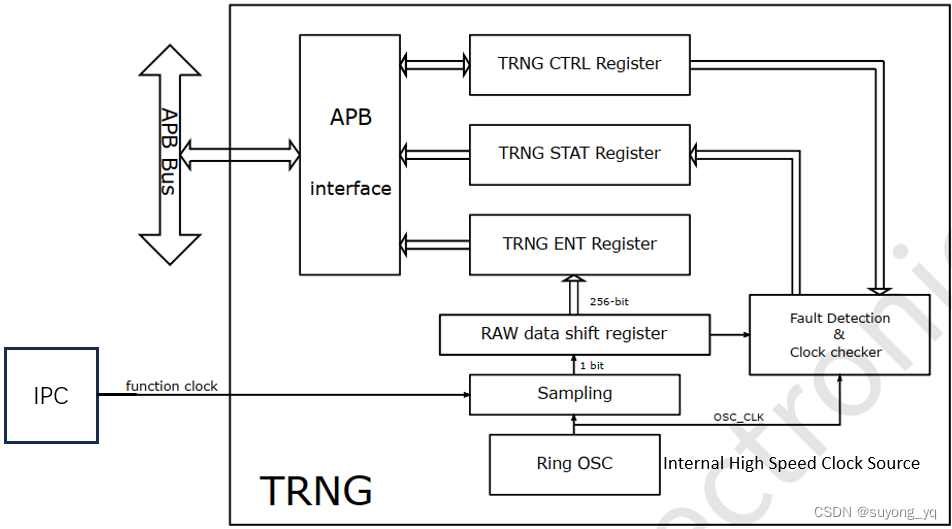
* **物理现象采集：**利用自然现象（如噪声或热量）产生真随机数。

# 2. 伪随机数生成算法

伪随机数生成算法（PRNG）是计算机中生成随机数最常用的方法。这些算法使用确定性的数学公式来生成看似随机的数字序列，但实际上是可预测的。

### 线性同余法

线性同余法是一种简单的 PRNG，使用以下公式生成随机数：

X[n+1] = (a * X[n] + c) mod m

其中：

* X[n] 是第 n 个随机数
* a、c 和 m 是常数

线性同余法的优点是速度快，但缺点是可预测性较差。

### 梅森旋转算法

梅森旋转算法是一种更复杂的 PRNG，使用以下公式生成随机数：

X[n+1] = (X[n] ^ (X[n] >> u)) & (X[n] >> s) ^ (X[n] >> t)

其中：

* X[n] 是第 n 个随机数
* u、s 和 t 是常数

梅森旋转算法比线性同余法更难预测，但速度也较慢。

### 泊松分布算法

泊松分布算法是一种基于泊松分布的 PRNG。它使用以下公式生成随机数：

X[n+1] = Poisson(λ)

其中：

* X[n+1] 是第 n+1 个随机数
* λ 是泊松分布的参数

泊松分布算法生成的是离散随机数，其优点是随机性较好，但缺点是速度较慢。

### 蒙特卡罗方法

蒙特卡罗方法是一种基于随机采样的 PRNG。它使用以下步骤生成随机数：

1. 在一个定义域内生成一个随机点
2. 计算该点在目标函数上的值
3. 重复步骤 1 和 2，直到获得足够数量的点
4. 根据这些点的分布来估计目标函数的值

蒙特卡罗方法的优点是随机性较好，但缺点是速度较慢，并且需要大量的计算资源。

# 3. 真随机数生成技术

真随机数生成技术旨在生成不可预测且不受算法或外部因素影响的随机数。与伪随机数不同，真随机数的生成过程依赖于物理现象或其他不可预测的事件。

**物理现象采集**

物理现象采集是生成真随机数的一种常见方法。它利用诸如噪声、热量和放射性等物理现象的固有随机性。

* **噪声源：**噪声源，如二极管或电阻器，会产生不可预测的电压波动。这些波动可以数字化并用作随机数。
* **热噪声：**热噪声是由于电子在导体中随机运动而产生的。通过测量热噪声的幅度，可以生成真随机数。
* **放射性衰变：**放射性元素的衰变是另一个不可预测的物理现象。通过检测放射性衰变事件的时间间隔，可以生成真随机数。

**生物特征识别**

生物特征识别技术利用个人独特的生物特征，如指纹或虹膜，来生成真随机数。

* **指纹：**指纹的细微差异可以数字化并用作随机数。每个人的指纹都是独一无二的，因此生成的随机数也是不可预测的。
* **虹膜：**虹膜的复杂图案也可以数字化并用作随机数。虹膜图案同样是独一无二的，从而保证了生成的随机数的不可预测性。

**量子随机数生成**

量子随机数生成 (QRNG) 利用量子力学的固有随机性来生成真随机数。

* **量子叠加：**量子比特可以处于多个状态的叠加态。通过测量量子比特的状态，可以生成真随机数。
* **量子纠缠：**量子纠缠是两个或多个量子比特之间的一种相关性。通过测量一个量子比特的状态，可以立即确定另一个量子比特的状态，从而生成真随机数。

**代码示例：**

import random

# 使用物理现象采集生成真随机数
noise_source = random.SystemRandom()
random_number = noise_source.random()

# 使用生物特征识别生成真随机数
fingerprint_reader = random.SystemRandom()
random_number = fingerprint_reader.random()

# 使用量子随机数生成生成真随机数
qrng = random.SystemRandom()
random_number = qrng.random()

**逻辑分析：**

* `random.SystemRandom()` 函数用于生成真随机数。
* `random()` 方法生成一个介于 0 和 1 之间的浮点数随机数。

**参数说明：**

* `random.SystemRandom()` 函数没有参数。
* `random()` 方法没有参数。

**拓展讨论：**

真随机数生成技术比伪随机数生成算法更安全且不可预测。它们广泛用于需要高安全性或不可预测性的应用中，例如：

* 加密和信息安全
* 赌博和彩票
* 科学研究和数据分析
* 军事和国防

# 4. 随机数生成器的应用

随机数生成器在各个领域都有着广泛的应用，为这些领域提供了不可或缺的随机性来源。

### 加密和信息安全

随机数是加密算法的基础，用于生成加密密钥、初始化向量和一次性密码本。在密码学中，随机性至关重要，因为它可以防止攻击者预测或猜测密钥，从而确保数据的机密性、完整性和不可否认性。

#### 代码示例

import random

# 生成一个 256 位的加密密钥
key = random.getrandbits(256)

# 生成一个 128 位的初始化向量
iv = random.getrandbits(128)

# 生成一个 1024 位的一次性密码本
one_time_pad = random.getrandbits(1024)

### 模拟和建模

随机数生成器在模拟和建模中扮演着至关重要的角色，用于生成随机变量和模拟复杂系统。在科学研究、工程和金融等领域，随机性是不可或缺的，因为它可以帮助研究人员探索不同场景、预测结果并做出明智的决策。

#### 代码示例

import numpy as np

# 生成 100 个服从正态分布的随机数
random_numbers = np.random.normal(0, 1, 100)

# 使用这些随机数模拟一个布朗运动过程
brownian_motion = np.cumsum(random_numbers)

### 游戏和娱乐

随机数生成器在游戏和娱乐行业中也发挥着重要作用，用于生成随机事件、创建逼真的环境和提供令人兴奋的体验。从掷骰子到生成游戏角色的属性，随机性是游戏设计中不可或缺的一部分。

#### 代码示例

import random

# 掷一个六面骰子
roll = random.randint(1, 6)

# 生成一个 0 到 100 之间的随机数
random_number = random.uniform(0, 100)

# 生成一个随机颜色
random_color = random.choice(["red", "green", "blue"])

### 科学研究和数据分析

在科学研究和数据分析中，随机数生成器用于生成随机样本、进行统计检验和创建机器学习模型。随机性有助于确保研究结果的可靠性和有效性，并为数据分析提供宝贵的见解。

#### 代码示例

import random

# 从一个包含 100 个元素的列表中随机抽取 10 个元素
random_sample = random.sample(list(range(100)), 10)

# 使用随机数生成器进行蒙特卡罗积分
def monte_carlo_integral(f, a, b, n):
    total = 0
    for _ in range(n):
        x = random.uniform(a, b)
        total += f(x)
    return total * (b - a) / n

# 5. 随机数生成器的评价与优化

### 5.1 随机性测试

随机数生成器的核心在于其随机性。为了评估随机数的质量，需要进行严格的测试来验证其是否符合统计学上的随机性。常用的测试方法包括：

- **频率分布测试：**检查随机数的频率分布是否符合预期的均匀分布。
- **序列测试：**分析随机数序列中是否存在明显的模式或相关性。
- **随机性检验：**使用统计检验（如卡方检验或科尔莫戈罗夫-斯米尔诺夫检验）来验证随机数的随机性。

### 5.2 效率和速度

随机数生成器在实际应用中通常需要处理大量数据。因此，其效率和速度至关重要。以下因素会影响随机数生成器的性能：

- **算法选择：**不同的随机数生成算法具有不同的时间复杂度。
- **实现方式：**优化算法的实现可以提高效率。
- **硬件支持：**使用硬件加速器（如随机数生成器芯片）可以大幅提升速度。

### 5.3 安全性和可靠性

在加密和信息安全等应用中，随机数生成器的安全性至关重要。以下因素会影响随机数生成器的安全性：

- **不可预测性：**随机数序列不应该被预测或重现。
- **熵来源：**随机数生成器应从可靠的熵源（如物理现象或生物特征）中获取熵。
- **抗攻击性：**随机数生成器应能够抵抗各种攻击，如侧信道攻击或后门攻击。

### 5.4 优化策略

通过以下策略可以优化随机数生成器的性能：

- **选择合适的算法：**根据应用需求选择时间复杂度和安全性合适的算法。
- **并行化：**使用多线程或多进程来并行生成随机数。
- **硬件加速：**利用硬件加速器来提高生成速度。
- **缓存：**将生成好的随机数缓存起来，以减少重复生成。