BP神经网络在MATLAB中的部署：将训练好的网络应用于实际问题的完整指南

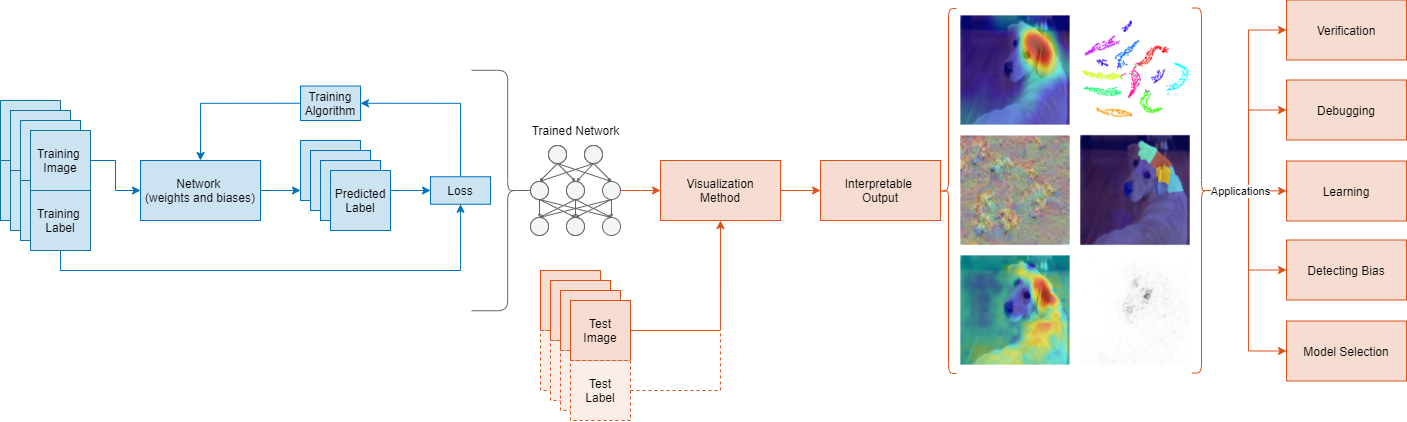
# 1. BP神经网络概述

BP神经网络（反向传播神经网络）是一种多层前馈神经网络，广泛应用于模式识别、预测建模和优化问题中。其基本原理是通过输入层、隐含层和输出层之间的权重和偏置不断调整，使网络的输出与期望输出之间的误差最小化。

BP神经网络的学习过程分为前向传播和反向传播两个阶段。在**前向传播**中，输入信号从输入层逐层向前传递，经过隐含层计算后到达输出层。在**反向传播**中，输出层的误差信号通过隐含层逐层反向传播，并根据误差信号调整权重和偏置，使得误差逐渐减小。

# 2. MATLAB中BP神经网络的实现

### 2.1 BP神经网络的数学原理

BP神经网络是一种多层前馈神经网络，其数学原理基于误差反向传播算法。它由输入层、隐含层和输出层组成，其中隐含层可以有多层。

**前向传播：**

1. 将输入数据传递到输入层。
2. 计算隐含层节点的激活值：`a_j^{(l)} = f(w_j^{(l)} \cdot a^{(l-1)} + b_j^{(l)})`
- `a^{(l-1)}`：上一层节点的激活值
- `w_j^{(l)}`：从上一层到当前节点的权重
- `b_j^{(l)}`：当前节点的偏置
- `f`：激活函数（如sigmoid、ReLU）

3. 计算输出层节点的激活值：`a_k^{(L)} = f(w_k^{(L)} \cdot a^{(L-1)} + b_k^{(L)})`
- `a^{(L-1)}`：隐含层节点的激活值
- `w_k^{(L)}`：从隐含层到输出层节点的权重
- `b_k^{(L)}`：输出层节点的偏置

**反向传播：**

1. 计算输出层的误差：`δ_k^{(L)} = (y_k - a_k^{(L)}) \cdot f'(a_k^{(L)})`
- `y_k`：期望输出
- `f'`：激活函数的导数

2. 计算隐含层的误差：`δ_j^{(l)} = \sum_{k=1}^{K} δ_k^{(L)} \cdot w_k^{(L)} \cdot f'(a_j^{(l)})`
- `K`：输出层节点数

3. 更新权重和偏置：`w_j^{(l)} = w_j^{(l)} - α \cdot δ_j^{(l)} \cdot a^{(l-1)}`
- `α`：学习率

### 2.2 MATLAB中BP神经网络的创建和训练

MATLAB提供了`feedforwardnet`函数创建BP神经网络。该函数需要指定网络结构（输入层、隐含层、输出层节点数）和训练参数（学习率、最大迭代次数）。

% 创建一个3层BP神经网络
net = feedforwardnet([10 20 10]);

% 设置训练参数
net.trainParam.lr = 0.01;
net.trainParam.epochs = 1000;

% 训练网络
net = train(net, inputs, targets);

### 2.3 BP神经网络的