Matlab主成分分析与奇异值分解：揭秘降维背后的数学奥秘

# 1. 主成分分析（PCA）简介**

主成分分析（PCA）是一种广泛应用于数据降维的统计技术。其核心思想是将高维数据投影到低维空间中，同时尽可能保留原始数据的关键信息。PCA通过识别数据中方差最大的方向（主成分），并沿这些方向投影数据，从而实现降维。

PCA在实践中有着广泛的应用，包括数据可视化、异常检测、模式识别和特征提取。通过减少数据维度，PCA可以简化数据处理，提高算法效率，并增强对数据的理解。

# 2. PCA的数学原理

### 2.1 线性代数基础

#### 2.1.1 向量和矩阵

**向量**

向量是具有大小和方向的有序元素集合。在数学中，向量通常用粗体小写字母表示，例如 **v**。向量的元素称为分量，分量可以是实数或复数。

**矩阵**

矩阵是按行和列排列的数字或符号的矩形阵列。在数学中，矩阵通常用大写字母表示，例如 **A**。矩阵的元素称为元素，元素可以是实数或复数。

#### 2.1.2 协方差矩阵

协方差矩阵是一个对称矩阵，其元素表示两个随机变量之间的协方差。协方差矩阵的第 (i, j) 个元素表示随机变量 X_i 和 X_j 之间的协方差。

协方差矩阵的数学定义如下：

Cov(X, Y) = E[(X - E[X])(Y - E[Y])]

其中：

* Cov(X, Y) 是 X 和 Y 之间的协方差
* E[X] 是 X 的期望值
* E[Y] 是 Y 的期望值

### 2.2 PCA的数学推导

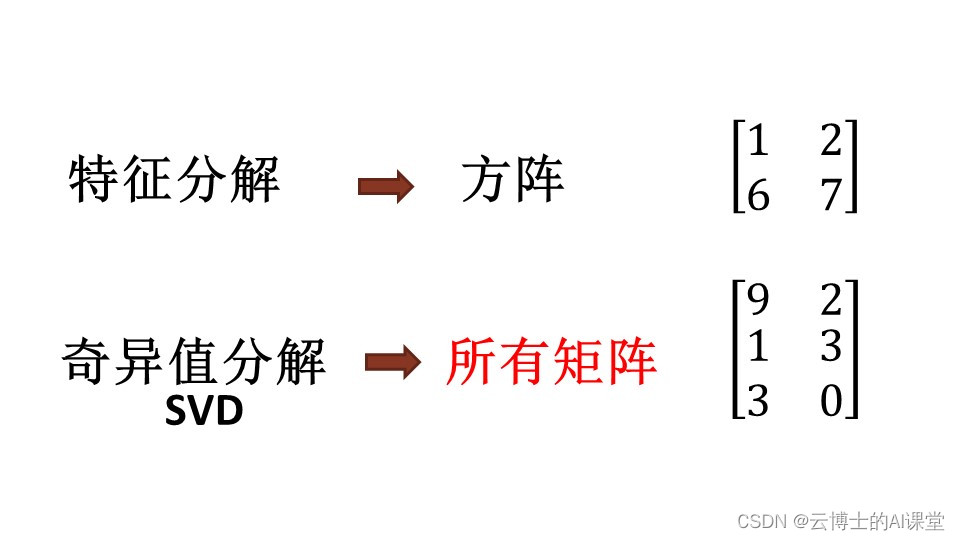
#### 2.2.1 特征值和特征向量

特征值和特征向量是线性代数中两个重要的概念。特征值是矩阵乘以其特征向量时得到的标量。特征向量是矩阵乘以其特征值时得到的向量。

特征值和特征向量可以用来对矩阵进行对角化。对角化是指将矩阵转换为一个对角矩阵，其中对角线上的元素是矩阵的特征值。

#### 2.2.2 降维原理

PCA 的基本思想是将原始数据投影到一个新的坐标系中，使得投影后的数据具有最大的方差。这个新的坐标系由原始数据协方差矩阵的特征向量组成。

PCA 的降维原理如下：

1. 计算原始数据协方差矩阵 **C**。
2. 计算 **C** 的特征值和特征向量。
3. 选择前 k 个特征值对应的特征向量，其中 k 是要降维到的维度。
4. 将原始数据投影到由这 k 个特征向量组成的子空间中。

投影后的数据将具有最大的方差，并且可以用于后续的分析或建模。

# 3. PCA在实践中的应用

### 3.1 数据预处理

在将PCA应用于实际数据集之前，通常需要进行数据预处理，以确保数据适合降维。数据预处理步骤包括：

#### 3.1.1 标准化和归一化

**标准化**将数据转换为均值为0、标准差为1的分布。这有助于消除不同特征量纲的不同影响，确保所有特征在降维过程中具有同等的重要性