Matlab主成分分析在数据挖掘中的应用：挖掘数据背后的黄金

# 1. 主成分分析（PCA）的基础**

主成分分析（PCA）是一种广泛用于数据挖掘和机器学习中的降维技术。它通过将原始数据投影到一个新的低维空间中，来减少数据的维度，同时尽可能保留原始数据的关键信息。

PCA的原理是找到原始数据中方差最大的线性组合，并将其作为主成分。这些主成分是原始数据的正交基，可以解释原始数据中最大的方差。通过选择前几个主成分，我们可以将原始数据降维到一个较低的维度，而不会丢失太多信息。

PCA在数据挖掘中具有广泛的应用，包括数据降维、数据可视化、异常检测和特征提取。它可以帮助我们从高维数据中提取有意义的信息，并简化数据分析和建模过程。

# 2. PCA在数据挖掘中的应用

PCA在数据挖掘中具有广泛的应用，主要体现在数据降维和数据可视化两个方面。

### 2.1 PCA用于数据降维

数据降维是将高维数据投影到低维空间的过程，目的是简化数据结构，降低计算复杂度。PCA是一种常用的数据降维方法，其原理是将原始数据投影到一个新的正交坐标系上，使得投影后的数据方差最大化。

#### 2.1.1 PCA的原理和算法

PCA的原理是基于协方差矩阵的特征分解。协方差矩阵是一个对称正定矩阵，其特征值和特征向量可以用来表示数据的方差和方向。PCA算法的步骤如下：

1. 计算原始数据的协方差矩阵。
2. 对协方差矩阵进行特征分解，得到特征值和特征向量。
3. 将特征值从大到小排序，选择前k个特征值对应的特征向量。
4. 将原始数据投影到这k个特征向量构成的子空间中，得到降维后的数据。

#### 2.1.2 PCA在高维数据降维中的应用

PCA在高维数据降维中的应用非常广泛，例如：

- **文本数据降维：**文本数据通常具有高维特征，PCA可以将其降维到低维空间，简化文本处理和分类任务。
- **图像数据降维：**图像数据也具有高维特征，PCA可以将其降维到低维空间，降低图像处理和识别任务的计算复杂度。
- **基因数据降维：**基因数据具有超高维特征，PCA可以将其降维到低维空间，简化基因分析和疾病诊断任务。

### 2.2 PCA用于数据可视化

数据可视化是将数据以图形化的方式呈现出来，以便于理解和分析。PCA可以将高维数据投影到低维空间中，从而实现数据可视化。

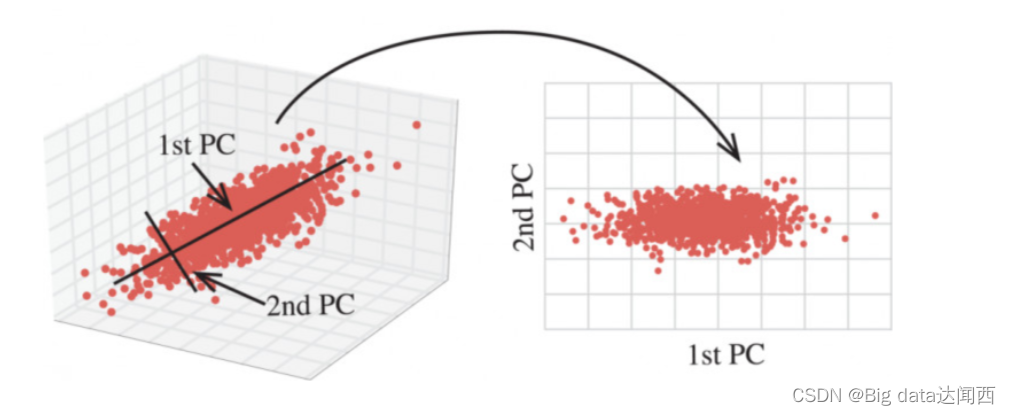
#### 2.2.1 PCA与主成分投影

主成分投影是PCA的一种应用，其目的是将高维数据投影到低维空间中，以便于可视化。主成分投影的步骤如下：

1. 计算原始数据的协方差矩阵。
2. 对协方差矩阵进行特征分解，得到特征值和特征向量。
3. 选择前k个特征值对应的特征向量，将原始数据投影到这k个特征向量构成的子空间中。
4. 将投影后的数据绘制成散点图或其他图形，进行可视化分析。

#### 2.2.2 PCA在数据可视化中的应用

PCA在数据可视化中的应用非常广泛，例如：

- **数据探索：**PCA可以将高维数据投影到低维空间中，从而帮助数据分析人员探索数据的分布和结构。
- **异常检测：**PCA可以将异常数据投影到低维空间中，使其与正常数据明显区分开来，从而实现异常检测。
- **模式识别：**PCA可以将不同模式的数据投影到低维空间中，使其在图形上形成不同的簇，从而实现模式识别。

# 3. MATLAB中PCA的实现

### 3.1 PCA函数的使用

#### 3.1.1 pca函数的语法和参数

MATLAB中提供了`pca`函数来实现主成分分析。其语法如下：

[coeff, score, latent, tsquared, explained, mu] = pca(X, numpc)

其中：

- `X`：输入数据矩阵，每一行表示一个样本，每一列表示一个特征。
- `numpc`：要提取的主成分数量（可选，默认为数据矩阵的列数）。
- `coeff`：主成分载荷矩阵，每一列表示一个主成分