Matlab主成分分析在金融领域的应用：风险评估与投资决策的利器

# 1. Matlab主成分分析概述

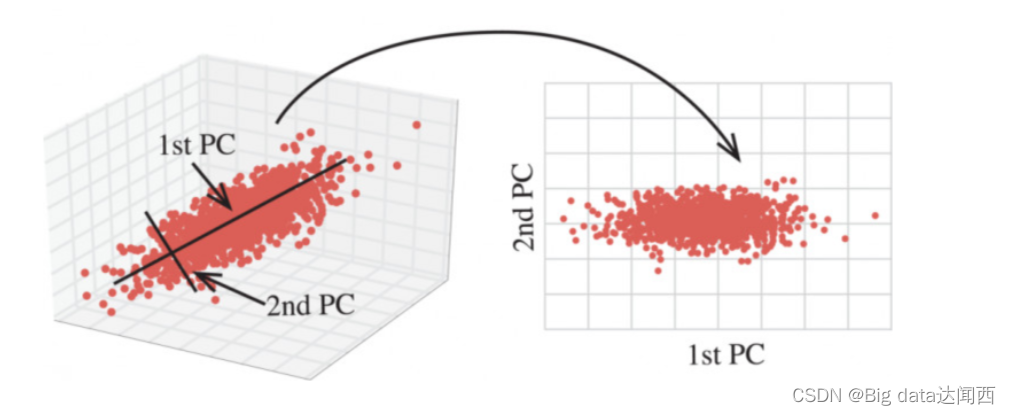
主成分分析（PCA）是一种广泛应用于金融领域的数据降维和特征提取技术。它通过线性变换将原始数据投影到一个新的正交空间，使得新空间中的前几个主成分包含了原始数据的大部分信息。

在金融风险评估中，PCA用于识别和提取影响金融风险的潜在因子。通过分析这些因子，可以建立风险评估模型，对金融风险进行量化和预测。在投资决策中，PCA用于构建投资组合，优化投资组合的风险和收益。通过提取和分析投资组合中的相关特征，可以构建多元化的投资组合，降低风险并提高收益。

# 2. 主成分分析在金融风险评估中的应用

### 2.1 主成分分析原理及金融风险度量

#### 2.1.1 主成分分析基本原理

主成分分析（PCA）是一种降维技术，用于将高维数据转换为低维数据，同时最大程度地保留原始数据的变异性。PCA通过以下步骤实现：

1. **数据中心化：**将原始数据减去其均值，使数据围绕原点分布。
2. **计算协方差矩阵：**计算数据集中每个特征对之间的协方差。
3. **求解特征值和特征向量：**对协方差矩阵进行特征分解，得到特征值和特征向量。
4. **选择主成分：**根据特征值从大到小排列，选择前几个特征值对应的特征向量作为主成分。

#### 2.1.2 金融风险度量的指标体系

金融风险度量指标体系包括：

* **流动性风险：**衡量资产变现能力，指标包括流动性比率、速动比率等。
* **市场风险：**衡量资产价格波动对投资组合的影响，指标包括贝塔系数、夏普比率等。
* **信用风险：**衡量债务人违约的可能性，指标包括违约率、信用评级等。
* **操作风险：**衡量内部流程和系统故障造成的损失，指标包括事件频率、损失严重程度等。

### 2.2 主成分分析在金融风险评估中的实践

#### 2.2.1 数据预处理和特征提取

* **数据预处理：**处理缺失值、异常值，标准化数据。
* **特征提取：**选择与金融风险相关的特征，如流动性比率、贝塔系数等。

#### 2.2.2 主成分提取和风险因子识别

* **主成分提取：**对预处理后的数据进行PCA，提取主成分。
* **风险因子识别：**主成分代表了数据中的主要变异性，可以作为金融风险因子。

#### 2.2.3 风险评估模型构建和验证

* **风险评估模型构建：**基于主成分和风险因子，构建风险评估模型。
* **模型验证：**使用历史数据验证模型的准确性和鲁棒性。

**代码块：**

% 数据预处理
data = preprocess(data);

% 主成分提取
[coeff, score, latent] = pca(data);

% 风险因子识别
risk_factors = coeff(:, 1:2);  % 选择前两个主成分作为风险因子

% 风险评估模型构建
model = fitlm(score, 'ResponseVariable', 'RiskLevel');

% 模型验证
accuracy = crossval('accuracy', model, 10);

**代码逻辑逐行解读：**

* `preprocess`函数对数据进行预处理，包括缺失值处理、异常值处理和标准化。
* `pca`函数进行PCA，返回主成分系数矩阵`coeff`、主成分得分矩阵`score`和特征值向量`latent`。
* 选择前两个主成分作为风险因子，因为它们代表了数据中最大的变异性。
* `fitlm`函数构建线性回归模型，以主成分得分作为自变量，风险等级作为因变量。
* `crossval`函数进行交叉验证，计算模型的准确性。

# 3.1 主成分分析原理及投资组合优化

**3.1.1 主成分分析基本原理**

主成分分析（PCA）是一种降维技术，用于将高维数据投影到低维空间中，同时保留数据的最大方